114. 도시 분할 계획

• 마을은 N개의 집과 그 집들을 연결하는 M개의 길로 이루어져 있다.

  • 길은 어느 방향으로든지 다닐 수 있는 편리한 길이다.

  • 그리고 길마다 길을 유지하는데 드는 유지비가 있다.

• 마을 이장은 마을을 2개의 분리된 마을로 분할할 계획을 세우고 있다.

  • 마을을 분할할 때는 각 분리된 마을 아네 집들이 서로 연결되도록 분할해야 한다.

    • 분리된 마을 안에 있는 임의의 두 집 사이에 경로가 항상 존재해야 한다는 뜻이다.

  • 마을에는 집이 하나 이상 있어야 한다.

• 일단 분리된 두 마을 사잉 있는 길들은 필요가 없으므로 없앨 수 있다.

  • 각 분리된 마을 안에서도 임의의 두 집 사이에 경로가 항상 존재하게 하면서 기을 더 없앨 수 있다.

• 마을의 이장은 위 조건을 만족하도록 길들을 모두 없애고 나머지 길의 유지비의 합을 최소로 하고 싶다.

  • 이것을 구하는 프로그램을 작성하시오.

• 입력조건

  • 첫째 줄에 집의 개수 N, 길의 개수M이 주어진다. N은 2 이상 100,000 이하인 정수이고, M은 1 이상 1,000,000 이하인 정수이다.

  • 그 다음 줄부터 M줄에 걸쳐 기르이 정보가 A, B, C 3개의 정수로 공백으로 구분되어 주어진는데, A번 집과 B번 집을 연결하는 길의 유지비가 C(1 ≤ C ≤ 1,000)라는 뜻이다.

• 출력조건

  • 첫째 줄에 길을 없애고 남은 유지비 합의 최솟값을 출력한다.

1. 크루스칼 알고리즘(최소 신장 트리)를 이용한 풀이

def find_parent(parent, x):
  if parent[x] != x:
    parent[x] = find_parent(parent, parent[x])
  return parent[x]

def union_parent(parent, a, b):
  a = find_parent(parent, a)
  b = find_parent(parent, b)

  if a < b:
    parent[b] = a
  else:
    parent[a] = b

v, e = map(int, input().split())
parent = [0] * (v + 1)

#모든 간선을 담을 리스트와 최종 비용을 담을 변수
edges = []
result = 0

for i in range(1, v + 1):
  parent[i] = i

for _ in range(e):
  a, b, cost = map(int, input().split())
  edges.append((cost, a, b)) #정렬을 위해 첫번째 원소 비용으로

#간선을 비용순으로 정렬
edges.sort()
last = 0 #최소 신장 트리에 포함되는 간선중에서 가장 비용이 큰 간선 ★

for edge in edges:
  cost, a, b = edge
  #사이클이 발생하지 않는 경우에만 집합에 포함
  if find_parent(parent, a) != find_parent(parent, b):
    union_parent(parent, a, b)
    result += cost
    last = cost #정렬되었기에 결국 마지막의 가장 큰 값이 들어가게 된다


print(result - last) #가장 비용이 큰 간선 제거
  

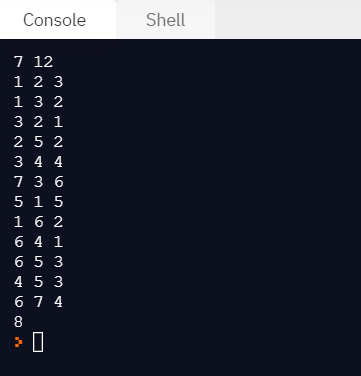
• 전체의 그래프에서 2개의 최소 신장 트리를 만들어야 한다.

  • 가장 간단한 방법은 크루스칼 알고리즘으로 최소 신장 트리를 찾은 뒤에 최소 신장 트리를 구성하는 간선 중에서 가장 비용이 큰 간선을 제거하는 것이다.

  • 그러면 최소 신장 트리가 2개의 부분 그래프로 나누어지며, 문제에서 요구하는 최적의 해를 만족한다.

2. C++ 코드

#include <bits/stdc++.h>

using namespace std;

// 노드의 개수와 간선(Union 연산)의 개수 입력받기
int v, e;
int parent[100001]; // 부모 테이블 초기화
// 모든 간선을 담을 리스트와, 최종 비용을 담을 변수
vector<pair<int, pair<int, int> > > edges;
int result = 0;

// 특정 원소가 속한 집합을 찾기
int findParent(int x) {
    // 루트 노드가 아니라면, 루트 노드를 찾을 때까지 재귀적으로 호출
    if (x == parent[x]) return x;
    return parent[x] = findParent(parent[x]);
}

// 두 원소가 속한 집합을 합치기
void unionParent(int a, int b) {
    a = findParent(a);
    b = findParent(b);
    if (a < b) parent[b] = a;
    else parent[a] = b;
}

int main(void) {
    cin >> v >> e;

    // 부모 테이블상에서, 부모를 자기 자신으로 초기화
    for (int i = 1; i <= v; i++) {
        parent[i] = i;
    }

    // 모든 간선에 대한 정보를 입력 받기
    for (int i = 0; i < e; i++) {
        int a, b, cost;
        cin >> a >> b >> cost;
        // 비용순으로 정렬하기 위해서 튜플의 첫 번째 원소를 비용으로 설정
        edges.push_back({cost, {a, b}});
    }

    // 간선을 비용순으로 정렬
    sort(edges.begin(), edges.end());
    int last = 0; // 최소 신장 트리에 포함되는 간선 중에서 가장 비용이 큰 간선

    // 간선을 하나씩 확인하며
    for (int i = 0; i < edges.size(); i++) {
        int cost = edges[i].first;
        int a = edges[i].second.first;
        int b = edges[i].second.second;
        // 사이클이 발생하지 않는 경우에만 집합에 포함
        if (findParent(a) != findParent(b)) {
            unionParent(a, b);
            result += cost;
            last = cost;
        }
    }

    cout << result - last << '\n';
}

3. Java 코드

import java.util.*;

class Edge implements Comparable<Edge> {

    private int distance;
    private int nodeA;
    private int nodeB;

    public Edge(int distance, int nodeA, int nodeB) {
        this.distance = distance;
        this.nodeA = nodeA;
        this.nodeB = nodeB;
    }

    public int getDistance() {
        return this.distance;
    }

    public int getNodeA() {
        return this.nodeA;
    }

    public int getNodeB() {
        return this.nodeB;
    }

    // 거리(비용)가 짧은 것이 높은 우선순위를 가지도록 설정
    @Override
    public int compareTo(Edge other) {
        if (this.distance < other.distance) {
            return -1;
        }
        return 1;
    }
}

public class Main {

    // 노드의 개수(V)와 간선(Union 연산)의 개수(E)
    public static int v, e;
    public static int[] parent = new int[100001]; // 부모 테이블 초기화
    // 모든 간선을 담을 리스트와, 최종 비용을 담을 변수
    public static ArrayList<Edge> edges = new ArrayList<>();
    public static int result = 0;

    // 특정 원소가 속한 집합을 찾기
    public static int findParent(int x) {
        // 루트 노드가 아니라면, 루트 노드를 찾을 때까지 재귀적으로 호출
        if (x == parent[x]) return x;
        return parent[x] = findParent(parent[x]);
    }

    // 두 원소가 속한 집합을 합치기
    public static void unionParent(int a, int b) {
        a = findParent(a);
        b = findParent(b);
        if (a < b) parent[b] = a;
        else parent[a] = b;
    }

    public static void main(String[] args) {
        Scanner sc = new Scanner(System.in);

        v = sc.nextInt();
        e = sc.nextInt();

        // 부모 테이블상에서, 부모를 자기 자신으로 초기화
        for (int i = 1; i <= v; i++) {
            parent[i] = i;
        }

        // 모든 간선에 대한 정보를 입력 받기
        for (int i = 0; i < e; i++) {
            int a = sc.nextInt();
            int b = sc.nextInt();
            int cost = sc.nextInt();
            // 비용순으로 정렬하기 위해서 튜플의 첫 번째 원소를 비용으로 설정
            edges.add(new Edge(cost, a, b));
        }

        // 간선을 비용순으로 정렬
        Collections.sort(edges);
        int last = 0; // 최소 신장 트리에 포함되는 간선 중에서 가장 비용이 큰 간선

        // 간선을 하나씩 확인하며
        for (int i = 0; i < edges.size(); i++) {
            int cost = edges.get(i).getDistance();
            int a = edges.get(i).getNodeA();
            int b = edges.get(i).getNodeB();
            // 사이클이 발생하지 않는 경우에만 집합에 포함
            if (findParent(a) != findParent(b)) {
                unionParent(a, b);
                result += cost;
                last = cost;
            }
        }

        System.out.println(result - last);
    }
}