- 연결 리스트가 팰린드롬 구조인지 판별하라
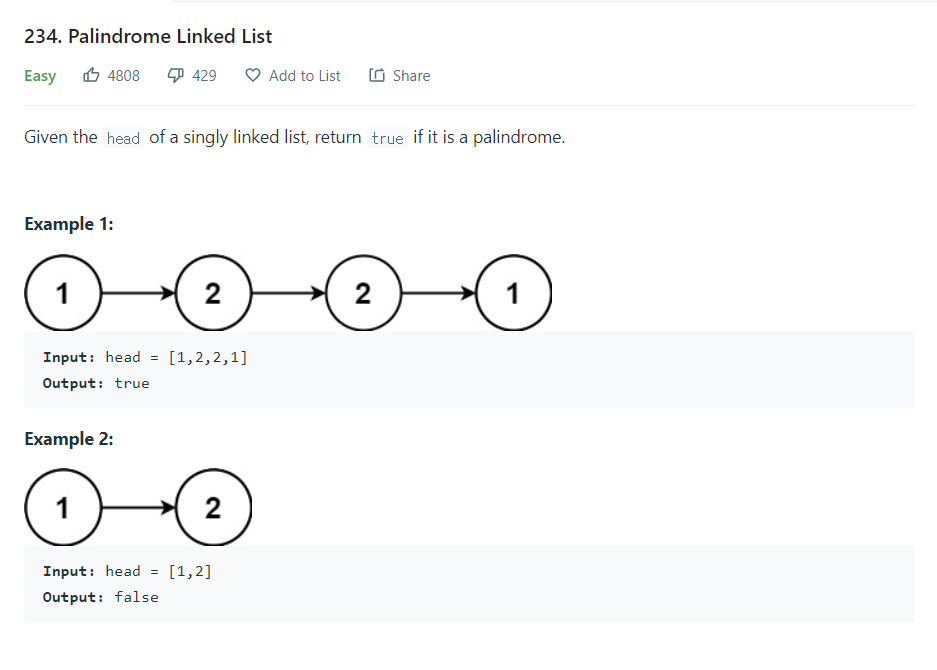

1. 리스트 변환
# Definition for singly-linked list.
# class ListNode:
# def __init__(self, val=0, next=None):
# self.val = val
# self.next = next
class Solution:
def isPalindrome(self, head: ListNode) -> bool:
q: List = []
if not head:
return True
node = head
#리스트 변환
while node is not None:
q.append(node.val)
node = node.next
#팰린드롬 판별
while len(q) > 1:
if q.pop(0) != q.pop():
return False
return True-
파이썬의 리스트는 q.pop(0) != q.pop() 형태로 얼마든지 인덱스를 지정해서 비교가 가능하기 때문에 이 문제는 리스트만으로도 충분히 풀이가 가능하다.
- q.pop(0)과 같이 동적 배열로 구성된 리스트는 맨 앞 아이템을 가져오기에 적합한 자료형이 아니다.
- 첫번째 값을 꺼내오면 모든 값이 한 칸씩 시프팅(Shifting)되며, 시간 복잡도 O(n)이 발생하기 때문이다.
- 하지만, 연결 리스트 자료형을 변환하지 않고 풀이를 해보자
2. 데크를 이용한 최적화
# Definition for singly-linked list.
# class ListNode:
# def __init__(self, val=0, next=None):
# self.val = val
# self.next = next
class Solution:
def isPalindrome(self, head: ListNode) -> bool:
#데크 자료형 선언
q: Deque = collections.deque()
if not head:
return True
node = head
#리스트 변환
while node is not None:
q.append(node.val)
node = node.next
#팰린드롬 판별
while len(q) > 1:
if q.popleft() != q.pop():
return False
return True-
파이썬의 데크(Deque) 는 이중 연결 리스트 구조로 양쪽 방향 모두 추출하는 데 시간 복잡도 O(1)에 실행된다.
-
파이썬에서 리스트를 데크로 수정하려면 딱 두 군데만 수정하면 되기 때문에 무척 쉽게 변경할 수 있다.
- 이를 통해 앞의 풀이보다 2배 이상 빨라지는 효과가 있다.
q: Deque = collections.deque()
...
if q.popleft() != q.pop():
...
3. 고(Go)를 이용한 데크 구현
-
고는 데크 자료형을 지원하지 않기에 (외부라이브러리 제외) 직접 구현하는 방법 밖에는 없다. (100줄 이상)
-
시간 제한이 있는 코딩 테스트에서 이처럼 외부 코드를 가져오는 일은 생산성이 매우 떨어진다. 뿐만 아니라 문제가 없도록 일일이 확인하는 과정은 매우 위험하고 비효율적이다.
-
But, 바닥부터 고로 구현한 경우 성능이 매우 좋아서 파이썬 대비 약 5배 가까이 더 빠른 속도를 보인다는 점이다.
4. 런너를 이용한 우아한 풀이 ⭐
# Definition for singly-linked list.
# class ListNode:
# def __init__(self, val=0, next=None):
# self.val = val
# self.next = next
class Solution:
def isPalindrome(self, head: ListNode) -> bool:
rev = None
slow = fast = head
#런너를 이용해 역순 연결 리스트 구성
while fast and fast.next:
fast = fast.next.next
rev, rev.next, slow = slow, rev, slow.next
if fast:
slow = slow.next
#팰린드롬 여부 확인
while rev and rev.val == slow.val:
slow, rev = slow.next, rev.next
return not rev-
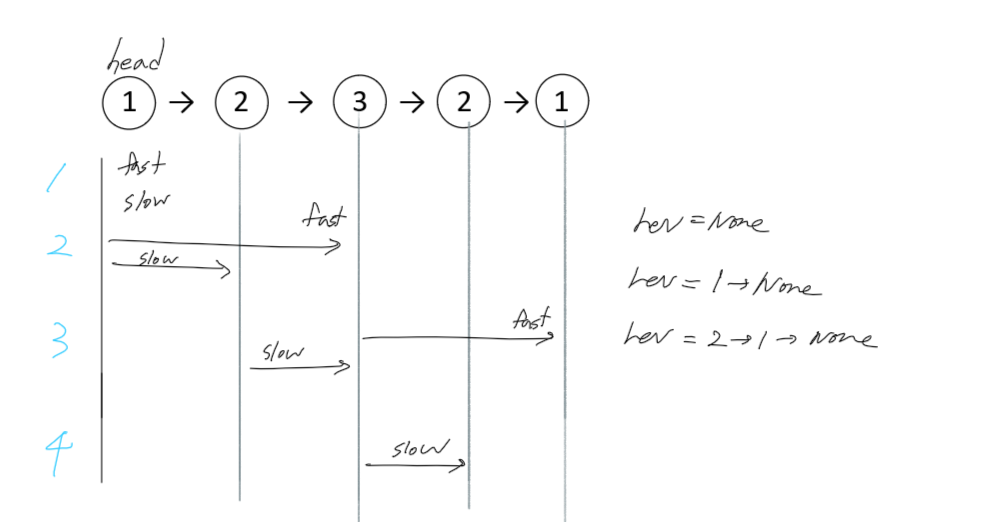
그림에서 파란색으로 표시된 번호 1,2,3,4는 실행 순서를 보여준다.
-
순서에 따라 2개의 런너, 즉 빠른 런너(Fast Runner)와 느린 런너(Slow Runner)를 각각 출발 시키면 빠른 런너가 끝에 다다를 때 느린 런너는 정확히 중간 지점에 도달하게 될 것이다.
-
느린 런너는 중간까지 이동하면서 역순으로 연결 리스트 rev를 만들어 나간다.
-
이제 중간에 도달한 느린 런너가 나머지 경로를 이동할 때, 역순으로 만든 연결 리스트의 값들과 일치하는지 확인해나가면 된다.
-
-
빠른 런너 fast와 느린 런너 slow의 초깃값은 다음과 같이 모두 head에서 시작한다.
-
이제 next가 존재하지 않을 때까지 이동한다.
-
빠른 런너 fast는 두 칸씩, 느린 런너 slow는 한 칸씩 이동한다.
-
그러면서 역순으로 연결 리스트 rev를 생성하는 로직을 slow 앞에 덧붙인다.
-
첫 rev의 값은 None에서 시작되고, 런너가 이동하면서 1 -> None, 2 -> 1 -> None로 점점 이전 값으로 연결되는 구조가 된다.
-
-
다중할당
rev, rev.next, slow = slow, rev, slow.next- 역순 연결리스트는 현재 값을 slow로 교체하고 rev.next는 rev가 된다.
- 즉 앞에 계속 새로운 노드가 추가되는 형태가 된다. 결국 이 연결리스트는 slow의 역순 연결 리스트가 될 것이다.
- 입력 값이 홀수일 때와 짝수일 때 마지막 처리가 다른데, 홀수 일 때는 slow 런너가 한 칸 더 앞으로 이동하여 중앙의 값을 빗겨 나가야 한다.
- 여기서 2은 중앙에 위치한 값으로, 팰린드롬 체크에서 배제되어야 하기 때문이다. 이는 fast가 아직 None이 아니라는 경우로 간주할 수 있으며, 따라서 이 경우 다음과 같이 slow를 한 칸 더 이동해 마무리한다.
-
팰린드롬 여부 확인
-
역순으로 만든 연결 리스트 rev를 반복한다.
-
slow의 나머지 이동 경로와 역순으로 만든 rev의 노드를 하나씩 풀어가면서 비교한다.
-
정산적으로 비교가 종료됐다면 slow와 rev가 모두 끝까지 이동해 둘 다 None이 될 것이다.
-
최종 결과는 return not rev 도는 return not slow 모두 가능하다.
-
➕ 런너(Runner) 기법
-
연결 리스트를 순회할 때 2개의 포인터를 동시에 사용하는 기법
-
한 포인터가 다른 포인터보다 앞서게 하여 병합 지점이나 중간 위치, 길이 등을 판별할 때 유용하게 사용할 수 있다.
-
대개 빠른 런너는 두 칸씩, 느린 런너는 한 칸씩 이동하게 된다.
이 때 빠른 런너가 연결 리스트의 끝에 도달하면, 느린 런너는 정확히 연결 리스트의 중간 지점을 가리키게 된다. -
중간 위치를 찾아내면, 여기서부터 값을 비교하거나 뒤집기를 시도하는 등 여러모로 활용할 수 있기에, 연결 리스트 문제에서는 반드시 쓰이는 기법이기도 하다.
