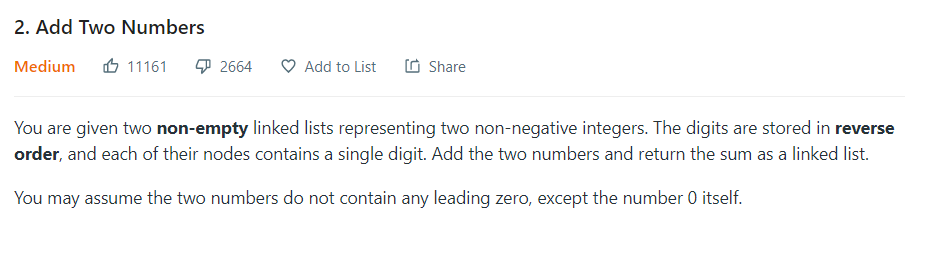
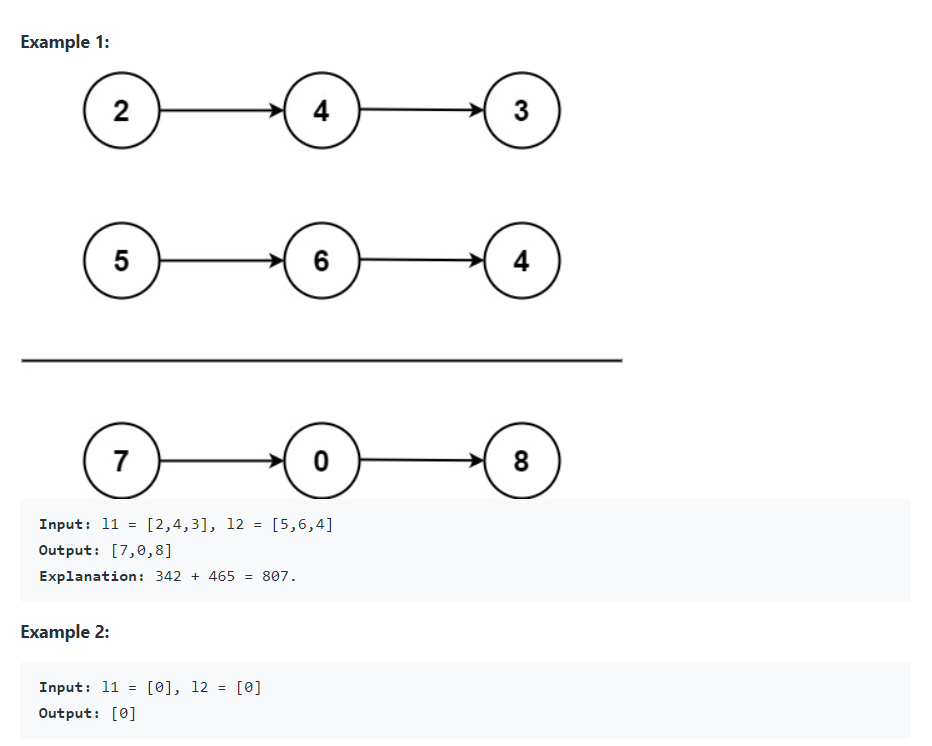
- 역순으로 저장된 연결 리스트의 숫자를 더하라

1. 자료형 변환 (76ms)
# Definition for singly-linked list.
# class ListNode:
# def __init__(self, val=0, next=None):
# self.val = val
# self.next = next
class Solution:
def reverseList(self, head:ListNode) -> ListNode:
node, prev = head, None
while node:
next, node.next = node.next, prev
prev, node = node, next
return prev
#연결 리스트를 파이썬 리스트로 변환
def toList(self, node: ListNode) -> ListNode:
list: List = []
while node:
list.append(node.val)
node = node.next
return list
#파이썬 리스트를 연결 리스트로 변환
def toReversedLinkedList(self, result: ListNode) -> ListNode:
prev: ListNode = None
for r in result:
node = ListNode(r)
node.next = prev
prev = node
return node
#두 연결 리스트의 덧셈
def addTwoNumbers(self, l1:ListNode, l2:ListNode) -> ListNode:
a = self.toList(self.reverseList(l1))
b = self.toList(self.reverseList(l2))
resultStr = int(''.join(str(e) for e in a)) + \
int(''.join(str(e) for e in b))
#최종 계산 결과 연결 리스트 변환
return self.toReversedLinkedList(str(resultStr))
-
먼저, 역순으로 된 연결리스트를 뒤집어야 한다.
- 반복을 통해 뒤집는다
-
다음으로 덧셈 연산을 위해 연결 리스트를 파이썬의 리스트로 변경한다.
- 위 코드는 node를 반복하며 값을 리스트에 추가하는 함수를 사용하였다.
-
리스트를 다시 연결 리스트로 변경한다.
-
여기서는 순서대로 엮어 나가는 방식으로 구현했는데, 이렇게 하면 뒤집힌 연결 리스트가 된다.
-
이 문제에서는 출력 또한 역순으로 하도록 요구하고 있기에 이 상태 그대로 내보내면 된다.
-
다시 뒤집어야 한다면 위의 함수에 다시 대입하면 된다.
-
-
이제 덧셈 연산을 하면 되는데, 이를 위해서는 리스트를 int 형태로 결합해야 한다.
-
이전에 문자열 리스트를 str으로 면경하는 과정을 살펴본 바 있다.
''.join(s)와 같은 형식으로 처리가 가능하다. -
여기서는
str(e)로 각 항목을 문자로 변경한 다음join()으로 합쳤다. -
또한 , 덧셈 연산을 위해서 int로 다시 변경해주어야 한다.
-
resultStr = int(''.join(str(e) for e in a)) + \
int(''.join(str(e) for e in b))
-
마지막으로, 최종 계산 결과를 연결 리스트로 바꿔준다.
-
toReversedLinkedList()를 사용하면 쉽게 변환할 수 있다. -
단, 여기서는 문자열을 입력값으로 받기 때문에 다음과 같이
str()으로 한 번 변환하는 작업이 필요하다
-
return self.toReversedLinkedList(str(resultStr))2. 전가산기 구현 (88ms)
논리 회로의 전가산기(Full Adder)과 유사한 형태를 구현해보자
- 이진법이 아니라 십진법이라는 차이만 있을 뿐, 자리 올림수(Carry)를 구하는 것까지 가산기의 원리와 거의 동일하다.
<전가산기 진리표(Truth Table)>
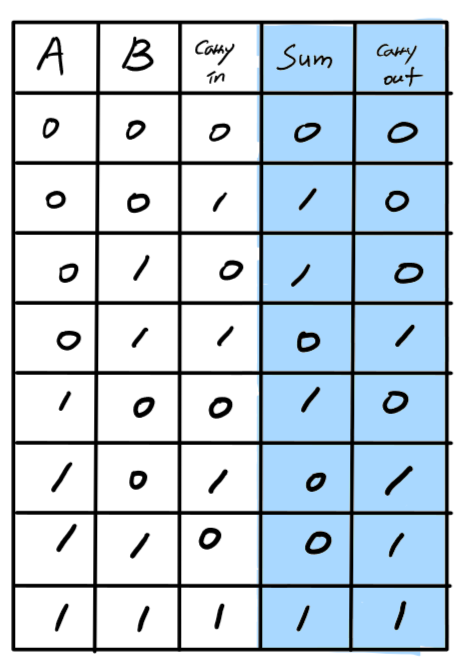
- 입력값 A와 B, 이전의 자리올림스(Carry in) 이렇게 3가지 입력으로 합(Sum)과 다음 자리올림수(Carry out) 여부를 결정한다.
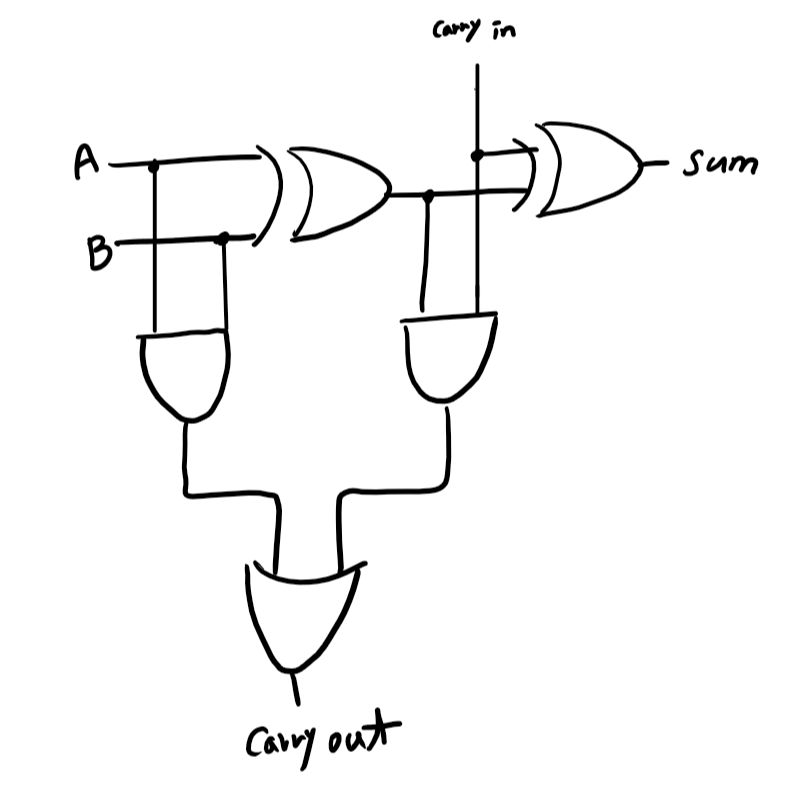
<전가산기 회로도>
-
입력값 A, B는 오른쪽으로는 XOR 게이트를 통과한 결과가 나아가고, 아래로는 AND 게이트를 통과한 결과가 나아간다.
-
그렇게 함과 다음 자리올리수 위치에 도달한 결과가 진리표이다.
-
실제로 덧셈연산을 수행하는 논리회로의 원리며, 산술 논리 장치(Arithmetic Logic Unit)를 구성하는 디지털 회로의 일부분이다.
- 산술 논리 장치는 컴퓨터의 중앙 처리 장치, 그러니까 우리가 잘 아는 CPU의 한 부분이기도 하다.
# Definition for singly-linked list.
# class ListNode:
# def __init__(self, val=0, next=None):
# self.val = val
# self.next = next
class Solution:
def addTwoNumbers(self, l1:ListNode, l2:ListNode) -> ListNode:
root = head = ListNode(0)
carry = 0
while l1 or l1 or carry:
sum = 0
#두 입력값의 합 계산
if l1:
sum += l1.val
l1 = l1.next
if l2:
sum += l2.val
l2 = l2.next
# 몫(자리올림수)과 나머지(값) 계산
# carry = sum + carry // 10
# val = sum + carry % 10
carry, val = divmod(sum + carry, 10)
head.next = ListNode(val)
head = head.next
return root.next-
연산 결과로 나머지(Remainder) 를 취하고 몫(Quotient) 은 자리 올림수 형태로 올리는 전가산기의 전체적인 구조만 참고해 풀이한다.
-
l1, l2는 전가산기 회로도에서 A, B의 역할과 동일하다. 두 입력값의 연산을 수행하고 다음과 같이 자릿수가 넘어갈 경우에는 자리 올리수를 설정할 것이다.
carry, val = divmod(sum + carry, 10) -
divmod( )는 파이썬의 내장 함수로, 몫과 나머지로 구성된 튜플을 리턴한다.
- 즉, (a//b, a%b)와 동일한 결과를 출력한다.
-
divmod의 결과로, 가산 결과가 두 자릿수가 될 경우, 몫은 자리올림수로 설정해 다음번 연산에 사용되게 하고, 나머지는 값으로 취한다.
-
다음으로 이 값을 연결 리스트로 만들어주면 된다.
-
원래 가산기는 논리 회로를 이용해 이진 연산을 수행하지만 여기서는 전체적인 구조만 참고하여 십진 연산에 응용해봤다.
