171. 산책

백준

1. Python

2. C++

#include<bits/stdc++.h>
using namespace std;

int A[1010][1010];
int dp[1010][1010];
int main(void) {
	ios::sync_with_stdio(false); cin.tie(nullptr); cout.tie(nullptr);
	int h, w, n; cin >> h >> w >> n;
	for (int i = 1; i <= h; i++) {
		for (int j = 1; j <= w; j++) {
			cin >> A[i][j];
		}
	}
	dp[1][1] = n - 1;
	for (int i = 1; i <= h; i++) {
		for (int j = 1; j <= w; j++) {
			if (i > 1) dp[i][j] += (A[i - 1][j] == 0 ? (dp[i - 1][j] + 1) / 2 : dp[i - 1][j] / 2);
			if (j > 1) dp[i][j] += (A[i][j - 1] == 1 ? (dp[i][j - 1] + 1) / 2 : dp[i][j - 1] / 2);
		}
	}
	int x = 1, y = 1;
	while (x <= h && y <= w) {
		if ((A[x][y] + dp[x][y]) % 2) y++;
		else x++;
	}
	cout << x << ' ' << y << '\n';
}
 



출처: https://rebro.kr/142 [Rebro의 코딩 일기장]

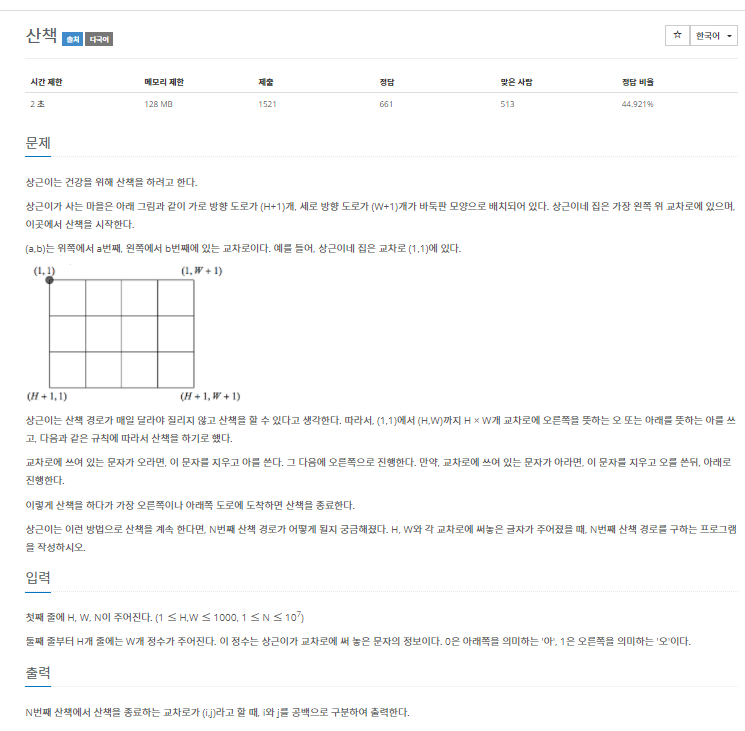
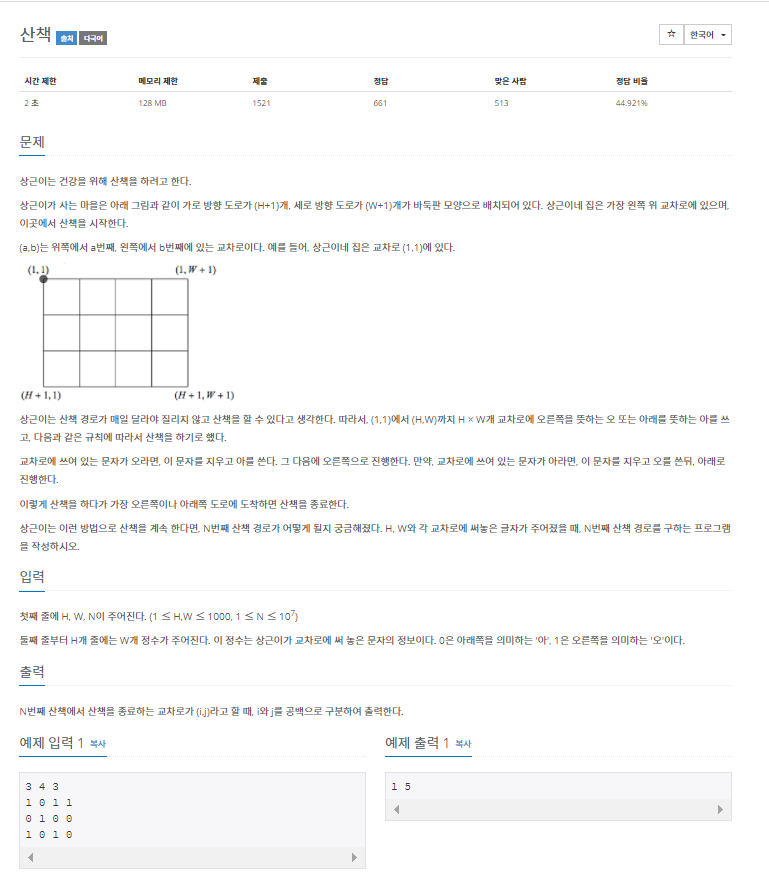
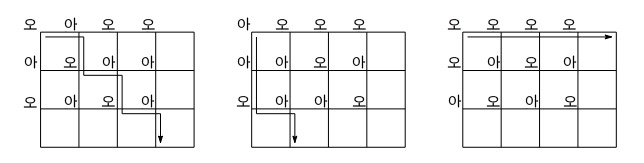
• 산책로의 밖으로 나가면 산책이 종료되고, 한번 교차로를 지나면 해당 교차로의 방향은 반대가 된다. 즉, 오른쪽이었으면 아래쪽으로, 아래쪽이었으면 오른쪽으로 바뀐다.

• N-1번의 산책이 끝난 후, N번째 산책을 할 때 산책이 종료되었을 때의 위치를 하는 문제이다. (N = 10^7)

• 교차로의 방향은 해당 교차로를 몇 번 방문했는지에 따라서 달라지므로 N번째 산책 이전까지 각 교차로의 방문 횟수를 구하면 N번째 산책의 도착지점을 알 수 있다.

  • 따라서, dp table을 dp[i][j] = 교차로 (i, j)를 방문한 횟수로 정의한다.

• (1, 1)은 시작점이므로 항상 방문하기 때문에 dp[i][j] = N-1이다.

  • 현재 위치를 (x, y)라고 하면, 항상 오른쪽 또는 아래쪽으로 이동하기 때문에 (x-1, y)와 (x, y-1)만 체크하면 된다.

• (x-1, y)의 초깃값을 0이라고 하고, (x-1, y)를 k번 방문했다고 가정하자. 그러면 (x-1, y)에서 (x, y)로 (k+1)/2번 이동할 것이다.

  • 반대로 (x-1, y)의 초깃값을 1이라고 하면 (x-1, y)에서 (x, y)로 k/2번 이동할 것이다.

• 즉, 초기 방향에 따라서 더해지는 값이 달라지게 되는 것이다.

• 최종적으로 N번째 산책하기 전의 교차로의 상태를 만들어둔 다음 N번째는 직접 이동시켜서 도착점을 찾아주면 된다.