-
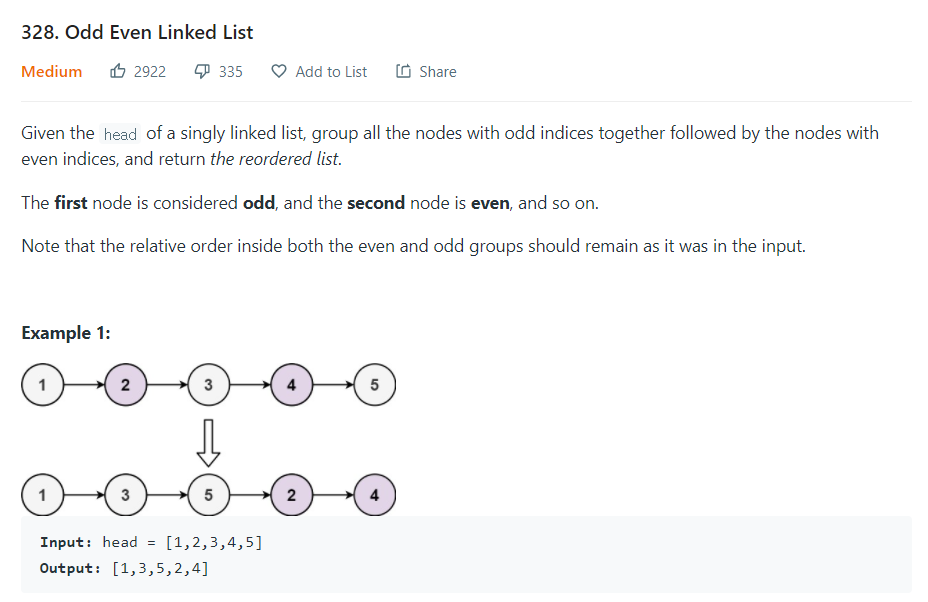
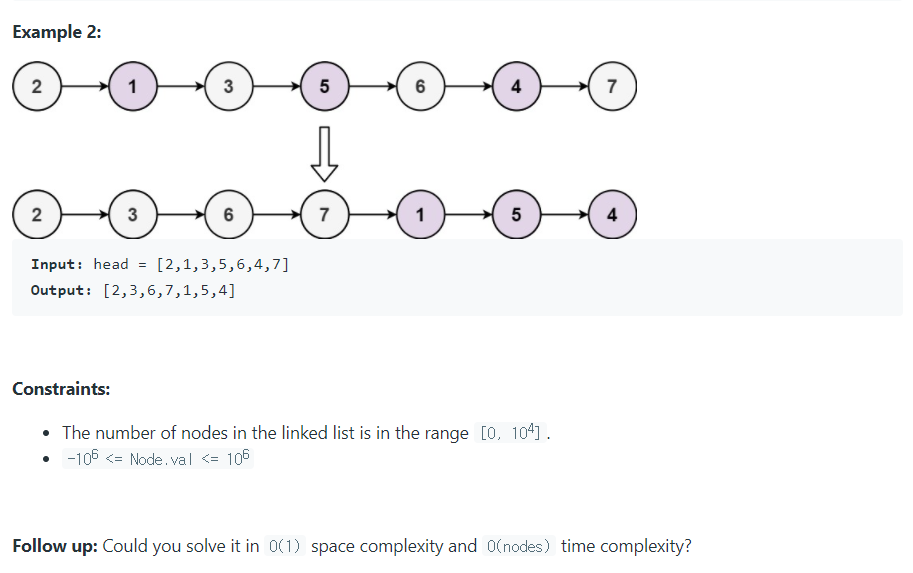
연결 리스트를 홀수 노드 다음에 짝수 노드가 오도록 재구성하라.
-
공간 복잡도 O(1), 시간 복잡도 O(n)에 풀이하라
1. 반복 구조로 홀짝 노드 처리
# Definition for singly-linked list.
# class ListNode:
# def __init__(self, val=0, next=None):
# self.val = val
# self.next = next
class Solution:
def oddEvenList(self, head: ListNode) -> ListNode:
#예외 처리
if head is None:
return None
odd = head
even = head.next
even_head = head.next
#반복하면서 홀짝 노드 처리
while even and even.next:
odd.next, even.next = odd.next.next, even.next.next
odd, even = odd.next, even.next
#홀수노드의 마지막을 짝수 헤드로 연결
odd.next = even_head
return head
-
이런 문제는 제약이 없을 경우 연결 리스트를 리스트로 바꾸고 파이썬 리스트가 제공하는 슬라이싱과 같은 다양한 함수를 사용하면 좀 더 쉽고 직관적이며 또한 빠르게 풀 수 있다.
-
파이썬 내장 함수의 실행 속도가 훨씬 더 빠르기 때문이다.
-
But, 이러한 풀이 방식은 우아하지 않다.
-
-
홀(odd), 짝(even) 각 노드를 구성한 다음 홀수 노드의 마지막을 짝수 노드의 처음과 이어주면 될 것 같다.
-
입력 값을 다음과 같이 생각해보자.
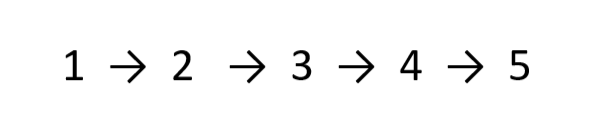
-
홀수 변수는 head이고, 짝수 변수는 head.next이다.
- 짝수의 헤드는 head.next이므로, even_head = even = head.next로 일단 시작한다.
-
while을 통해서 루프를 돌면서 처리한다.
-
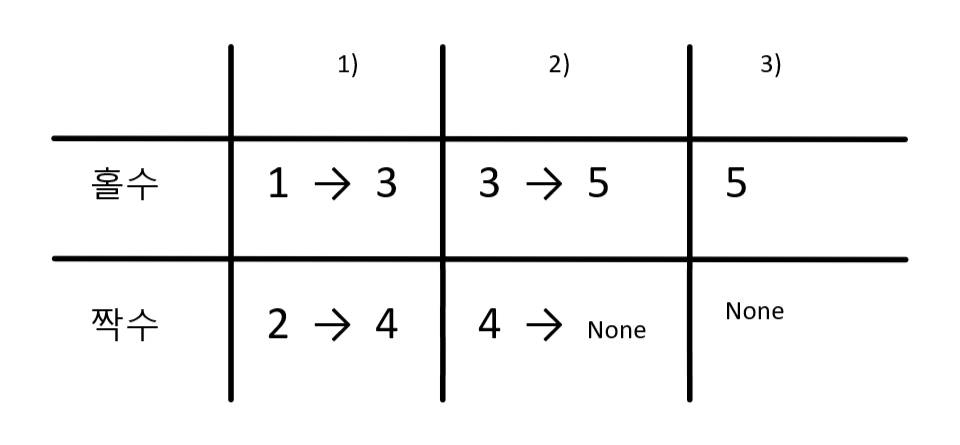
첫 번째 반복 시 홀수 odd는 1 -> 3으로 연결되고, 3을 값으로 갖게 된다.
짝수 even은 2->4가 되고, 4를 값으로 갖는다. -
두 번째는 3->5와 4->None이 되고, 마지막으로 5와 None이 남게 된다.
-
-
다중할당
odd.next, odd = odd.next.next, odd.next-
아쉽게도 가능하지 않다.
-
첫 번째 반복의 경우 1->3이 되지만 odd는 2가 된다. 아직 odd는 head는 동일한 참조며, head.next가 2이기 때문이다.
-
기대하는 결과는 1->3이 되고 odd가 3이되는 것인데, 이처럼 다중할당으로 처리하게 되면 서로 다른 결과가 된다.
-
다만, 홀짝처리를 하나로 묶어서 다음과 같이 두 줄로 처리하는 다중 할당은 가능하다.
odd.next, even.next = odd.next.next, even.next.next odd, even = odd.next, even.next- 이렇게 해서 끝까지 처리되면 홀수 odd는 5, 짝수 even은 None이 된다.
-
-
이제 odd.next를 짝수의 헤드 even_head와 연결한다.
-
그리고 head를 리턴한다
-
head는 1, even_head는 2가 되기 때문에, 앞서 처리된 내용을 바탕으로 1부터 결과를 쭉 나열해보면 1->3->5->2->4->None이 된다.
-
odd, even, even_head 등의 변수들은 n의 크기에 관계 없이 항상 일정하게 사용하기 때문에, 공간 복잡도 또한 O(1)으로 제약 조건을 만족한다.