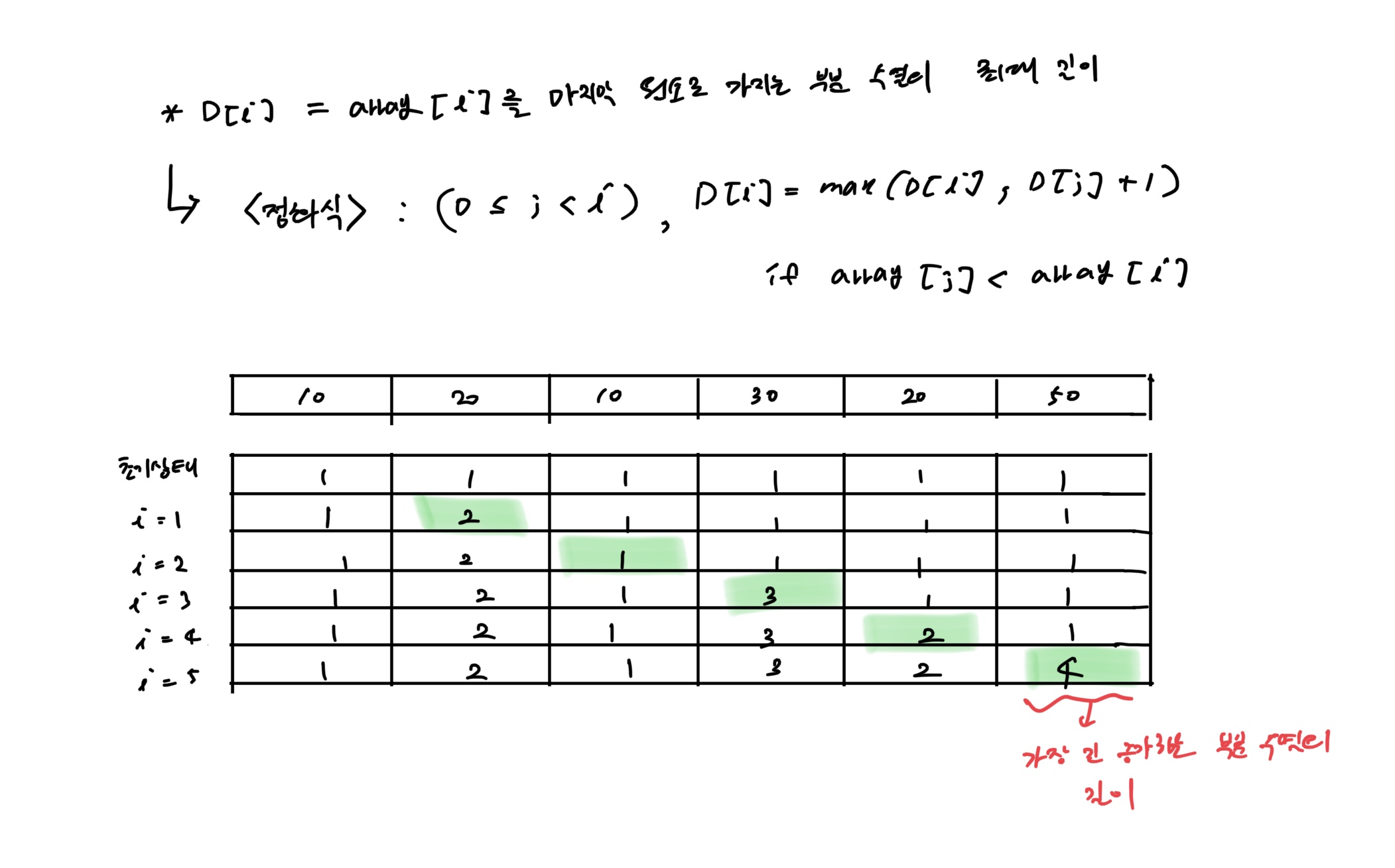
가장 긴 증가하는 부분 수열 (LIS, Longest Increasing Subsequence)
- 하나의 수열이 주어졌을 때 값들이 증가하는 형태의 가장 긴 부분 수열을 찾는 문제
import sys
input = sys.stdin.readline
n = int(input())
array = list(map(int, input().split()))
lis = [1] * n
for i in range(1, n):
for j in range(i):
if array[i] > array[j]:
lis[i] = max(lis[i], lis[j] + 1)
print(max(lis))
1. 다이나믹 프로그래밍
n = int(input())
array = list(map(int, input().split()))
array.reverse() #순서 뒤집어서 '가장 긴 증가하는 부분 수열'로 변환
dp = [1] * n
for i in range(1, n):
for j in range(0, i):
if array[j] < array[i]:
dp[i] = max(dp[i], dp[j] + 1)
#최소수를 출력
print(n - max(dp))
-
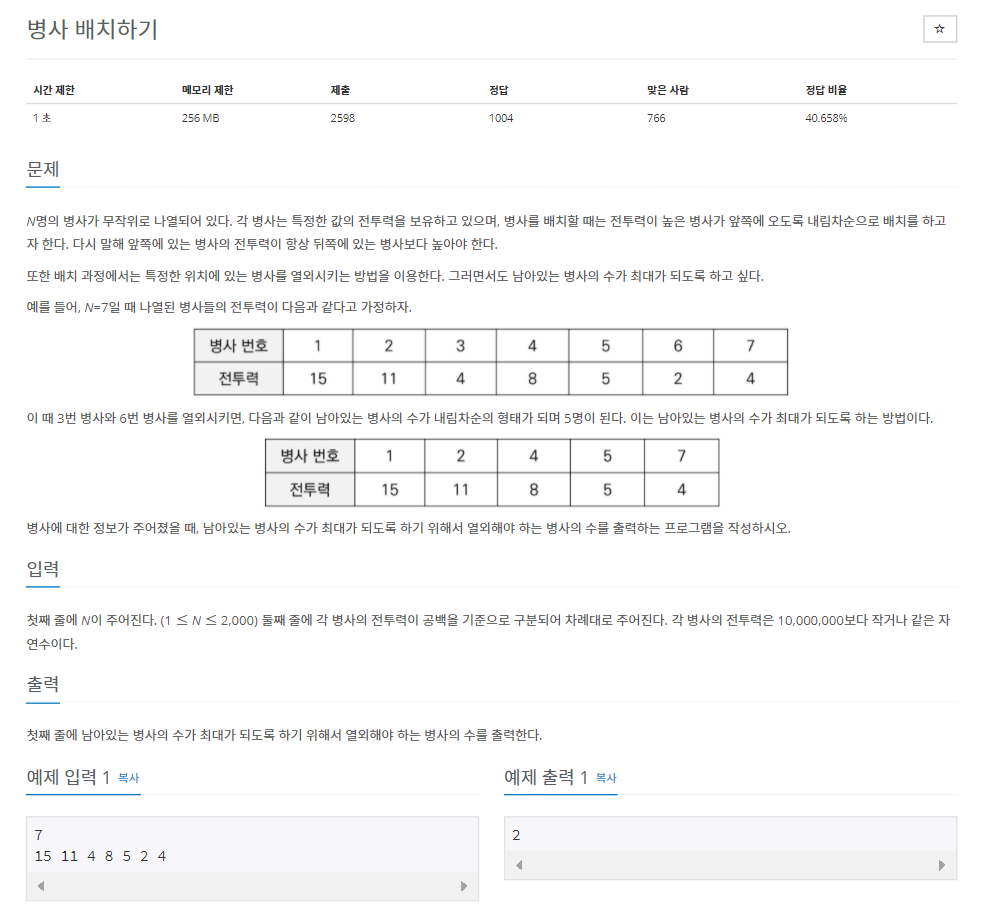
병사를 배치할 때 전투력이 높은 병사가 앞쪽에 오도록 내림차순 배치
- 이는 '가장 긴 감소하는 부분 수열'의 길이를 계산하는 문제로 간주할 수 있다.
2. C++
#include <bits/stdc++.h>
using namespace std;
int n;
vector<int> v;
int main(void) {
cin >> n;
for (int i = 0; i < n; i++) {
int x;
cin >> x;
v.push_back(x);
}
// 순서를 뒤집어 '최장 증가 부분 수열' 문제로 변환
reverse(v.begin(), v.end());
// 다이나믹 프로그래밍을 위한 1차원 DP 테이블 초기화
int dp[2000];
for (int i = 0; i < n; i++) {
dp[i] = 1;
}
// 가장 긴 증가하는 부분 수열(LIS) 알고리즘 수행
for (int i = 1; i < n; i++) {
for (int j = 0; j < i; j++) {
if (v[j] < v[i]) {
dp[i] = max(dp[i], dp[j] + 1);
}
}
}
// 열외해야 하는 병사의 최소 수를 출력
int maxValue = 0;
for (int i = 0; i < n; i++) {
maxValue = max(maxValue, dp[i]);
}
cout << n - maxValue << '\n';
}
