94. 1이 될 때 까지

• 어떠한 수 N이 1이 될 때까지 다음의 두 과정 중 하나를 반복적으로 선택하여 수행하려고 한다.

  • 단, 두번째 연산은 N이 K로 나누어떨어질 때만 선택할 수 있다.

    1. N에서 1을 뺀다.

    2. N에서 K로 나눈다.

N이 17, K가 4라고 가정하자.
이 때 1번의 과정을 한 번 수행하면 N은 16이 된다. 이후에 2번의 과정을 두 번 수행하면 N은 1이 된다. 결과적으로 이 경우 전체 과정을 실행한 횟수는 3이 된다.

• 입력조건

  • 첫째 줄에 N(2 ≤ N ≤ 100,000)과 K(2 ≤ K ≤ 100,000)가 공백으로 구분되며 각각 자연수로 주어진다.

    • 이때 입력으로 주어지는 N은 항상 K보다 크거나 같다.

• 출력조건

  • 첫째 줄에 N이 1이 될 때까지 1번 혹은 2번의 과정을 수행해야 하는 횟수의 최솟값을 출력한다.

1. 반복문을 이용한 경우

n,k = map(int, input().split())
result = 0

#N이 K 이상이라면 K로 계속 나누기
while n >= k:
  #N이  K로 나누어 떨어지지 않는다면 N에서 1씩 빼기
  while n % k != 0:
    n -= 1
    result += 1
  #K로 나누기
  n //=k
  result += 1

#마지막으로 남은 수에 대하여 1씩 빼기
while n > 1:
  n -= 1
  result += 1

print(result)

• 주어진 N에 대하여 '최대한 많이 나누기'를 수행하면 된다.

  • 문제에서는 K가 2 이상의 자연수이므로, 가능하면 나누는 것이 항상 더 숫자를 빠르게 줄이는 방법이 된다.

• N이 클수록 K로 나누었을 때 줄어드는 양이 더 많다.

  • N이 처음엔 큰 수라고 해도 나누기를 수행하면서 크기가 빠르게 줄어든다.

  • K가 2 이상이기만 하면 K로 나누는 것이 1을 빼는 것보다 항상 빠르게 N의 값을 줄일 수 있으며, N이 결국 1에 도달한다는 것을 알 수 있다.

  • 그러므로 K로 최대한 많이 나눌 수 있도록 하는 것이 최적의 해를 보장하는 것이다.

2. 최적화

import time




n,k = map(int, input().split())

result = 0


start = time.time()

#N이 K 이상이라면 K로 계속 나누기
while True:
  #(N == K로 나누어떨어지는 수)가 될 때까지 1씩 빼기
  target = (n // k) * k
  result += (n - target)
  n = target

  #N이 K보다 작을 때 (더 이상 나눌 수 없을 때) 반복문 탈출
  if n < k:
    break

  #K로 나누기
  result += 1
  n //= k

#마지막으로 남은 수에 대하여 1씩 빼기
result += (n - 1)

print(result)

print(time.time()-start)

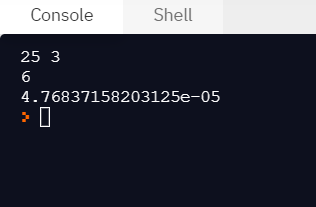
• N이 100억 이상의 큰 수가 되는 경우를 가정했을 때에도 빠르게 동작하려면, N이 K의 배수가 되도록 효율적으로 한 번에 빼는 방식으로 소스코드를 작성할 수 있다.