208. 정확한 순위

• 선생님은 시험을 본 학생 N명의 성적을 분실하고, 성적을 비교한 결과의 일부만 가지고 있습니다.

• 학생들의 성적을 빅한 결과가 주어질 때, 성적 순위를 정확히 알 수 있는 학생은 모두 몇 명인지 계산하는 프로그램을 작성하시오.

• 입력조건

  • 첫째 줄에 학생들의 수 N (2≤N≤500)과 두 학생의 성적을 비교한 횟수 M(2≤M≤10,000)이 주어집니다.

  • 다음 M개의 각 줄에는 두 학생의 성적을 비교한 결과를 나타내는 두 양의 정수 A와 B가 주어집니다.

    • 이는 A번 학생의 성적이 B번 학생보다 낮다는 것을 의미합니다.

• 출력조건

  • 첫째 줄에 성적 순위를 정확히 알 수 있는 학생이 몇 명인지 출력합니다.

1. 플로이드 워셜

INF = int(1e9)
n, m = map(int, input().split())

graph = [[INF] *(n + 1) for _ in range(n + 1)]

for a in range(n + 1):
  for b in range(n + 1):
    if a == b:
      graph[a][b] = 0

for _ in range(m):
  a, b = map(int, input().split())
  graph[a][b] = 1

for k in range(1, n + 1):
  for i in range(1, n + 1):
    for j in range(1, n + 1):
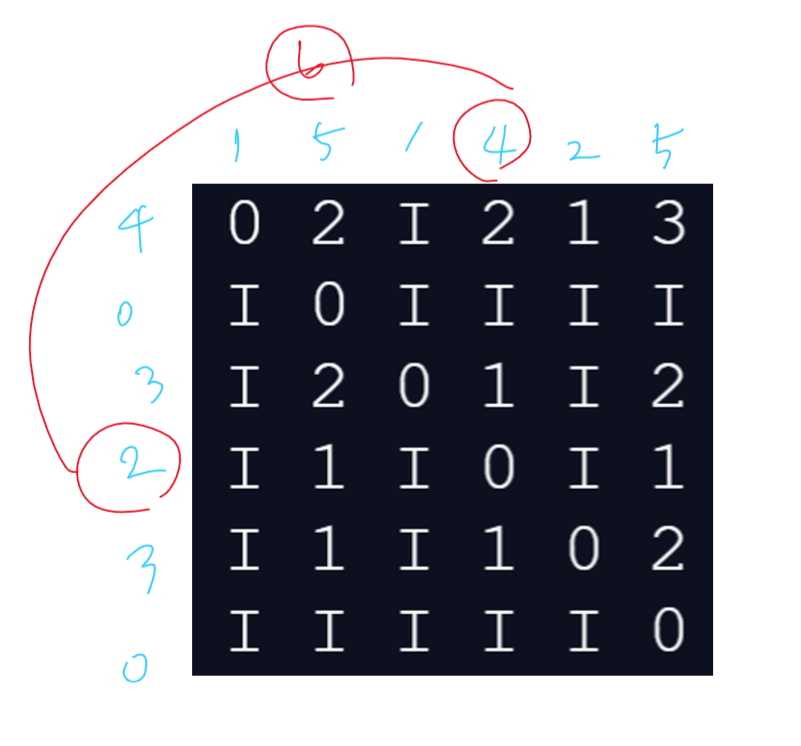
      graph[i][j] = min(graph[i][j], graph[i][k] + graph[k][j])

result = 0

#각 학생 번호에 따라 한 명씩 확인하며 도달 가능한지 체크
for i in range(1, n + 1):
  count = 0
  for j in range(1, n + 1):
    if graph[i][j] != INF or graph[j][i] != INF:
      count += 1
  if count == n:
    result += 1

print(result)

2. C++

#include <bits/stdc++.h>
#define INF 1e9 // 무한을 의미하는 값으로 10억을 설정

using namespace std;

// 노드의 개수(N), 간선의 개수(M)
int n, m;
// 2차원 배열(그래프 표현)를 만들기
int graph[501][501];

int main(void) {
    cin >> n >> m;

    // 최단 거리 테이블을 모두 무한으로 초기화
    for (int i = 0; i < 501; i++) {
        fill(graph[i], graph[i] + 501, INF);
    }

    // 자기 자신에서 자기 자신으로 가는 비용은 0으로 초기화
    for (int a = 1; a <= n; a++) {
        for (int b = 1; b <= n; b++) {
            if (a == b) graph[a][b] = 0;
        }
    }

    // 각 간선에 대한 정보를 입력 받아, 그 값으로 초기화
    for (int i = 0; i < m; i++) {
        // A에서 B로 가는 비용은 C라고 설정
        int a, b;
        cin >> a >> b;
        graph[a][b] = 1;
    }
    
    // 점화식에 따라 플로이드 워셜 알고리즘을 수행
    for (int k = 1; k <= n; k++) {
        for (int a = 1; a <= n; a++) {
            for (int b = 1; b <= n; b++) {
                graph[a][b] = min(graph[a][b], graph[a][k] + graph[k][b]);
            }
        }
    }

    int result = 0;
    // 각 학생을 번호에 따라 한 명씩 확인하며 도달 가능한지 체크
    for (int i = 1; i <= n; i++) {
        int cnt = 0;
        for (int j = 1; j <= n; j++) {
            if (graph[i][j] != INF || graph[j][i] != INF) {
                cnt += 1;
            }
        }
        if (cnt == n) {
            result += 1;
        }
    }
    cout << result << '\n';
}