273. MinMaxDivision

• 이분화할 대상을 찾아야 합니다. 이 질문은 결과를 둘로 나누어야 합니다.

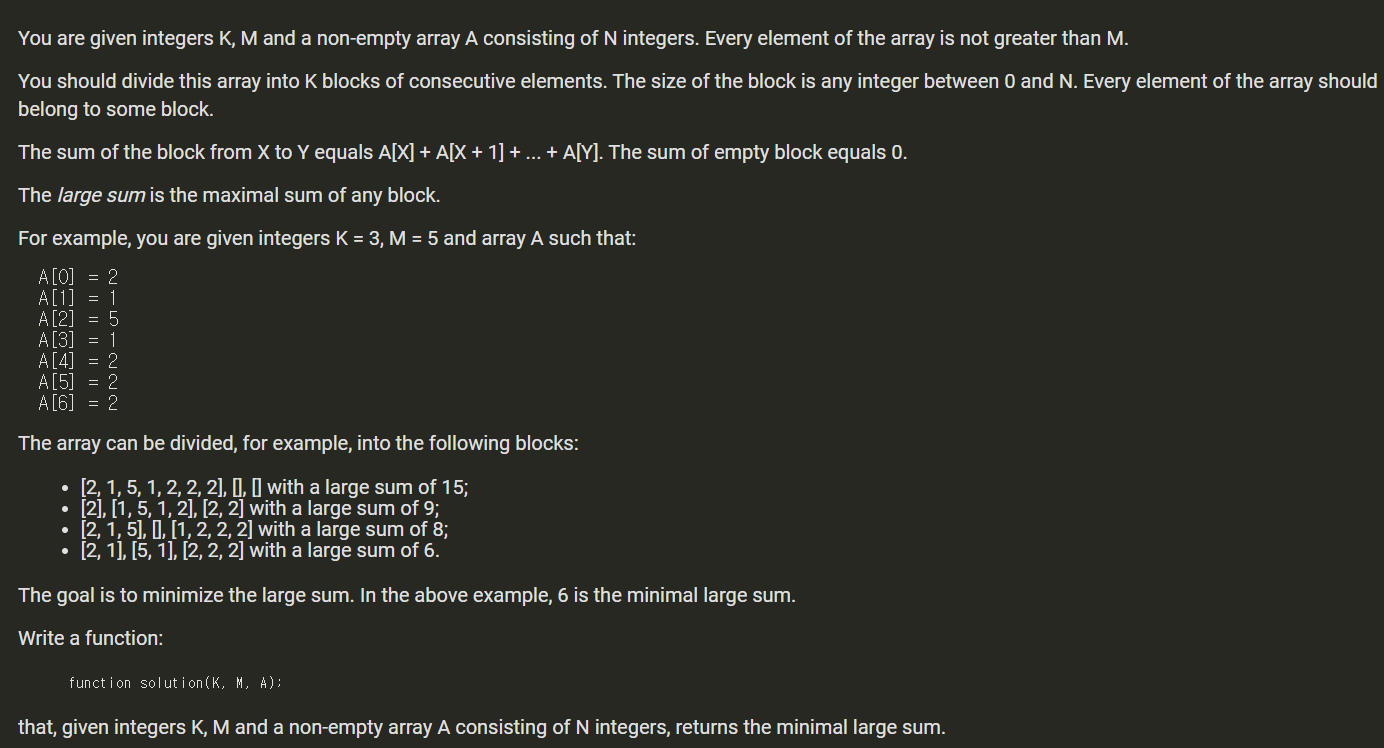
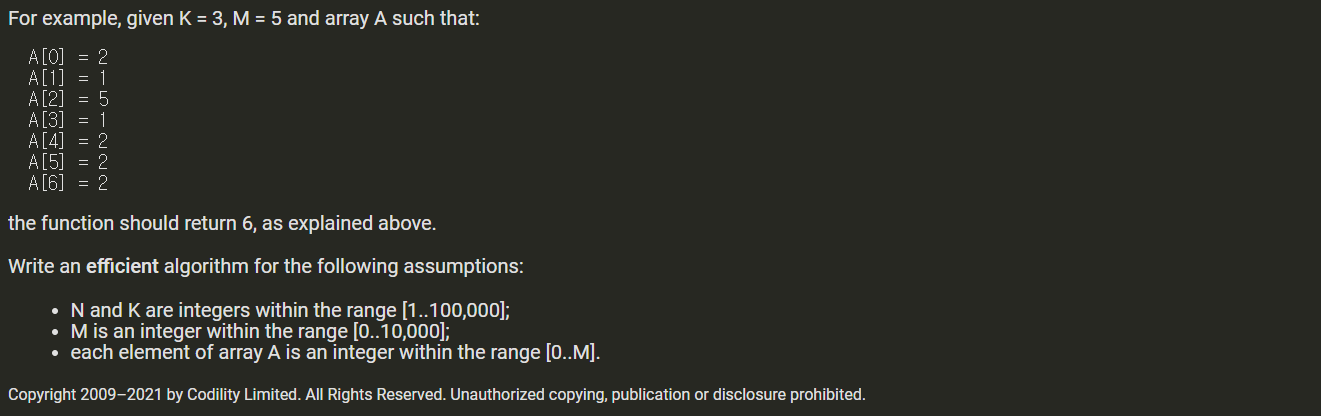
  • k 블록에서 가장 큰 배열 합계의 최소값입니다.

• 0에서 합으로 나눈 다음 이분법의 판단 조건

  • 배열을 k개 이하의 블록으로 나눌 수 있는지

  • 각 블록의 합이 중간 이하인지 여부입니다.

• 조건을 만족한다면 mid의 값이 너무 크다는 의미이며 더 작아질 수 있습니다.

1. JavaScript

function solution(K, M, A) {
    let begin = A.reduce((a, v) => (a + v), 0);
    begin = parseInt((begin+K-1)/K);
    let max = Math.max(A);
    if (max > begin) begin = max;

    let end = begin + M + 1;
    let res = 0;

    while(begin <= end) {
        let mid = (begin + end) / 2;
        let sum = 0;
        let block = 1;
        for (let ind in A) {
            let a = A[ind];
            sum += a;
            if (sum > mid) {
                ++block;
                if (block > K) break;
                sum = a;
            }
        }
        if (block > K) {
            begin = mid + 1;
        } else {
            res = mid;
            end = mid - 1;
        }
    }
    return res;
}

2. Python

# you can write to stdout for debugging purposes, e.g.
# print("this is a debug message")

def isValid(A, cnt, size):
    b_sum = 0
    b_cnt = 0

    #블럭 최대값 넘으면 블럭 나누기
    for i in A:
        if b_sum + i > size:
            b_sum = i
            b_cnt += 1

        else:
            b_sum += i
        
        if b_cnt >= cnt:
            return False
    return True
    
def solution(K, M, A):
    # write your code in Python 3.6
    cnt = K
    left = max(A)
    right = sum(A)

    if cnt == 1:
        return right
    if cnt >= len(A):
        return left
    
    while(left <= right):
        mid = (left + right) // 2
        if isValid(A, cnt, mid):
            right = mid - 1
        else:
            left = mid + 1

    return left