61. Largest Number

리트코드

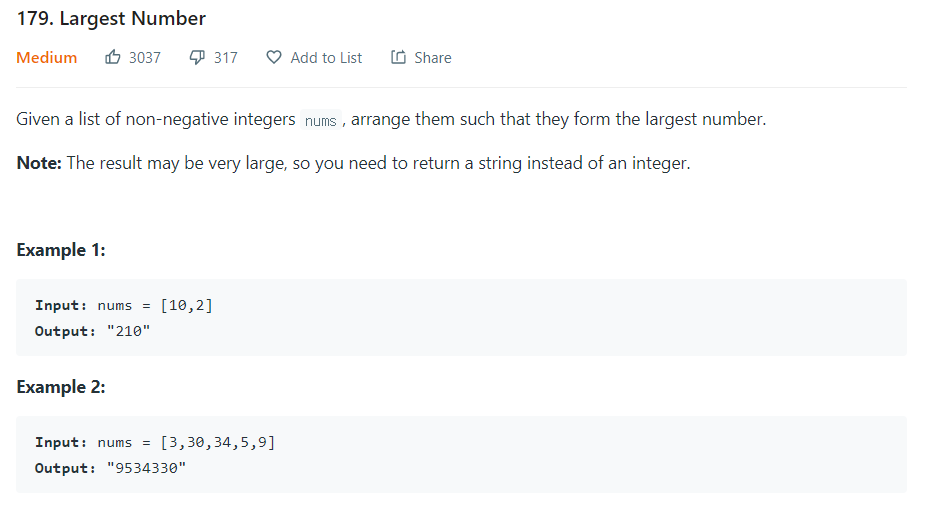
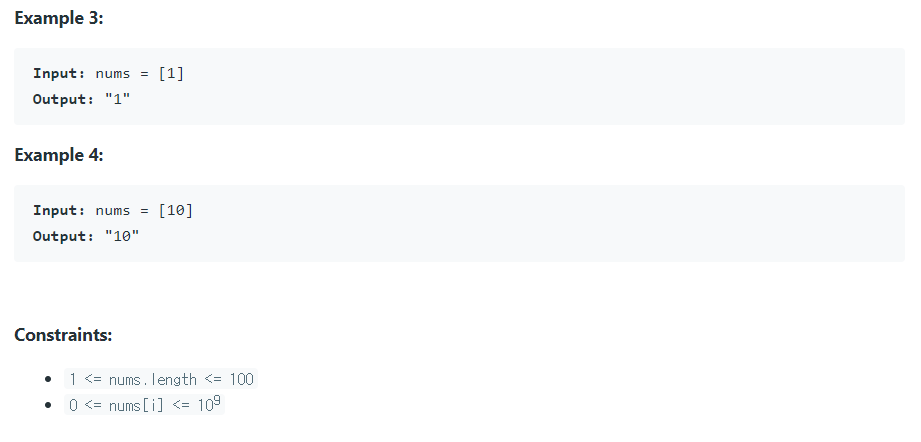
• 항목들을 조합하여 만들 수 있는 가장 큰 수를 출력하라.

1. 삽입 정렬

class Solution:
    
    #문제에 적합한 비교 함수
    @staticmethod
    def to_swap(n1: int, n2: int) -> bool:
        return str(n1) + str(n2) < str(n2) + str(n2)
     
    #삽입 정렬 구현  
    def largestNumber(self, nums: List[int]) -> str:
        i = 1
        while i < len(nums):
            j = i
            while j > 0 and self.to_swap(nums[j - 1], nums[j]):
                nums[j], nums[j - 1] = nums[j - 1], nums[j]
                j -= 1
            i += 1
            
        return str(int(''.join(map(str, nums))))
       
       

• 각 요소 단위로 크기 순으로 정렬하면 된다.

  • 단 여기서는 다소 특이한 정렬 기법을 적용해야 하는데 맨 앞에서부터 자릿수 단위로 비교해서 크기 순으로 정렬한다.

  • 9는 30보다 맨 앞자리수가 더 크므로 9가 더 앞에 와야한다.

    • 930이 큰지 309가 큰지 비교하는 문제로 풀 수 있을 것 같다.

• a + b와 b + a를 비교하는 형태로 처리할 수 있다.

  • to_swap()함수의 결과가 True라면 위치 변경이 이뤄져야 한다.

• 앞서 문제의 풀이는 연결 리스트에 대한 풀이이며, 이문제는 배열이기 때문에 인덱스를 지정할 수 있어서 전반적으로 코드가 많이 달라진다.

<삽입 정렬 수도코드>

i <- 1
while i < length(A)
    j <- i
    while j > 0 and A[j-1] > A[j]
    	swap A[j] and A[j-1]
        j <- j - 1
    end while
    i <- i + 1
end while

• 파이썬 코드가 수도코드 알고리즘과 다른 한 가지 부분이라면, 수도코드의 while문의 A[j-1] > A[j] 비교를 self.to_swap(nums[j - 1], nums[j]) 비교로 변경한 부분이다.

  • 이 부분은 이전 값이 더 커서 스왑이 필요한지 여부를 체크하는 로직인데,

    우리는 이 부분을 문제에 적합하게 단순 비교가 아닌 to_swap()이라는 함수를 통해 스왑 여부를 판별할 수 있도록 구현했고,

    따라서 이 함수를 호출하는 형태로 코드를 변경했다.

• 배열은 이처럼 깔끔하게 구현할 수 있기 때문에 연결 리스트 때처럼 포인터를 맨 앞으로 돌릴지 비교하는 등의 최적화는 수행할 필요가 없다.

  • 아울러 정렬된 리스트 변수를 별도로 선언했던 것과 달리 원래 삽입 정렬을 배열로 구현하게 되면, 이처럼 제자리 정렬(In-Place Sort)이 가능하여 공간 복잡도도 줄일 수 있다.

• 마지막에 리턴하는 부분이 다소 번잡하다.

  • 원래 ''.join(map(str, nums)) 정도면 끝나게 되겠지만,
    여기서는 입력값이 ["0", "0"]인 경우도 있기 때문에 그냥 문자로 처리해버리면 리턴값이 00이 되기 때문이다.

  • 따라서 join()결과를 int로 바꿔서 00이 0이 되도록 만들어 준 후, 다시 str으로 변경해서 그런 일이 없게 했다.