-
두 정수
a와b의 합을 구하라.+또는-연산자는 사용할 수 없다.
1. 전가산기 구현 (28ms)
class Solution:
def getSum(self, a: int, b: int) -> int:
MASK = 0xFFFFFFFF
INT_MAX = 0x7FFFFFFF
a_bin = bin(a & MASK)[2:].zfill(32)
b_bin = bin(b & MASK)[2:].zfill(32)
result = []
carry = 0
sum = 0
for i in range(32):
A = int(a_bin[31 - i])
B = int(b_bin[31 - i])
#전가산기 구현
Q1 = A & B
Q2 = A ^ B
Q3 = Q2 & carry
sum = carry ^ Q2
carry = Q1 | Q3
result.append(str(sum))
if carry == 1:
result.append('1')
#초과 자리수 처리
result = int(''.join(result[::-1]), 2) & MASK
#음수 처리
if result > INT_MAX:
result = ~(result ^ MASK)
return result
-
이번에는 좀 더 제대로 전가산기를 구현해본다. 물론 전가산기를 온전히 구현하는 데는 많은 노력이 필요하다.
- 지나치게 어렵게 풀이하는 것 같지만, 여기서는 논리 회로에 대한 이해도 높일 겸 한 번 제대로 구현을 시도해본다.
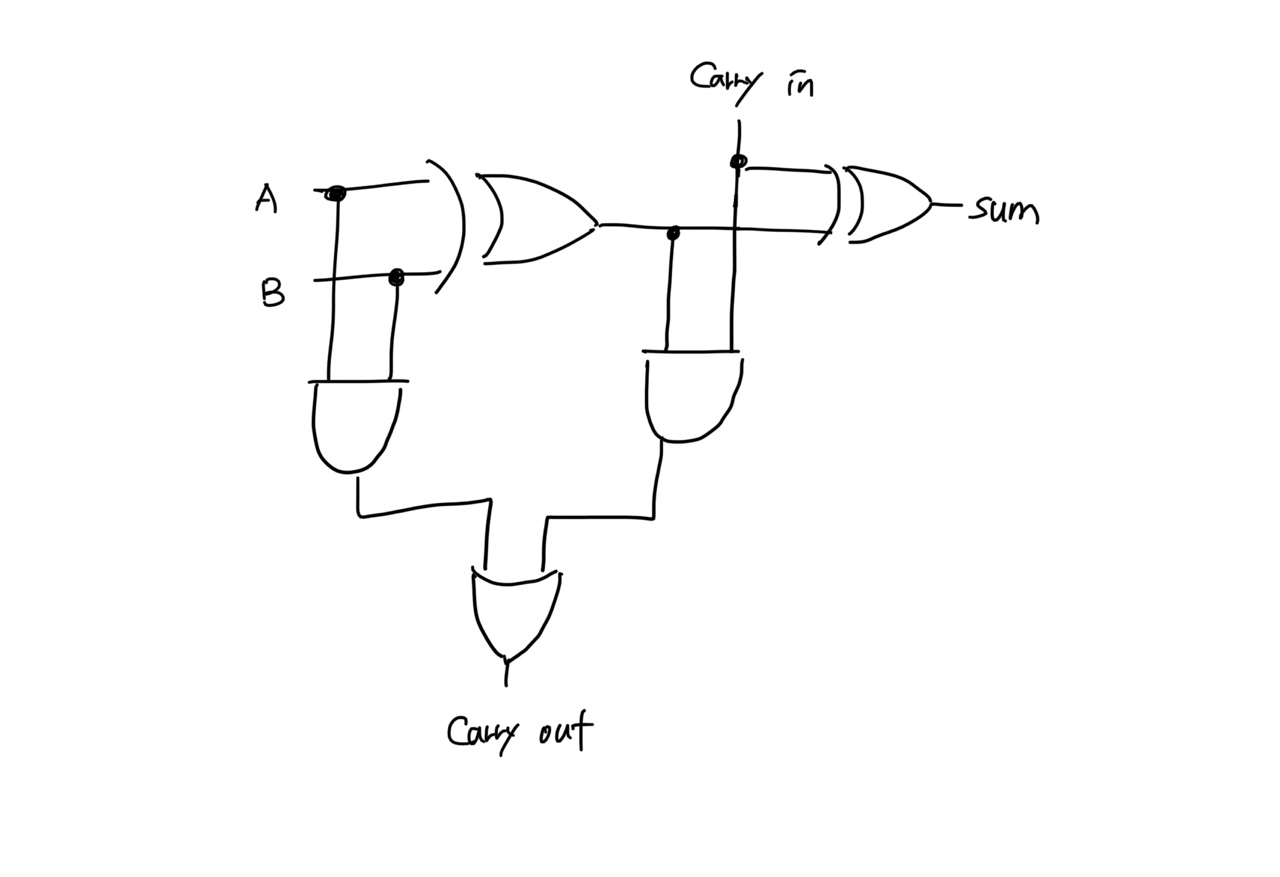
<전가산기 회로도>
- 전가산기 회로도는 AND 게이트 2개, XOR 게이트 2개, OR 게이트 1개로 이루어져 있다.
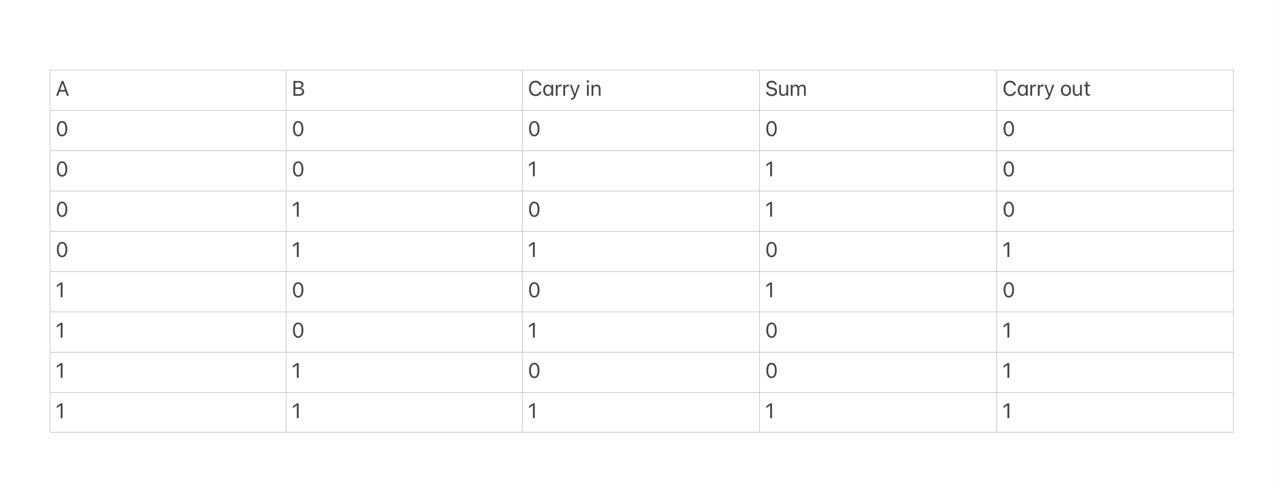
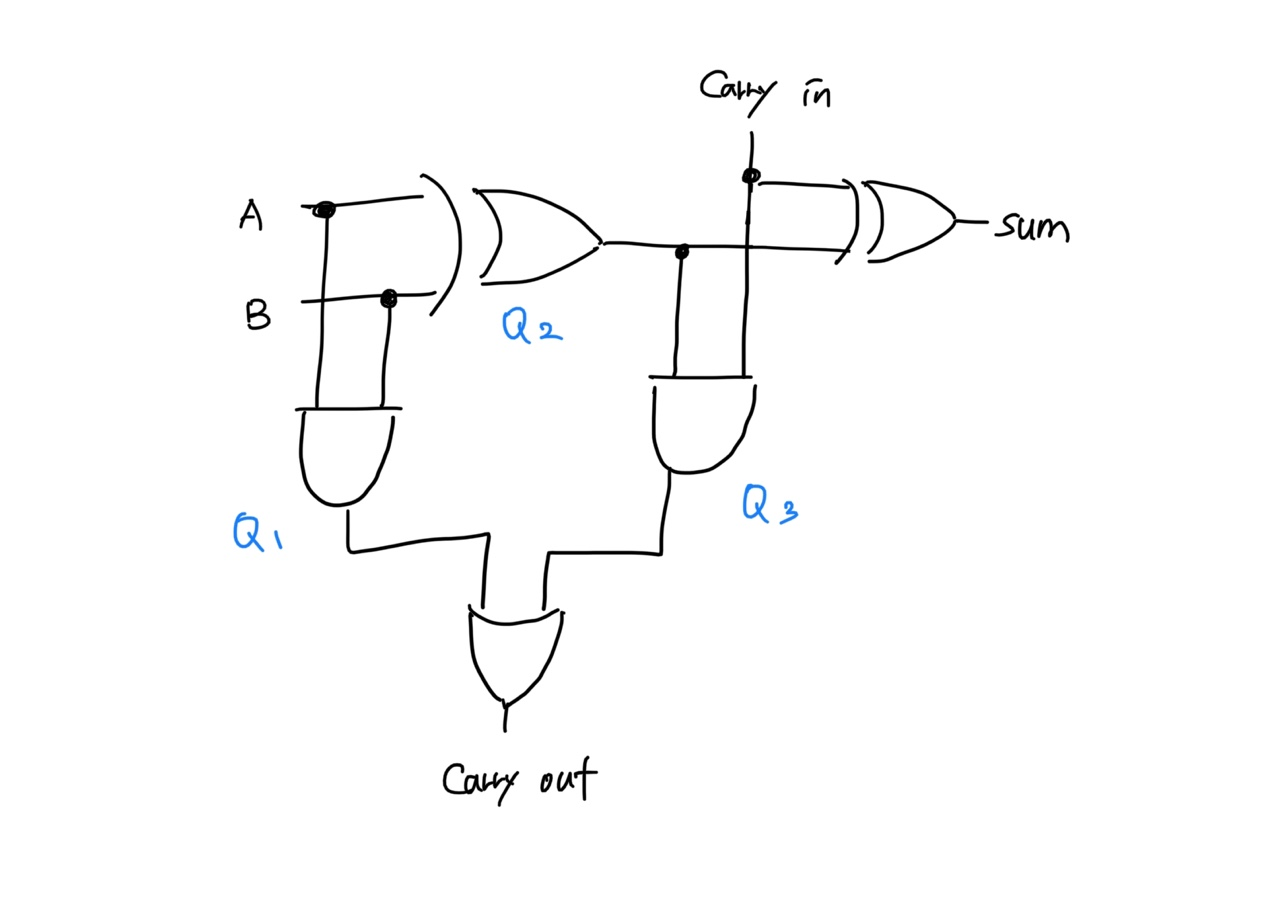
<각각의 게이트 위치 중간값 표현>
-
그림의 중간값 변수
Q1,Q2,Q3에 회로도의 연산을 통해 직접 계산해보자.-
이를 파이썬 코드로 구현하면 다음과 같다.
Q1 = A & B Q2 = A ^ B Q3 = Q2 & carry sum = carry ^ Q2 carry = Q1 | Q3 -
각각의 비트는 이렇게 전가산기를 통해 합
sum을 구하는 로직으로 처리할 수 있게 되었다.
-
-
다음으로 이를 위한 전처리를 진행한다.
-
bin()이라는 함수는 십진수10을0b1010으로 변환해준다. -
이 때 앞에
0b식별자가 항상 붙는다.- 우리에게는 필요 없는 값이므로, 슬라이싱
bin(a)[2:0]로 이 부분을 떼낸다.
- 우리에게는 필요 없는 값이므로, 슬라이싱
-
MASK는 비트 마스크로, 음수 처리를 위해 2의 보수로 만들어주는 역할을 한다.-
여기서는 입력값을 32비트 정수로 가정했으므로
MASK는0xFFFFFFFF로 했고, 이 값을 AND 연산하면 이제 결과는 2의 보수 값을 취하게 된다.bin(1 & MASK) -> 0b1'
bin(-1 & MASK) -> 0b111111111111111111111111111111'
-
-
양수인 경우 마스킹을 해도 동일하지만 음수인
-1은 2의 보수에서 가장 큰 값이기 때문에, 이처럼 마스킹을 할 경우 32비트 전체가 1로 꽉 채워지는 모습을 확인할 수 있다.-
z.fill(32)로 32비트 자릿수를 맞춰준다. -
앞자리가 비어 있으면 계산을 어렵게하기 때문이다.
-
-
-
전처리를 다 끝내었고 이제 처리한 값을 뒷부분부터, 즉 낮은 자릿수부터 하나씩 전가산기를 통과하면서 결과를 채워나가면 된다.
- 여기서는 32비트를 가정했으므로 32번 반복한다.
-
마지막 반복이 끝난 후 아직
carry값이 남아 있다면 자릿수가 하나 더 올라간 것이므로,1을 더 추가한다.- 이렇게 되면 최대 33비트가 되겠지만, 마지막 마스킹 작업을 통해 이 값은 날아가게 될 것 이다.
-
result는 낮은 자릿수부터 채웠으므로, 뒤집은 다음 십진수 정수로 바꿔준다.- 다음으로 마스킹을 해서, 만약 자릿수를 초과했다면 그 값은 제거될 수 있게 한다.
-
마지막으로 음수를 처리하는데, 2의 보수에서 음수는 32번째 비트의 값, 즉 최상위 비트(MSB)가 1인 경우다.
- 양의 정수 최댓값은
0x7FFFFFFF이므로, 만약 32번째 비트가 1이라면 이보다 큰 값이 되고, 이 경우 마스킹 값과 XOR한 다음 NOT 처리를 해서 다시 음수로 만들어준다.
- 양의 정수 최댓값은
2. 좀 더 간소한 구현 (24ms)
class Solution:
def getSum(self, a: int, b: int) -> int:
MASK = 0xFFFFFFFF
INT_MAX = 0x7FFFFFFF #양수의 최댓값
a_bin = bin(a & MASK)[2:].zfill(32)
b_bin = bin(b & MASK)[2:].zfill(32)
#합, 자릿수 처리
while b != 0:
a,b = (a ^ b) & MASK, ((a & b) << 1) & MASK
#음수 처리
if a > INT_MAX:
a = ~(a ^ MASK)
return a
-
여기서는 핵심만 살려서 간단하게 동작 가능하게 한다.
-
MASK는 2의 보수로 만들기 위한 것으로, 이전 풀이와 동일한 값이다. -
a와b의 역할을 구분해a에는carry값을 고려하지 않는a와b의 합(sum)이 담기게 하고,b에는 자릿수를 올려가며carry값이 담기게 했다. -
다음으로 음수에 대한 처리를 해준다.
- XOR -> NOT
