75. Sliding Window Maximum

리트코드

• 배열 nums가 주어졌을 때 k 크기의 슬라이딩 윈도우를 오른쪽 끝까지 이동하면서 최대 슬라이딩 윈도우를 구하라.

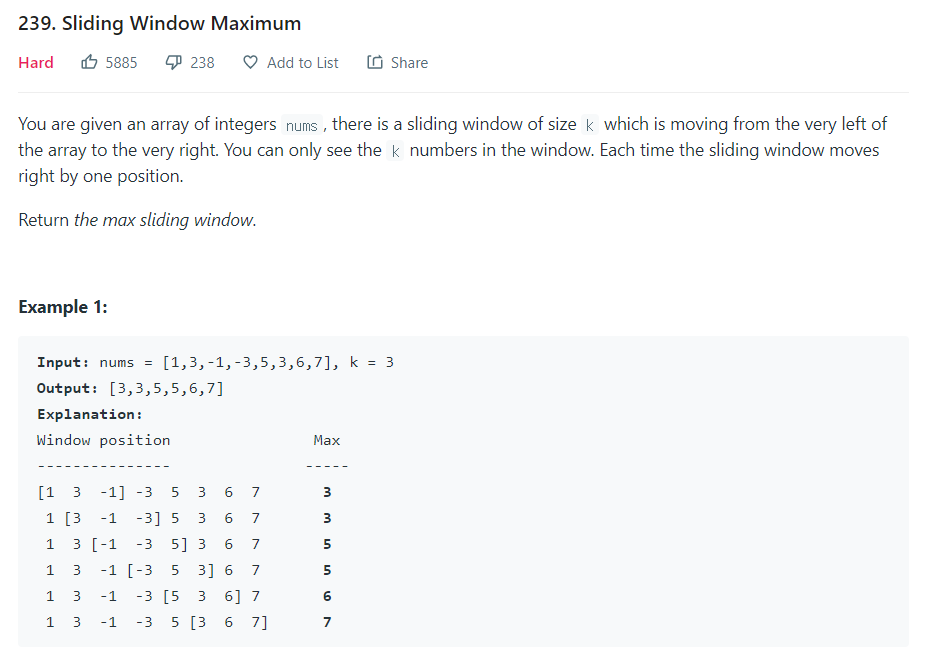
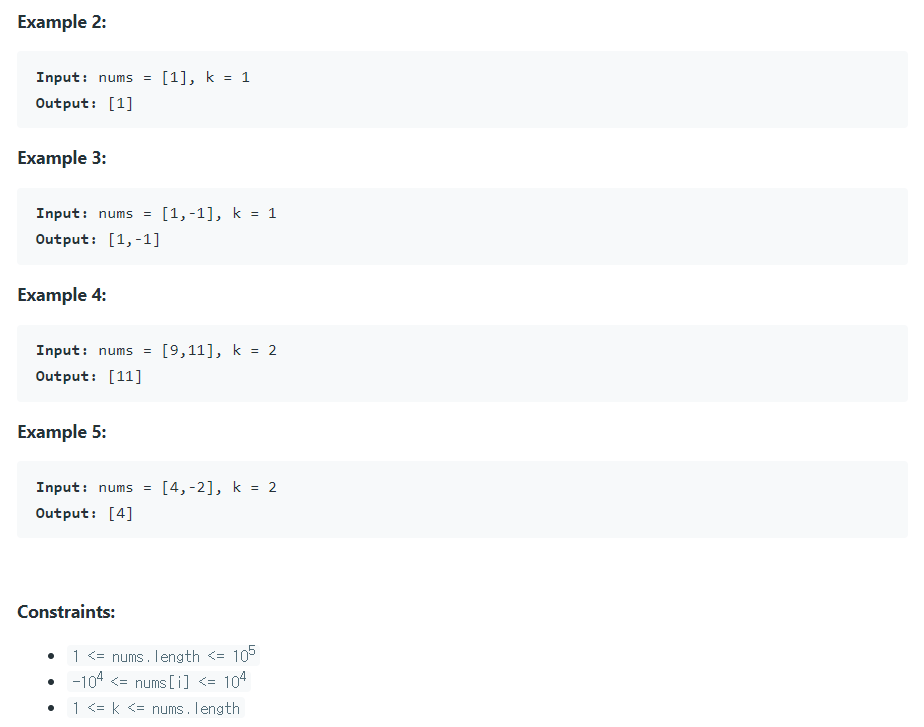
1. 브루트 포스로 계산 (704ms)

class Solution:
    def maxSlidingWindow(self, nums: List[int], k: int) -> List[int]:
        
        if not nums:
            return nums
        
        r = []
        for i in range(len(nums) - k + 1):
            r.append(max(nums[i:i + k]))
            
        return r

• 제목부터 '슬라이딩 윈도우'라는 단어가 포함된 전형적인 슬라이딩 윈도우 문제로, 파이썬에서는 슬라이싱과 내장 함수를 사용해 매우 쉬운 방식으로 풀이할 수 있을 것 같다.

• 이 코드는 정확히 문제에서 요구하는 대로, 슬라이딩 윈도우를 우측으로 움직여 가며 max()로 최댓값을 추출한다.

  • 매번 윈도우의 최댓값을 계산하기 때문에 이 경우 시간 복잡도는 O(n) 이다.

2. 큐를 이용한 최적화 (156ms)

class Solution:
    def maxSlidingWindow(self, nums: List[int], k: int) -> List[int]:
        
        results = []
        window = collections.deque()
        current_max = float('-inf');
        for i, v in enumerate(nums):
            window.append(v)
            if i< k - 1:
                continue
                
            #새로 추가된 값이 기존 최댓값보다 큰 경우 교체
            if current_max == float('-inf'):
                current_max = max(window)
            elif v > current_max:
                current_max = v

            results.append(current_max)

            #최댓값이 윈도우에서 빠지면 초기화
            if current_max == window.popleft():
                current_max = float('-inf')
    
        return results

• 어차피 슬라이딩 윈도우를 한 칸씩 움직여야하는 부분은 개선이 어렵다.

• 그렇다면 max()를 계산하는 부분에서 최적화를 할 수 있지 않을까?

  • 정렬되지 않은 슬라이딩 윈도우에서 최댓값을 추출하려면 어떠한 알고리즘이든 결국 한 번 이상은 봐야 하기 때문에, 최댓값 계산을 O(n) 이내로 줄일 수 있는 방법이 없다.

  • 최댓값 계산을 최소화하기 위해 이전의 최댓값을 저장해뒀다가 한 칸씩 이동할 때 새 값에 대해서만 더 큰 값인지 확인하고, 최댓값이 윈도우에서 빠지게 되는 경우에만 다시 전체를 계산하는 형태로 개선한다면 계산량을 획기적으로 줄일 수 있을 것 같다.

• 선입선출 형태로 풀이할 수 있기 때문에, 이에 해당하는 큐를 사용해본다.

  • 이 부분에서는 k만큼, 이후 비즈니스 로직은 상관하지 않고 일단 값을 계속 채워 넣는다.

  • 파이썬에서는 큐 사용이 필요한 경우, 실제로는 기능이 많고 좀 더 성능이 좋은 데크를 주로 사용한다.

• 아직 최댓값이 반영된 상태가 아니라면, 현재 윈도우 전체의 최댓값을 계산해야 한다. 이미 최댓값이 존재한다면 새로 추가된 값이 기존 최댓값보다 더 큰 경우에만 최댓값을 교체한다.

  • 이 부분이 성능 개선을 위한 핵심이다.

  • 매번 최댓값을 계산할 필요가 없기 때문이다.

• 이처럼 새로 추가된 값이 기존 최댓값보다 더 큰 경우에만, 최댓값을 교체한다.

  • 그리고 최댓값을 결과에 추가한다.

• 슬라이딩 윈도우는 오른쪽으로 점차 이동한다.

  이동하면서 시작하자마자 다시 신규 요소가 추가될 것이므로 가장 오래된 값은 마지막에 제거한다.

  • 만약 그 값이 현재 윈도우의 최댓값이라면, 기존의 최댓값은 더 이상 윈도우에 포함되지 않으므로 최댓값에 시스템이 지정할 수 있는 가장 낮은 값을 지정하여 초기화한다.

    • 이렇게 하면 이후에 다시 최댓값을 계산하게 할 수 있다.

타임아웃으로 인한 다른 풀이 탐색

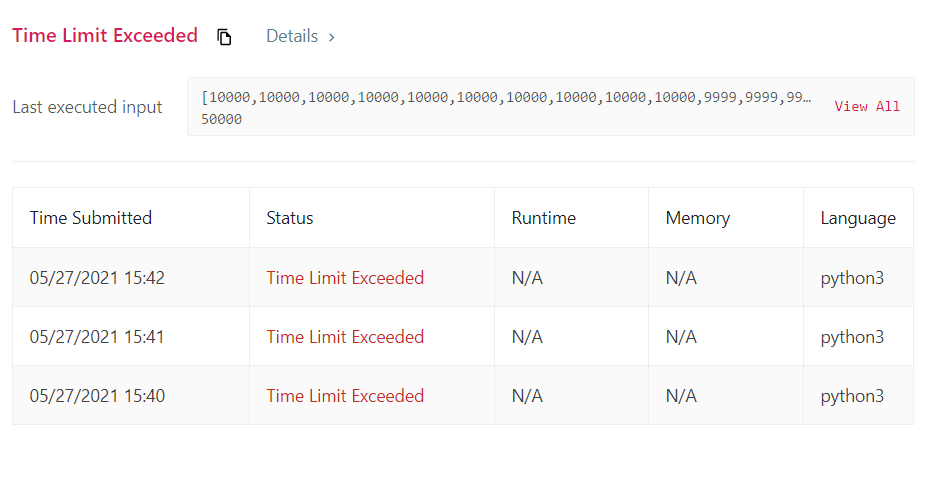
3. 데크를 이용한 풀이 (1700 ms)

(https://leetcode.com/problems/sliding-window-maximum/discuss/1202569/Python-solution-with-explanation-of-logic)

 def maxSlidingWindow(self, nums: List[int], k: int) -> List[int]:
        l = deque([])
        for i in range(k):
      		#이전 숫자가 현재 숫자보다 작다는 것을 발견하면 pop ②
            while l and nums[i]>=nums[l[-1]]:
                l.pop()
                
            #순서대로 deque에 넣어준다 ①
            l.append(i)
        #가장 큰 값은 우선순위 큐에서 첫번째 값
        ans = [nums[l[0]]]
		
        #window에서 첫 번째 숫자가 가장 크고 두 번째 숫자가 두 번째로 큰지 확인합니다
        for i in range(1,len(nums)-k+1):
            
            while(l and nums[i+k-1]>=nums[l[-1]]):
                l.pop()
                   
            l.append(i+k-1)
            
            #window가 지나면 가장 큰 것을 pop
            if i-1==l[0]:
                l.popleft()
            ans.append(nums[l[0]])
        return ans

• we can keep track of the largest number in the window by using deque

  • for example, if we have [1,2,3,4,3,2,1] in the window, we put each number into the deque sequentially

  • [] -> [1] ->[1,2], when we find the previous number is smaller than current number, we pop it from the deque

  • the logic behind it is that when we move the window from left to right, 2 is always in the window if 1 is in the window. so we don't need the information from 1.

  • this process ensures that the first number is the largest in the window, the second is second largest(if exits)

  • we have to do one more thing: pop the largest if the window passes