8. Trapping Rain Water

리트코드

1. 투포인터를 최대로 이동

class Solution:
    def trap(self, height: List[int]) -> int:
        if not height:
            return 0
        
        volume = 0
        
        left,right = 0, len(height) - 1
        left_max, right_max = height[left], height[right]
        
        while left < right:
        
            left_max, right_max = max(height[left], left_max), max(height[right], right_max)
            
            #더 높은 쪽을 향해 투 포인터 이동
            if left_max <= right_max:
                volume += left_max - height[left]
                left += 1
            
            else: 
                volume += right_max - height[right]
                right -= 1
        
        return volume
        

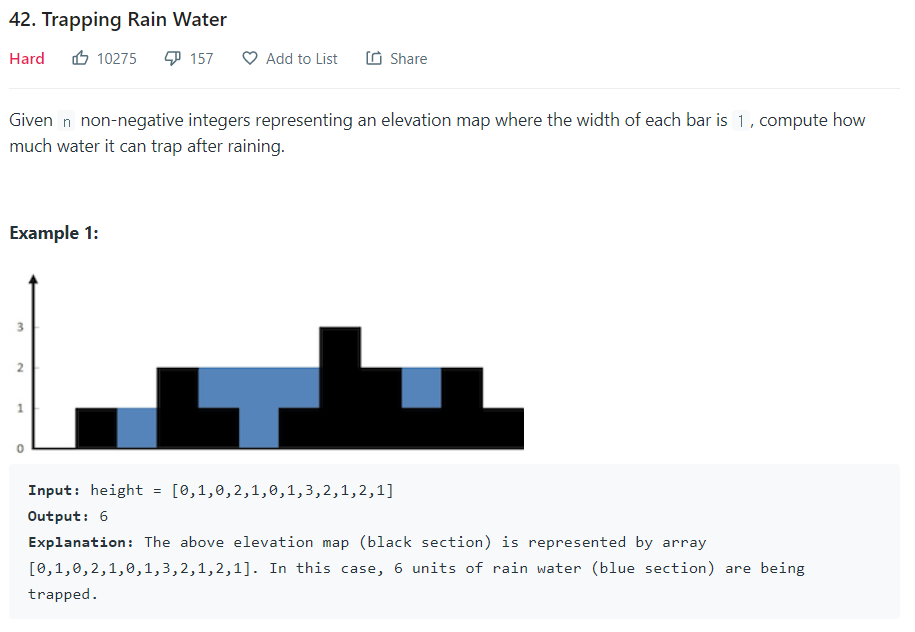
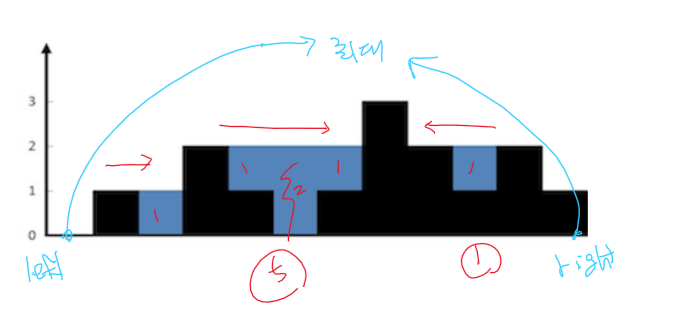
• 가장 높은 막대를 살펴보면 최대 높이는 3이지만 100이어도 상관이 없다.

• 막대는 높고 낮음에 무관하게, 전체 부피에 영향을 끼치지 않으면서 그저 왼쪽과 오른쪽을 가르는 장벽 역할을 한다.

• 최대 높이의 막대까지 각각 좌우 기둥 최대 높이 left_max, right_max가 현재 높이와의 차이만큼 물 높이 volume을 더해 나간다.

• 이 경우 적어도 낮은 쪽은 그만큼 항상 채워질 것이기 때문에, 좌우 어느 쪽이든 낮은 쪽은 높은 쪽을 향해서 포인터가 가우데로 점점 이동한다.

  • 오른쪽이 크다면 left += 1로 왼쪽이 이동
  • 왼쪽이 크다면 right -= 1로 오른쪽이 이동

• 최대지점에서 좌우 포인터가 서로 만나게 되며 O(n)에 풀이가 가능하다.

2. 스택 쌓기

class Solution:
    def trap(self, height: List[int]) -> int:
        stack = []
        volume = 0
        
        for i in range(len(height)):
            #변곡점을 만나는 경우
            while stack and height[i] > height[stack[-1]]:
                #스택에서 꺼낸다
                top = stack.pop()
                
                if not len(stack):
                    break
            
                #이전과의 차이만큼 물 높이 처리
                # stack[-1]은 제일 마지막에 들어온 애
                distance  = i - stack[-1] - 1
                waters = min(height[i], height[stack[-1]]) - height[top]
                
                volume += distance * waters
            stack.append(i)
            
        return volume

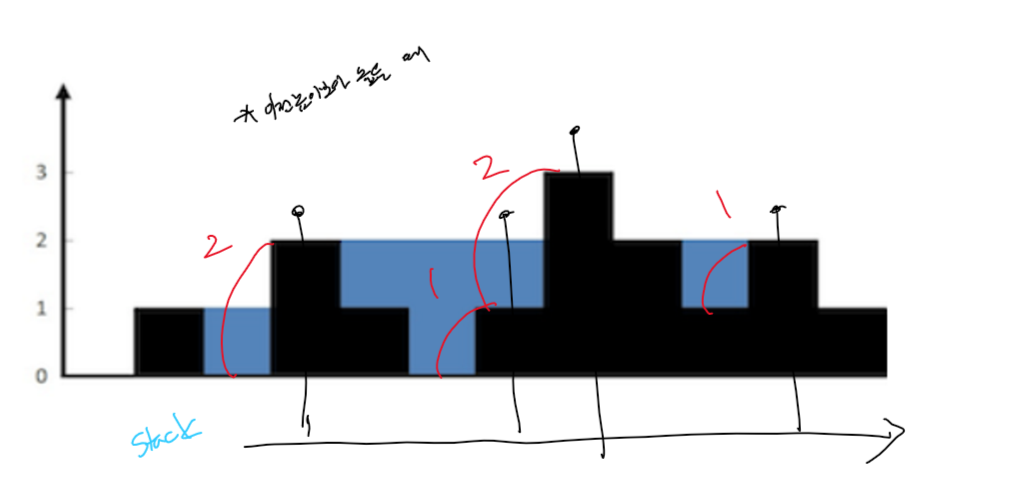
• 스택에 쌓아 나가면서 현재 높이가 이전 높이보다 높을 때, 즉 꺾이는 부분 변곡점(inflection point) 을 기준으로 격차만큼 물 높이 volume을 채운다.

• 이전 높이는 고정된 형태가 아니라 들쑥날쑥하기 때문에, 계속 스택으로 채워나가다가 변곡점을 만날 때마다 스택에서 하나씩 꺼내면서 이전과의 차이만큼 물 높이를 채워 나간다.

• 스택으로 이전 항목들을 되돌아보며 체크하기는 하지만, 기본적으로 한 번만 살펴보기 때문에 마찬가지로 O(n) 에 풀이가 가능하다.