-
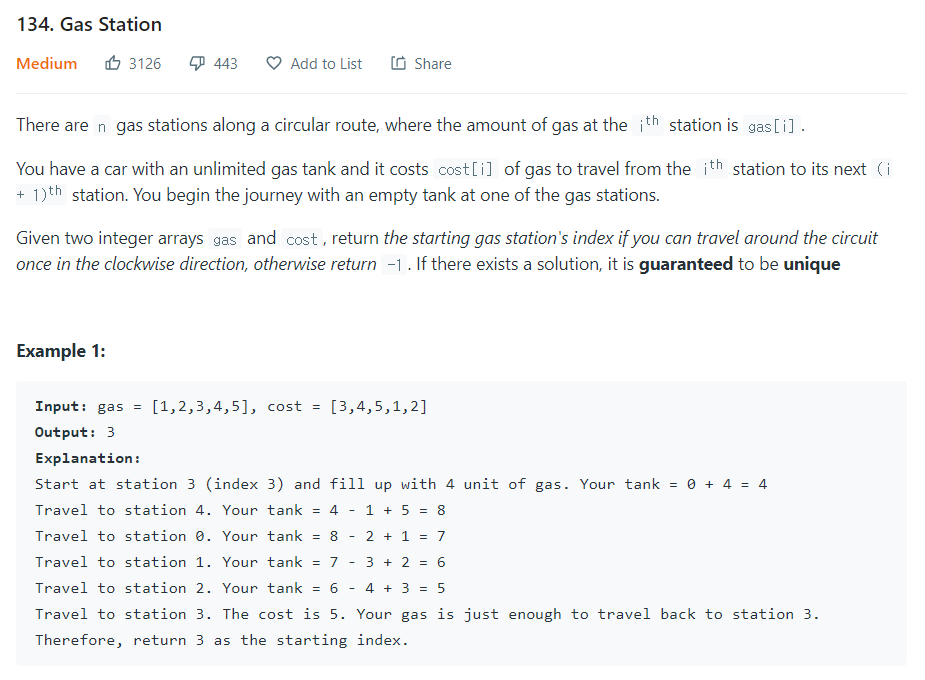
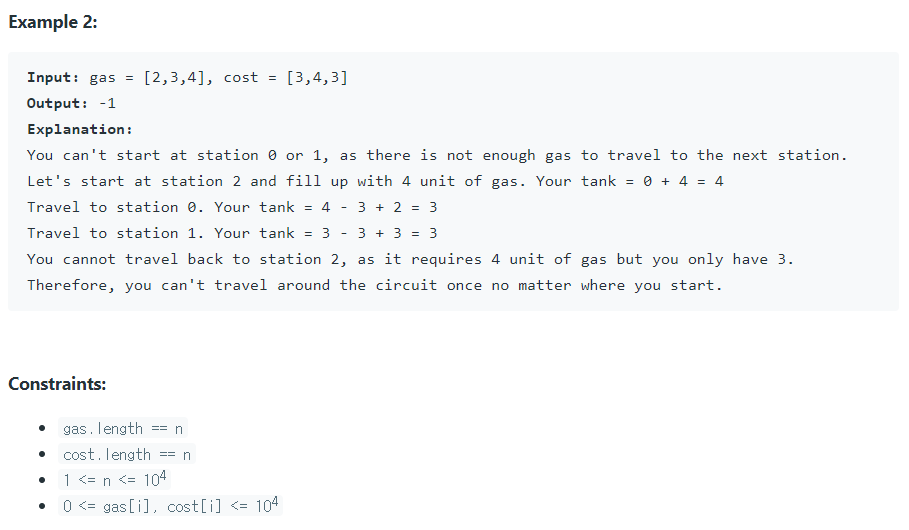
원형으로 경로가 연결된 주유소 목록이 있다.
각 주유소는gas[i]만큼의 기름을 갖고 있으며, 다음 주유소로 이동하는데cost[i]가 필요하다.
기름이 부족하면 이동할 수 없다고 할 때 모든 주유소를 방문할 수 있는 출발점의 인덱스를 출력하라.- 출발점이 존재하지 않을 경우
-1을 리턴하며, 출발점은 유일하다.
- 출발점이 존재하지 않을 경우
1. 모두 방문 (4680ms)
class Solution:
def canCompleteCircuit(self, gas: List[int], cost: List[int]) -> int:
for start in range(len(gas)):
fuel = 0
for i in range(start, len(gas) + start):
index = i % len(gas)
can_travel = True
if gas[index] + fuel < cost[index]:
can_travel = False
break
else:
fuel += gas[index] - cost[index]
if can_travel:
return start
return -1
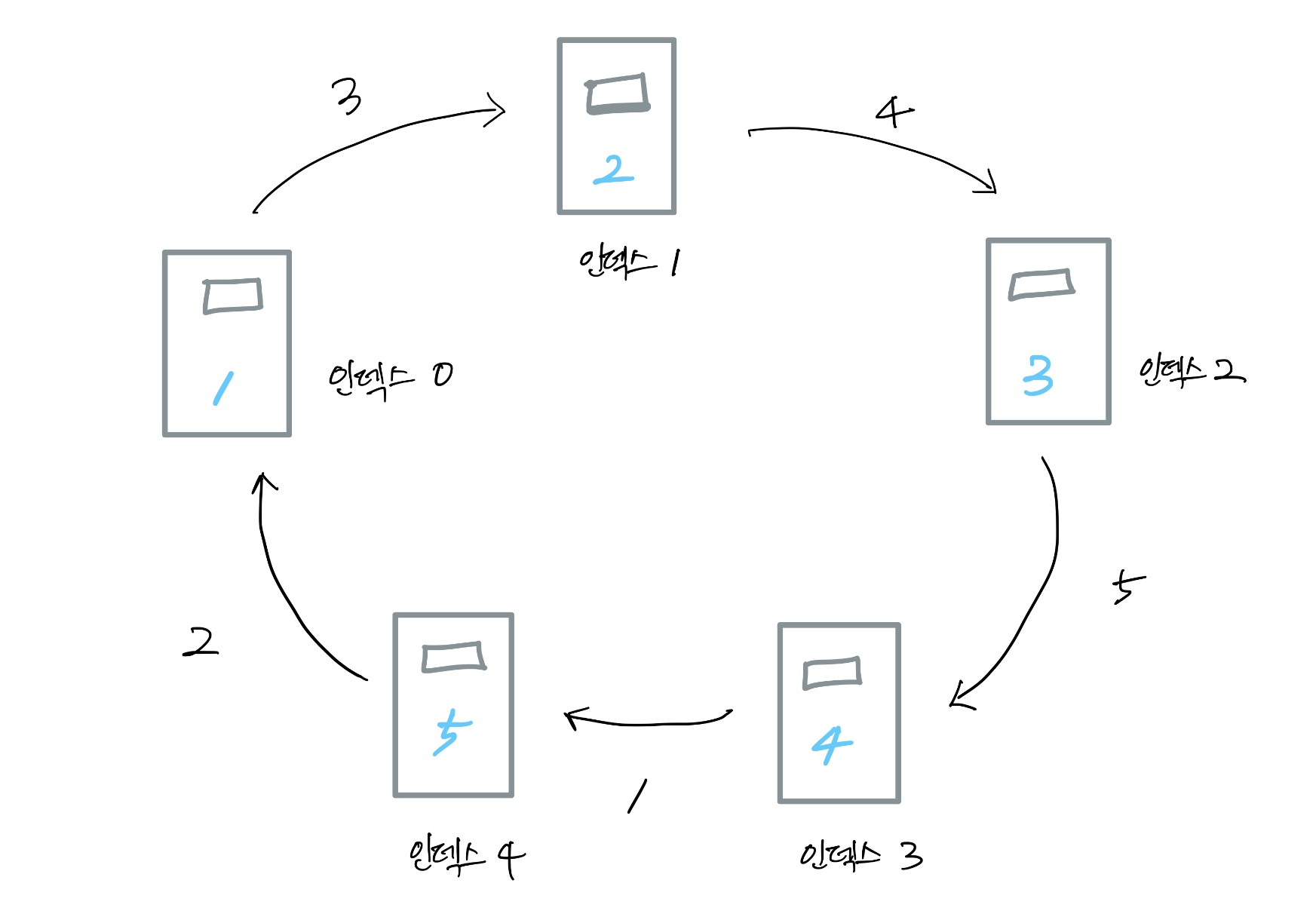
<각 주유소별 보유 기름과 이동 비용>
-
예제에서 정답인
3번 인덱스는 기름을4만큼 충전할 수 있는 지점이다. -
충전 가능한 기름의 양과 인덱스 번호, 이동하는데 필요한 기름의 양을 모두 표기했다.
-
처음부터 한 칸씩 출발점으로 지정하고, 나머지 모든 주유소를 방문하는 방법으로 풀이해보자.
-
주유소의 경로는 원형으로 연결되어 있으므로, 모듈로 연산을 하여 인덱스를 다시
0부터 지정할 수 있게 한다. -
모든 주유소를 방문 가능한지 점검하고, 가능할 경우 이 문제는 출발점이 유일하다는 제약이 있기 때문에, 해당 출발점을 결과로 바로 리턴한다.
- 중간에 끊길 경우 다시 다음번 출발점으로 이 작업을 반복한다.
-
-
루프가 중첩되어 있으므로 O(n2)이다. 좀 더 최적화가 필요하다.
2. 한 번 방문 (56ms)
class Solution:
def canCompleteCircuit(self, gas: List[int], cost: List[int]) -> int:
#모든 주유소 방문 가능 여부 판별
if sum(gas) < sum(cost):
return -1
start, fuel = 0, 0
for i in range(len(gas)):
#출발점이 안되는 지점 판별
if gas[i] + fuel < cost[i]:
start = i + 1
fuel = 0
else:
fuel += gas[i] - cost[i]
return start
-
잘 생각해보면, 전체 기름의 양이 전체 비용보다 클 경우 반드시 전체를 방문할 수 있는 출발점이 존재한다.
- 원래는 여러 곳이 될 수 있겠지만 이 문제에는 출발점이 유일하다는 제약이 있으므로, 여기서는 반드시 한 군데만 존재하게 된다.
-
비용이 더 클 때 리턴해버리면, 이제 반드시 존재하는 경우만 남아 있게 된다.
따라서 전체를 방문하면서 성립되지 않는 경우는 출발점을 한 칸씩 뒤로 밀어낸다.
-
성립되지 않는 지점이 있다면 그 앞은 전부 출발점이 될 수 없다.
-
성립되지 않는 지점을 제외하면서 출발점을 찾는데, 이는 수학에서 귀류법으로 증명하는 것과 유사하다.
-
-
모순을 이끌어내 거짓인 경우를 제외하면, 가능한 지점은 제외하지 못한 지점이고, 자연스럽게 남은 곳이 정답이 된다.
-
두 번의 루프가 한 번으로 줄었다.
-
전체
sum()을 비교하는 구문을 통과했다면 반드시 출발점이 존재하는 경우고, 딱 한 군데만 존재하므로 한 번만 돌면서 확인하는 것으로 충분하다. -
O(n)으로 최적화 했고, 빠른 속도로 실행된다.
- 1번 풀이에 비해 거의 80배 이상 빠른 속도로 실행된다.
-
