83. Majority Element

리트코드

• 과반수를 차지하는(절반을 초과하는) 엘리먼트를 출력하라.

1. 브루트 포스로 과반수 비교 (타임아웃)

class Solution:
    def majorityElement(self, nums: List[int]) -> int:
        
        for num in nums:
            if nums.count(num) > len(nums) // 2
                return num

• 앞에서부터 하나씩 과반수를 넘는지 일일이 체크하다가 과반수를 넘으면 바로 정답으로 처리한다.

• 아쉽게도 타임아웃이 발생한다.

2. 다이나믹 프로그래밍 (180ms)

class Solution:
    def majorityElement(self, nums: List[int]) -> int:
        
        counts = collections.defaultdict(int)
        for num in nums:
            if counts[num] == 0:
                counts[num] = nums.count(num)
                
            if counts[num] > len(nums) // 2:
                return num

• 브루트 포스를 다이나믹 프로그래밍으로 최적화해보자.

• nums.count()로 한 번 카운트를 계산한 값은 저장해서 재활용했다.

  • 만약 계산되지 않았던 값이 들어온다면 항상 0이 될 것이고, 그때만 카운트를 계산하게 될 것이다.

  • 이 풀이는 메모이제이션(Memoization)을 이용한 매우 간단한 다이나믹 프로그래밍 풀이이다.

  메모이제이션(memoization)은 컴퓨터 프로그램이 동일한 계산을 반복해야 할 때, 이전에 계산한 값을 메모리에 저장함으로써 동일한 계산의 반복 수행을 제거하여 프로그램 실행 속도를 빠르게 하는 기술이다. (위키백과)

3. 분할 정복 (252ms)

class Solution:
    def majorityElement(self, nums: List[int]) -> int:
        
        if not nums:
            return None
        if len(nums) == 1:
            return nums[0]
        
        half = len(nums) // 2
        a = self.majorityElement(nums[:half])
        b = self.majorityElement(nums[half:])
        
        return [b,a][nums.count(a) > half]

• 병합 정렬은 분할 정복의 진수를 보여주는 알고리즘인데, 이 문제는 병합 정렬과 매우 유사한 방식으로 풀이할 수 있다.

  • 쪼갠 다음 정렬해서 각각의 엘리먼트를 전부 리턴하는 병합 정렬과 달리, 여기서는 과반수 후보군에 해당하는 엘리먼트만 리턴하면서

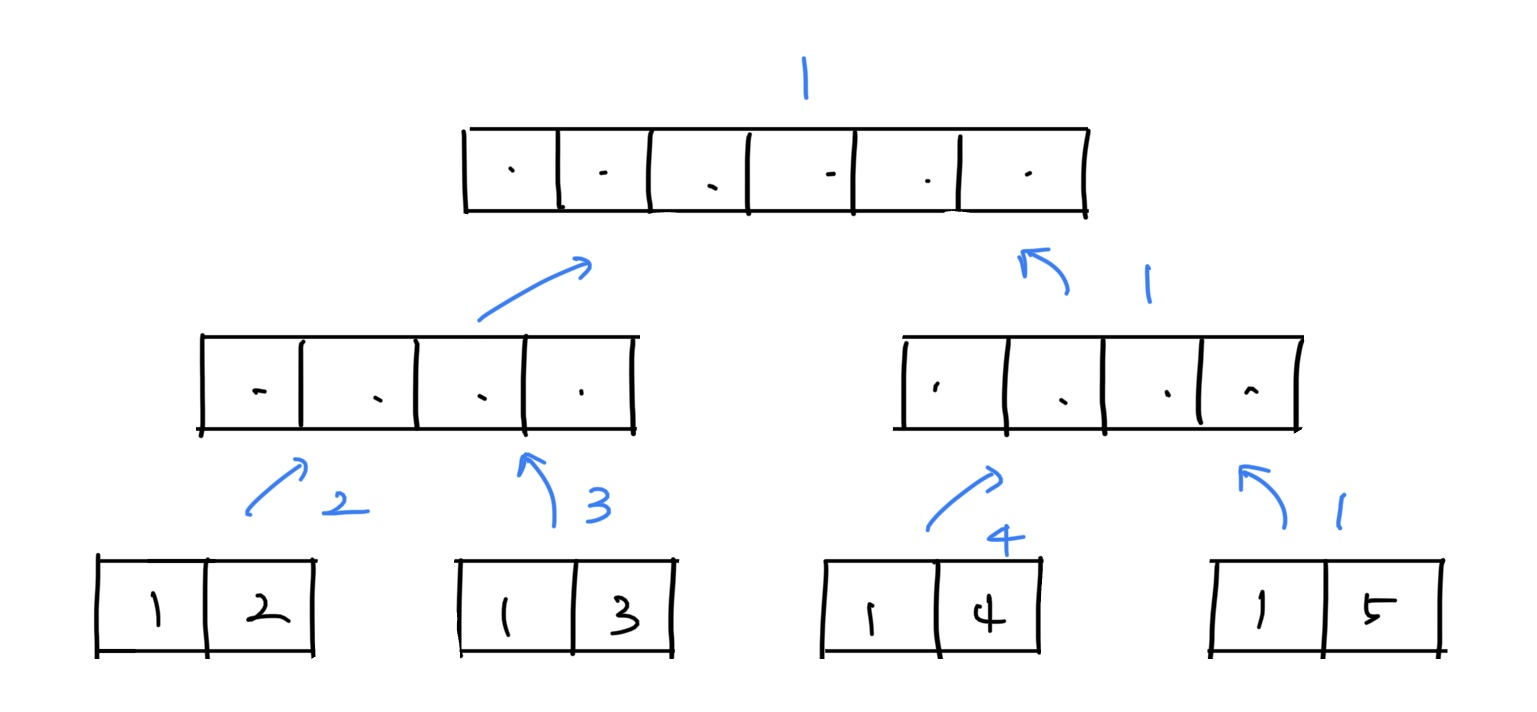
  • 다음 그림과 같이 계속 위로 올려주면(즉 백트래킹하면) 최종적으로 정답이 남게 된다.

  

• 먼저 분할을 시도한다. a와 b는 각각 최소 단위로 쪼개질 것이다.

  • 그렇게 하기 위해서는 상단에 끊어서 리턴해주는 부분이 필요하다.

  • 리턴해주면, 최소 단위로 쪼개질 때 해당하는 값을 리턴하게 될 것이다.

• 다음으로 백트래킹될 때 처리하는 부분, 즉 정복에 해당하는 부분을 구현한다.

  • a가 만약 현재 분할된 리스트 nums에서 과반수를 차지한다면 해당 인덱스는 1이 될 것이고, [b, a][1]이 되어 a를 리턴할 것이다.

    • 과반수인 엘리먼트 이외에는 b를 리턴한다.

  • 만약 앞서 그림에서 [2,2,1]이 있을 때, 각각 2와 1이 백트래킹 되고, 2가 과반수를 차지하므로 [1, 2][1]이 되어, 2를 리턴하게 될 것이다.

    • 최종적으로 루트에 이르러서는 양쪽 모두 2,2가 리턴되었고, 이 경우는 예외 없이 2가 정답이다.

  • 만약 입력값이 [1,2,1,3,1,4,1,1]일 경우에는 공교롭게도 2,3,4만 리턴되어서 정답을 찾을 수 없는 경우가 존재하지 않을까? 그렇지 않다.

    • 과반수를 차지하는 엘리먼트를 찾는 문제이므로, 이 경우 비둘기집 원리에 따라 반드시 [1,1]이 함께 위치하는 분할이 존재한다.

    • 따라서 1은 최소 한 번 이상 반드시 리턴될 것이고, 계속 상위 분할에서 과반수를 넘어설 것이므로 끝까지 살아남아 최종적으로 1을 리턴하게 될 것이다.

    

4. 파이썬다운 방식 (176ms)

class Solution:
    def majorityElement(self, nums: List[int]) -> int:
        return sorted(nums)[len(nums) // 2]

• 정렬하여 가운데를 지정하면 반드시 과반수 이상인 엘리먼트일 것이다.

  • 매우 직관적이며 쉬운 알고리즘이다.

  • 파이썬다운 방식이 가장 쉬우면서도 빠르다.