
1. ER(Entitiy Relationship) Model
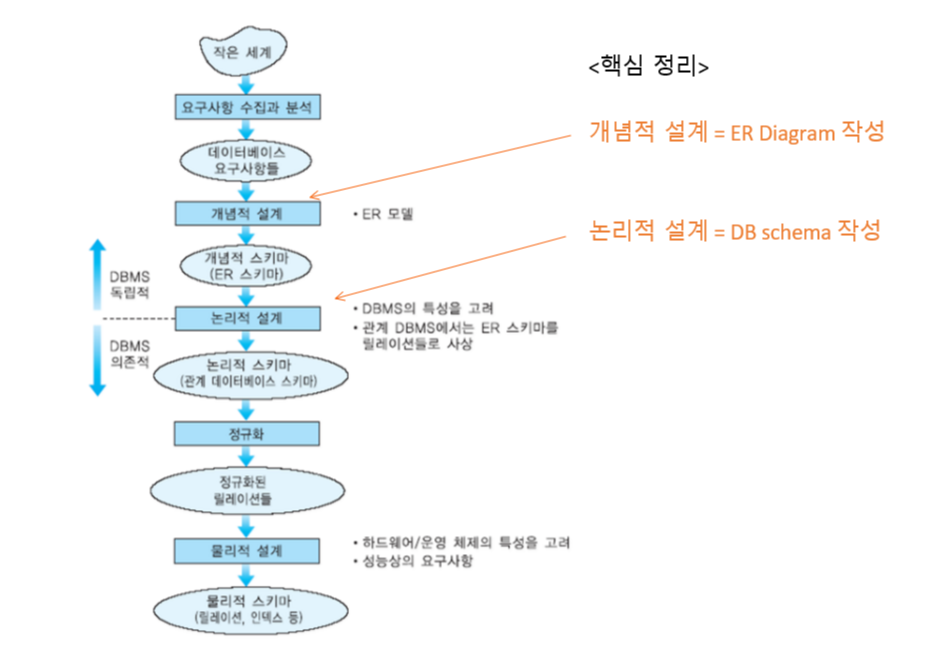
개념적 설계 단계 (데이터베이스 설계의 2단계)
-
ER Model (상기 단계에서 2 단계에 해당한다.)
- 초기의 고수준(개념적) 데이터베이스 설계를 표현하는데 사용되는 모델
- ER Model은 쉽게 관계 데이터 모델로 사상된다.
- 데이터베이스 설계를 용이하게 하기 위해서 P.P Chen이 1976년에 제안한 이후, 점차 강화되었으며, 현재 EER(Enhanced Entitiy Relationship) 모델이 데이터베이스 설계 과정에 널리 사용되고 있다.
-
기본적인 구문으로는 엔티티, 관계, 애트리뷰트이 있다.
-
기타 구문으로는 카디날리티 비율, 참여 제약조건 등
- 초기의 고수준(개념적) 데이터베이스 설계를 표현하는데 사용되는 모델
-
ER Model의 장점
(1) 적은 노력으로 쉽게 배울 수 있음
(2) 전문가가 아니어도 이해하기 쉬움
(3) 자연어보다는 좀 더 정형적임
(4) 구현에 독립적이어서 Database 설계자들이 최종 사용자들과 의사 소통을 하는데 적합함
-
기타 사항
-
ER Model을 기반으로 만들어진 다수의 CASE 도구(예, ERWin, DataArchitect, PowerBuilder 등)
-
이런 도구들은 ER 설계를 자동적으로 Sybase, Oracle, Infomix, DB2 등의 DDL로 자동 변환됨
-
ER 모델링은 현재는 Database 설계를 위한 다소 구형 그래픽 표기법으로
현재, 대규모 기업의Database 설계에서는 UML(Unified Modeling Language)을 사용
-
엔티티 (Entity)
-
하나의 엔티티는 사람, 장소, 사물, 사건 등과 같이 독립적으로 존재하면서 고유하게 식별이 가능한 실세계의 객체
-
사원처럼 실체가 있는 것도 있지만 생각이나 개념과 같이 추상적인 것도 있다.

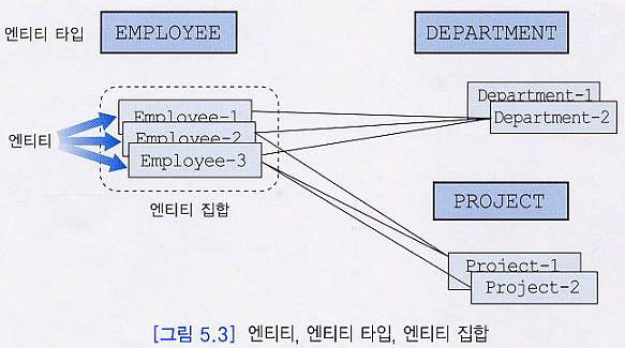
엔티티 타입 (Entity Type, 속성의 집합을 “타입”이라고 명함)
-
엔티티 타입
:관계 모델의 관계의 내포(Schema) 에 해당- 동일한 애트리뷰트들을 가진 에티티들의 틀
-
엔티티 집합
: 관계 모델의 관계의 외연(Instances, Tuples)에 해당한다.- 동일한 애트리뷰트들을 가진 엔티티들의 모임
-
엔티티들
: 엔티티 타입(or 엔티티 집합)들에 따라 분류된다.- 하나의 엔티티는 한 개 이상의 엔티티 집합에 속할 수 있다.
-
단, ER Diagram에서는 엔티티 타입과 엔티티 집합을 엄격하게 구분할 필요는 없다.
- 즉, 스키마와 인스턴스를 엄격히 구분하지 않는다는 의미
-
ER Diagram에서 엔티티 타입은 직사각형으로 나타낸다.
강한 엔티티 타입 vs 약한 엔티티 타입
-
강한 엔티티 타입
-
강한 엔티티 타입(정규 엔티티 타입)은 독자적으로 존재하며
-
엔티티 타입 내에서 자신의 키 애트리뷰트를 사용하여 고유하게 엔티티들을 식별할 수 있는 엔티티 타입을 의미한다.
-
약한 엔티티 타입을 소유한다는 개념으로 소유 엔티티 타입 이라고도 불리운다.
-
-
약한 엔티티 타입
-
약한 엔티티 타입은 키를 형성하기에 충분한 애트리뷰트들을 갖지 못한 엔티티 타입이다. (꼭 있지 않아도 되지만, 있으면 유익)
-
약한 엔티티 타입이 존재하려면, 소유 엔티티 타입(Owner entity type)이 있어야한다.
- 강한 엔티티 타입이 소유 엔티티 타입이 될 수 있다.
-
소유(강한) 엔티티 타입의 키 애트리뷰트를 결합해야만 고유하게 약한 엔티티 타입의 엔티티들을 식별할 수 있다.
- 약한 엔티티 타입에게 키 애트리뷰트를 제공하는 엔티티 타입
- 따라서 식별 엔티티 타입(Identifying entity type)이라고도 부름
-
ER Diagram에서 약한 데이터 타입은 이중선 직사각형으로 표시한다.
-
약한 엔티티 타입의 부분 키는 점선 밑줄을 그어 표시
-
부분 키(partial key)
- 부양 가족의 이름(ex) 김철수)처럼 한 사원에 속한 부양가족 내에서는 서로 다르지만, 회사 전체 사원들의 부양 가족들 전체에서는 같은 경우(ex) 여러명의 김철수)가 생길 수 있는 애트리뷰트
-
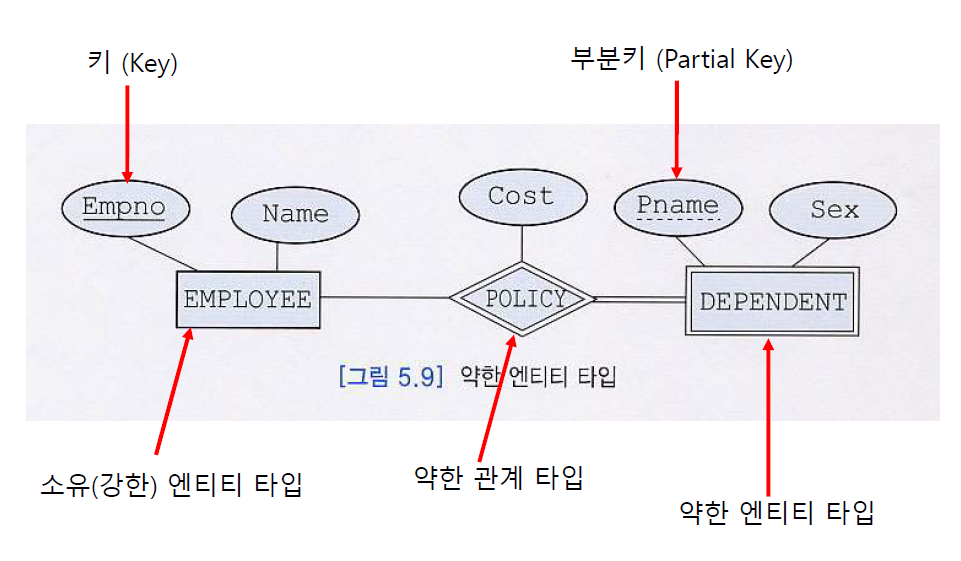
애트리뷰트
-
하나의 엔티티는 연관된 애드리뷰트들의 집합으로 설명된다.
- 예: 사원 엔티티 는 사원번호, 이름, 직책, 급여 등의 애트리뷰트를 갖는다.
-
한 애트리뷰트의 도메인은 그 애트리뷰트가 가질 수 있는 모든 가능한 값들의 집합을 의미한다.
-
예: 사원번호는 1000부터 9999까지의 값을 가진다.
-
다른 예로는, 사원번호는 integer 도메인을 쓰겠다 등
-
-
여러 애트리뷰트가 동일한 도메인을 공유할 수 있다.
- 예: 사원번호와 부서번호가 4자리 정수를 가질 수 있다.
-
키(key) 애트리뷰트 는 한 애트리뷰트 또는 애트리뷰트들의 모임으로서 한 엔티티 타입 내에서 각 엔티티를 고유하게 식별한다.
-
ER Diagram에서 기본 키(Prime Key)에 속하는 애트리뷰트는 밑줄을 그어 표시한다.
-
애트리뷰트는 요구사항 명세에서 명사나 형용사로 표현된다.
-
엔티티와 애트리뷰트의 차이점은 엔티티는 독립적인 의미를 갖는데 반해서 애트리 뷰트는 독립적인 의미를 갖지 않는다는 것이다.
-
ER Diagram에서 애트리뷰트는 타원형으로 나타낸다.
-
애트리뷰트와 엔티티 타입은 실선으로 연결한다.
①단순 애트리뷰트(simple attribute)
-
더 이상 다른 애트리뷰트로 나눌 수 없는 애트리뷰트
-
ER Diagram에서 실선 타원으로 표현
-
ER Diagram에서 대부분의 애트리뷰트는 단순 애트리뷰트
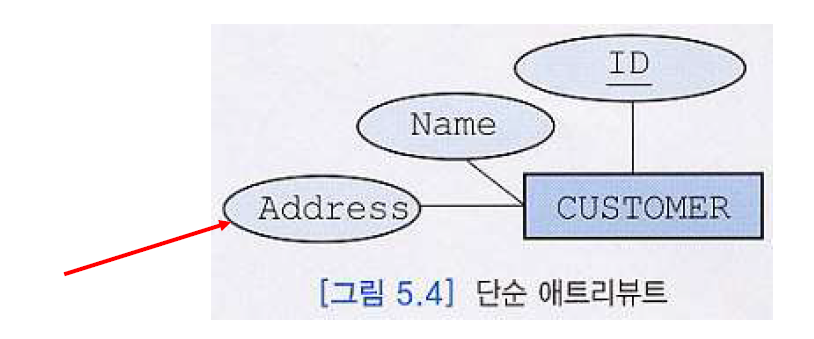
-
밑줄이 그어져 있는 것은 키 애트리뷰트이다.
- 그림에서의 ID
②복합 애트리뷰트(composite attribute)
-
두 개 이상의 애트리뷰트로 이루어진 애트리뷰트
-
동일한 엔티티 타입이나 관계 타입에 속하는 애트리뷰트들 중에서 밀접하게 연관된 것을 모아놓은 것
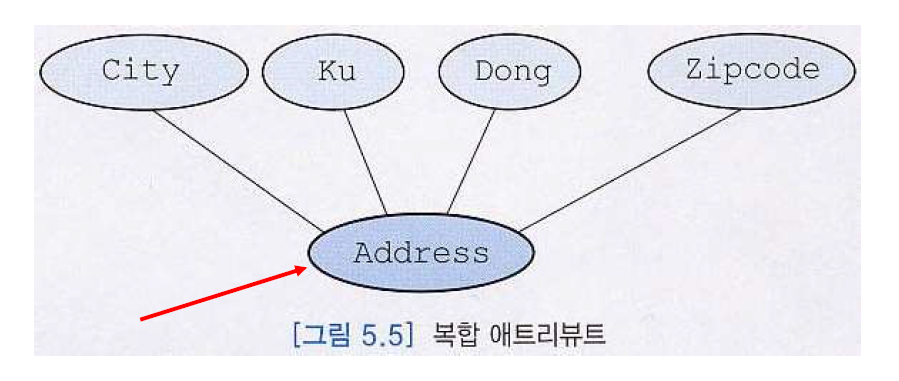
- 여기서 Adress가 복합 애트리뷰트
③단일 값 애트리뷰트(single-valued attribute)
- 각 엔티티 마다, 정확하게 하나의 값(unique value)을 갖는 애트리뷰트
-
단일 값 애트리뷰트는 ER Diagram에서 단순 애트리뷰트와 동일하게 표현된다.
-
예: 사원의 사원번호 애트리뷰트는 어떤 사원도 두 개 이상의 사원번호를 갖지 않으므로 단일 값 애트리뷰트
-
키 애트리뷰트 같은 개념
-
-
ER Diagram에서 대부분의 애트리뷰트는 단순 애트리뷰트
④다치 애트리뷰트(multi-valued attribute)
-
각 엔티티마다 여러 개의 값을 가질 수 있는 애트리뷰트
-
예: 여러가지 색깔을 가진 자동차 등
-
ER Diagram에서 이중선 타원으로 표현
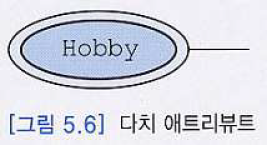
- 여기서 Hobby는 레고조립, 영화감상 등 여러개 값을 가질 수 있음
⑤저장된 애트리뷰트 (stored attribute)
-
다른 애트리뷰트와 연관성이 없이 독립적으로 존재하는 애트리뷰트
-
예: 사원 엔티티 타입에서 사원 이름, 급여는 다른 애트리뷰트와 연관 관계가 없이 독립적으로 존재하므로 저장된 애트리뷰트에 속한다.
-
예: 시(city), 도(province) 등은 주소(address) 애트리뷰트와 연관되며, 독립적으로 존재하지 않으므로 저장된 애트리뷰트에 속하지 않는다.
-
-
ER Diagram에서 대부분의 애트리뷰트는 저장된 애트리뷰트
-
ER Diagram에서 단순 애트리뷰트와 동일하게 표현된다.
⑥유도된 애트리뷰트(derived attribute)
-
다른 애트리뷰트의 값으로부터 얻어진 애트리뷰트
-
예: 주민등록번호로부터 나이를 얻어낼 수 있다.
-
유도된 애트리뷰트는 관계 데이터베이스에서 관계의 애트리뷰트를 포함시키지 않는 것이 좋다.
- 예: 나이와 같이 매년 변화되는 것들은 넣지 않는 것이 좋다.
-
ER Diagram에서 점선 타원으로 표현한다.
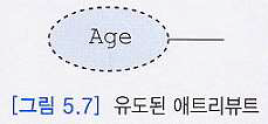
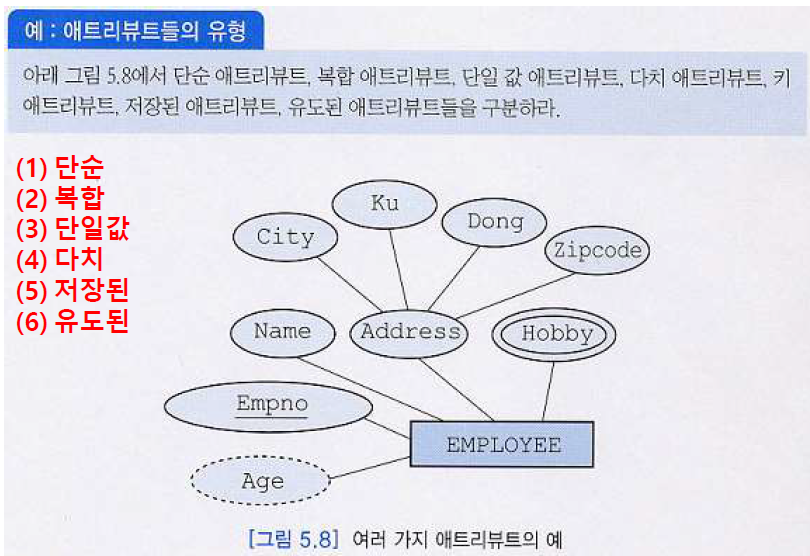
- 단순: EMPLOYEE, Name, City, Ku... 등
- 복합: Address
- 단일값: Empno(Employee number)
- 다치: Address
- 저장된: EMPLOYEE, Hobby
- 유도된: Age
관계와 관계 타입
-
관계는 엔티티들 사이에 존재하는 연관이나 연결로서, 두 개 이상의 엔티티 타입들 사이의 사상으로 생각할 수 있다.
-
관계 집합은 동질의 관계들의 집합
-
관계 타입은 동질의 관계들의 틀
-
요구사항 명세에서는 흔히, 동사는 ER Diagram에서 관계로 표현된다.
-
ER Diagram에서 다이아몬드로 표기한다.
-
관계 타입이 서로 연관시키는 엔티티 타입들을 관계 타입에 실선으로 연결한다.
-
-
관계 집합과 관계 타입을 엄격하게 구분할 필요는 없다.

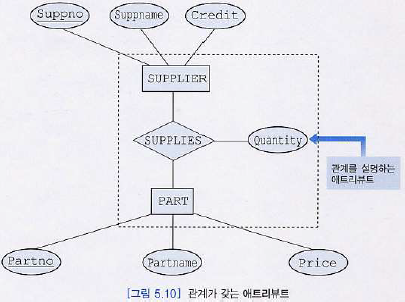
관계의 애트리뷰트
- 관계 타입은 관계의 특징을 기술하는 애트리뷰트들을 가질 수 있다.
- 관계 타입은 키 애트리뷰트를 갖지 않는다.
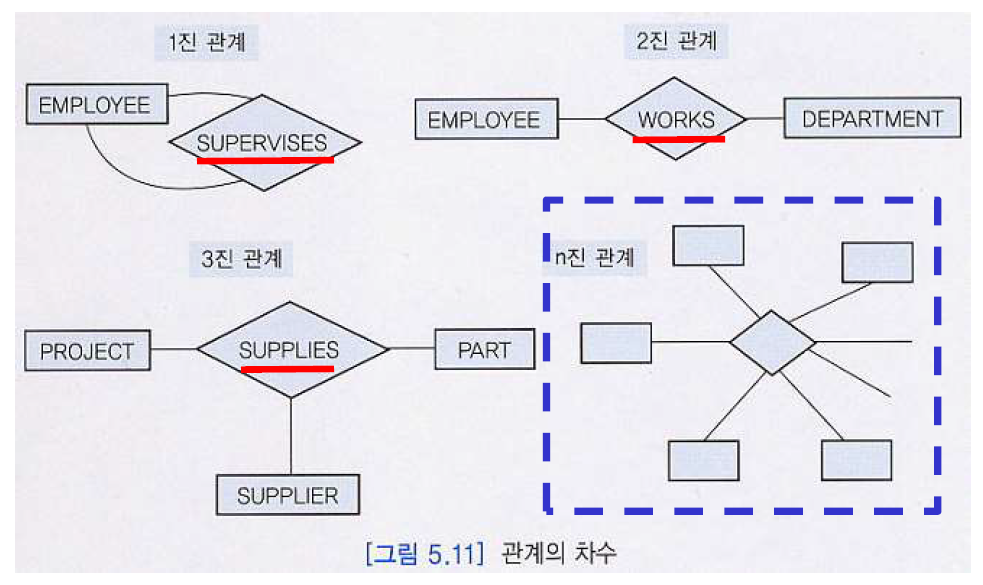
차수(degree)
-
관계의 차수는 관계로 연결된, 엔티티 타입들의 연관 개수를 의미한다.
-
실세계에서 가장 흔한 관계는 두 개의 엔티티 타입을 연결하는 2진 관계이다.
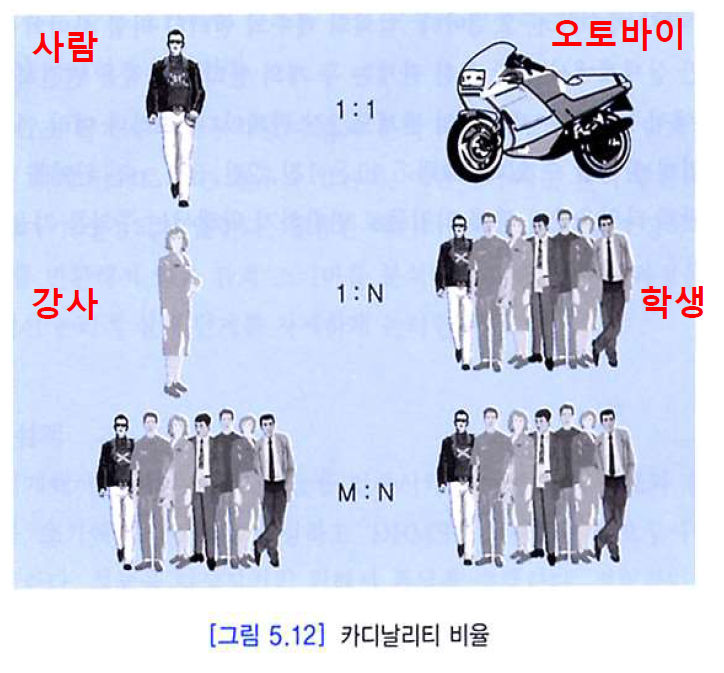
카디날리티 비율 (첫 번째 제약 조건)
-
카디날리티 비율은 한 엔티티가 참여할 수 있는 관계의 수를 나타낸다.
-
관계 타입에 참여하는 엔티티들의 가능한 조합을 제한한다.
-
관계를 흔히 1:1, 1:N, M:N,으로 구분한다.
-
카디날리티에 관한 정보는 간선 위에 나타낸다.
1:1 관계
-
E1의 각 엔티티가 정확하게 E2의 한 엔티티와 연관되고,
E2의 각 엔티티가 정확하게 E1의 한 엔티티와 연관되면,
이 관계를 1:1 관계라고 한다.
-
예: 각 사원에 대해 최대한 한 개의 PC가 있고,
각 PC에 대해 최대한 한 명의 사원이 있으면,
고유 사원과 고유 PC간의 관계는 1:1 관계
1:N 관계
- E1의 각 엔티티가 E2의 임의의 개수의 엔티티와 연고나되고,
E2의 각 엔티티는 정확하게 E1의 한 엔티티와 연관괴면,
이 관계를 1:N 관계라고 한다. - 예: 각 사원에 대해 최대한 한 대의 PC가 있고,
각 PC에 대해 여러 명의 사원들이 있으면,
고유 PC와 여러 사원 간의 관계는 1:N 관계
M:N 관계
- 한 엔티티 타입에 속하는 임의의 개수의 엔티티가,
다른 엔티티 타입에 속하는 임의의 개수의 엔티티와 연관되면,
이 관계를 M:N 관계라고 한다. - 예: 각 사원에 대해 여러 대의 PC가 있고,
각 PC에 대해 여러 명의 사원들이 있으면,
여러 사원과 공용 PC 간의 관계는 M:N 관계
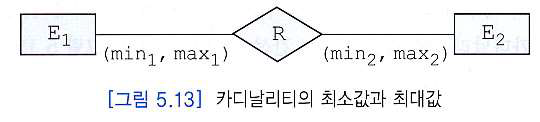
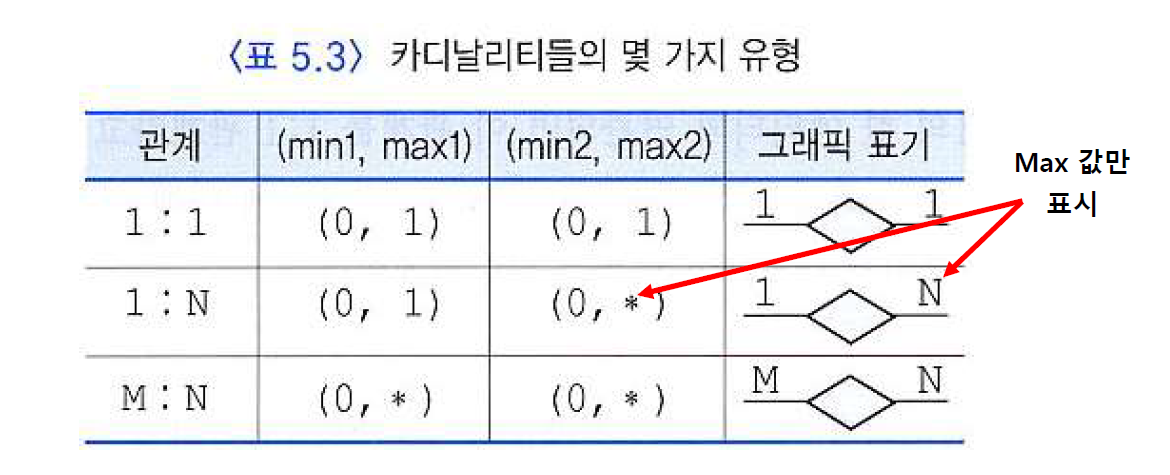
카디날리티 비율의 최솟값과 최댓값
-
ER Diagram에서 관계 타입과 엔티티 타입을 연결하는 실선 위에 다음과 같은 형태로 표기
(min, max) -
어떤 관계 타입에 참여하는 각 엔티티 타입에 대하여
-
min: 이 엔티티 타입 내의 각 엔티티는 적어도 min 번 관계에 참여함을 의미
-
max: 이 엔티티 타입 내의 각 엔티티는 최대한 max 번 관계에 참여함을 의미
-
-
min=0 은 어떤 엔티티가 반드시 관계에 참여해야 할 필요는 없음을 의미한다.
-
max=* 는 어떤 엔티티가 관계에 임의의 수만큼 참여할 수 있음을 의미한다.
역할(role)
-
관계 타입의 의미를 명확하게 하기 위해 사용된다.
-
특히 하나의 관계 타입에 하나의 엔티티 타입이 여러 번 나타나는 경우에는 반드시 역할을 표기해야 한다.
-
관계 타입의 간선 위에 표시
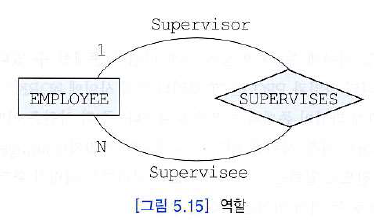
- recursive한 경우 role을 적어놓는 것은 더욱 이해하는 데 도움이 된다.
전체참여와 부분참여(두 번째 제약조건)
-
전체 참여는 어떤 관계에 엔티티 타입 E1의 모든 엔티티들이 관계 타입 R에 의해서 어떤 엔팉 타입 E2의 어떤 엔티티와 연관되는 것을 의미
-
약한 엔티티 타입은 항상 관계에 전체 참여한다.
-
전체 참여는 ER Diagram에서 이중 실선으로 표시한다.
-
- 부분 참여는 어떤 관계에 엔티티 타입 E1의 일부 엔티티만 참여하는 것을 의미
- (1)카디날리티 비율과 함께 (2)참여 제약조건은 관계에 대한 중요한 제약조건

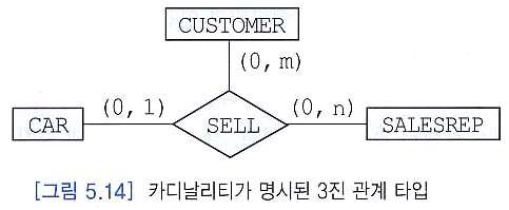
다중 관계
- 두 엔티티 타입 사이에 두 개 이상의 관계 타입이 존재할 수 있다.
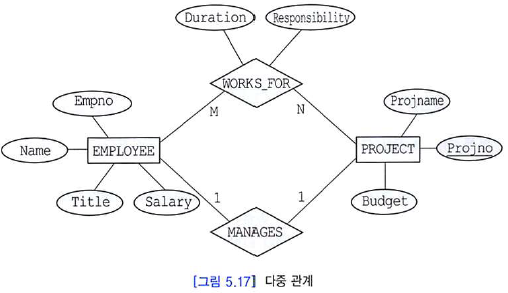
순환적 관계
- 하나의 엔티티 타입이 동일한 관계 타입에 두번 이상 참여하는 것
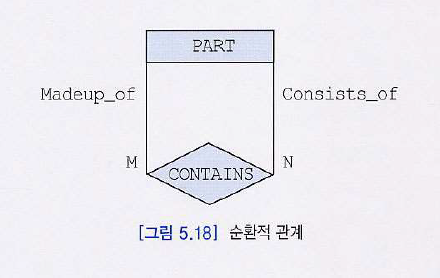
➕ (참고)ER Schema를 작성하기 위한 지침
-
다치 애트리뷰트 → 엔티티로 분류해야 한다.
-
엔티티에는 애트리뷰트들이 직접적으로 연관된 애트리뷰트들을 한정해서 붙인다.
-
가능한 한 복합 식별자를 피한다.
-
관계는 일반적으로 독자적으로 존재할 수 없지만, 엔티티 타입과 관계 타입을 절대적으로 구분하는 것은 어렵다.
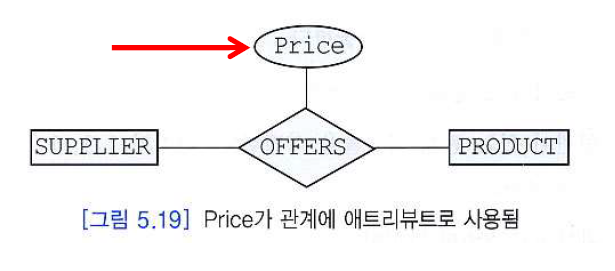
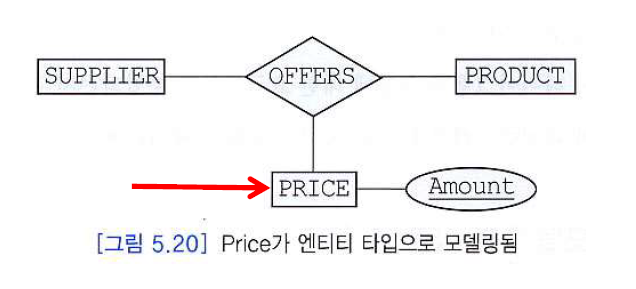
데이터베이스 설계 과정
-
응용의 요구사항을 수집하여 기술
-
사전 결정 사항
- 응용과 연관이 있는 엔티티 타입들을 식별하여 결정
- 응용과 연관이 있는 관계 타입들을 식별하여 결정
- 관계가 1:1, 1:N, M:N 중에서 어느 것에 해당하는지 결정
- (응용을위한)ER Schema Diagram을 작성
- 엔티티 타입에 필요한 애트리뷰트 들을 식별하여 그림을 그리고,
- 관계 타입들에 필요한 애트리뷰트들을 식별하여 그림을 그리고,
- 각 애트리뷰트가 가질 수 있는 값들의 집합을 고려하여 카더널리티와 참여 방법 의 관계성을 적는다.
- 애트리뷰트들 중에서 엔티티 타입들을 위한 기본 키를 식별한다.
-
ER Schema Diagram이 응용에 대한 요구사항에 부합되는지 최종 검사한다.
-
ER Schema Diagram을 각종 DBMS에서 사용되는 데이터베이스 모델로 변환한다.
<ER 표기법의 요약>
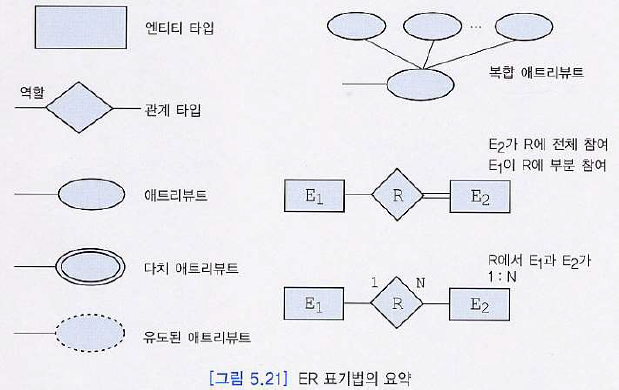
➕(참고만) ER Model의 또 다른 표기법
-
본 장에서 사용한 표기법으로 수 십개 이상의 애트리뷰트가 엔티티 타입에연결된 Diagram을 나타내려면 매우 불편하고 공간을 많이 차지
-
ERWin등의 CASE 도구들에서는 새발(crow-feet)표기법이 흔히 사용됨
-
새발 표기법에도 여러가지 변형들이 존재한다.

