응력-변형률 곡선(Stress-Strain curve, SS curve) 란?

출처, 출처2, 출처3

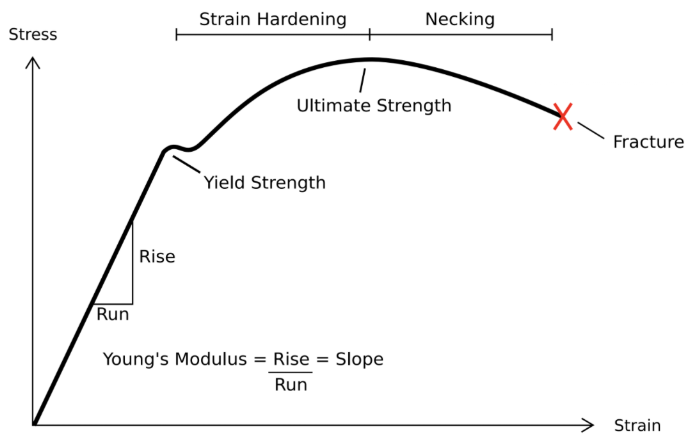
1. 응력-변형률 곡선(Stress-Strain curve, SS curve) 이란?

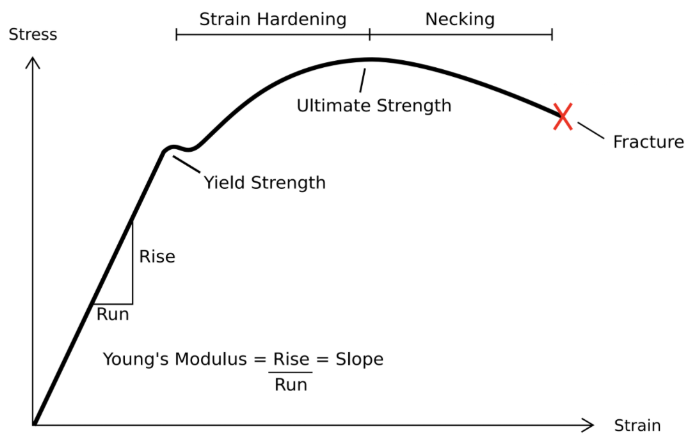
• 응력-변형률 곡선은 재료가 외력을 받을 때 나타나는 기계적 특성을 나타낸 차트입니다.

• 이 곡선은 재료의 강도, 변형 저항성, 연성 등을 이해하는 데 필수적입니다.

• 시편에 가하는 힘(Stress)에 따라서 변형 (Strain)되는 것을 나타냄.

  • x축은 Strain (변형률)

  • y축은 Stress (응력)

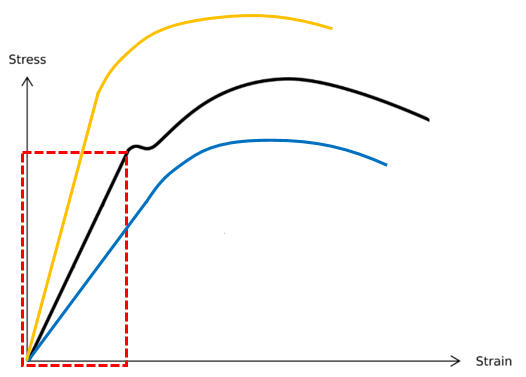
• 탄성 영역 (Elastic Region)이란?

  • 그래프에서 탄성 영역은 소재가 늘어났다가 다시 원래의 상태로 복구되는 부분을 말합니다.

  • 이 영역에서는 소재가 원래 형태로 돌아가려는 성질을 보여줍니다.

• 탄성 영역의 기울기(Young's Modulus, E)

  • 그래프의 기울기는 영률(Young's Modulus)을 나타내며, 아래와 같은 특징이 있습니다.

    • 기울기가 클수록 변형을 일으키기 위해 더 큰 힘이 필요합니다.

    • 변형이 충분히 일어난 뒤 풀림(Springback)의 양도 커집니다.

    • 풀림이란 소재가 원래의 상태로 돌아가려는 성질을 의미하며, 가한 힘이 많을수록 풀림의 크기도 커집니다. (풀림 현상은 소성 영역에서 더 자세히 설명됩니다.)

영률(Young’s Modulus)은 재료의 탄성 영역에서 응력(힘)과 변형률(늘어나는 정도) 사이의 비례 상수로, 재료가 얼마나 단단하고 변형에 저항하는지를 나타내는 물리적인 값입니다.

• 쉽게 말하면, ”재료가 변형되지 않고 얼마나 버티는가”를 숫자로 나타낸 것입니다.
  • 영률이 클수록 재료는 더 단단하고, 변형되기 어려우며, 작은 응력에서도 원래 상태로 잘 복귀합니다.
    $E = \frac{\text{응력(Stress)}}{\text{변형률(Strain)}}$

• 소재 성형 시의 영향

  • 기울기가 클수록 (가파를수록: 주황색 커브)

    • 변형을 위해 더 큰 힘이 필요하며, 변형 이후 풀림이 더 커집니다.

    • 성형 작업 시 더 높은 압력이 필요하고, 정밀한 공차를 얻기 위해 추가적인 작업이 요구됩니다.

    • 소재의 편차로 인해 제품 품질이 들쭉날쭉할 가능성이 있습니다.

  • 기울기가 작을수록 (완만할수록: 파란색 커브)

    • 변형을 일으키기 위한 힘은 작아 작업이 용이합니다.

    • 소성 변형으로 진입하기 쉬우며, 성형 작업에 적합합니다.

    • 하지만 변형 이후 풀림이 여전히 발생하므로, 설계 치수와 약간의 차이가 생길 수 있습니다.

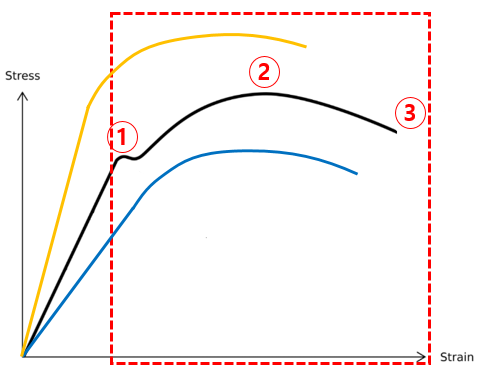
• 소성 영역 (Plastic Region)

  • 소성 영역은 재료가 항복점을 넘어 영구적으로 변형이 시작되는 구간입니다.

  • 이 영역에서는 외력을 제거해도 원래 상태로 복구되지 않으며, 변형이 영구적으로 남습니다.

• 소성 영역에서의 주요 지점들은 아래와 같습니다.

  ① 지점: 항복 응력 (Yield Stress)

  • 소재가 소성 변형을 시작하기 위해 필요한 최소한의 응력.
  • 소재가 이 응력 범위를 초과해야 비로소 완전한 변형이 일어납니다.

  ② 지점: 인장 강도 (Ultimate Tensile Strength, UTS)

  • 소재가 견딜 수 있는 최대 응력 지점.

  • 인장 강도는 UTS, TS, US 등의 다양한 용어로 불리니 혼동하지 않도록 주의해야 합니다.

  ③ 지점: 파단점 (Fracture Point)

  • 이 지점 이후로 소재는 견디는 힘이 약해지며, 국부적인 변형 현상(Necking)이 시작됩니다.

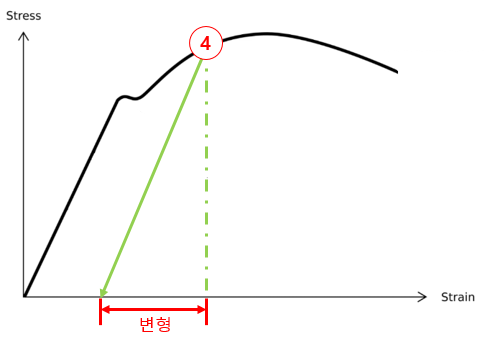
• 스프링백과 소재의 탄성 복원

  ④ 스프링백 (Springback)

  • 외력을 제거했을 때, 소재가 탄성 변형 에너지에 의해 원래 상태로 되돌아가려는 현상입니다.

  • 이는 소재의 탄성계수(Elastic Modulus)의 Slope에 따라 나타나며, 외력이 제거되면서 복원력이 작용해 발생합니다.

• 발생 원인

  • 내부 잔류 응력: 응력이 완전히 해소되지 않은 상태로 인해 스프링백이 일어납니다.

  • 가공 중 절단

    • 소재를 자르면 내부의 잔류 응력이 풀리고 강성이 약화되면서 스프링백이 더 크게 나타날 수 있습니다.

    • 가공 공정에서 절단 방식이나 스트레스 분포 설계가 중요합니다.

정의

• 응력(Stress): 단위 면적당 가해지는 힘

  • $sigma = \frac{F}{A}$ [단위: Pa(파스칼)]

• 변형률(Strain): 재료 길이의 상대적 변화

  • $\epsilon = \frac{\Delta L}{L_0}$ (단위 없음)

응력-변형률 곡선은 실험적으로 재료에 힘을 가하는 인장 시험을 통해 얻어지며,
변형률에 따른 응력의 변화를 곡선으로 나타냅니다.

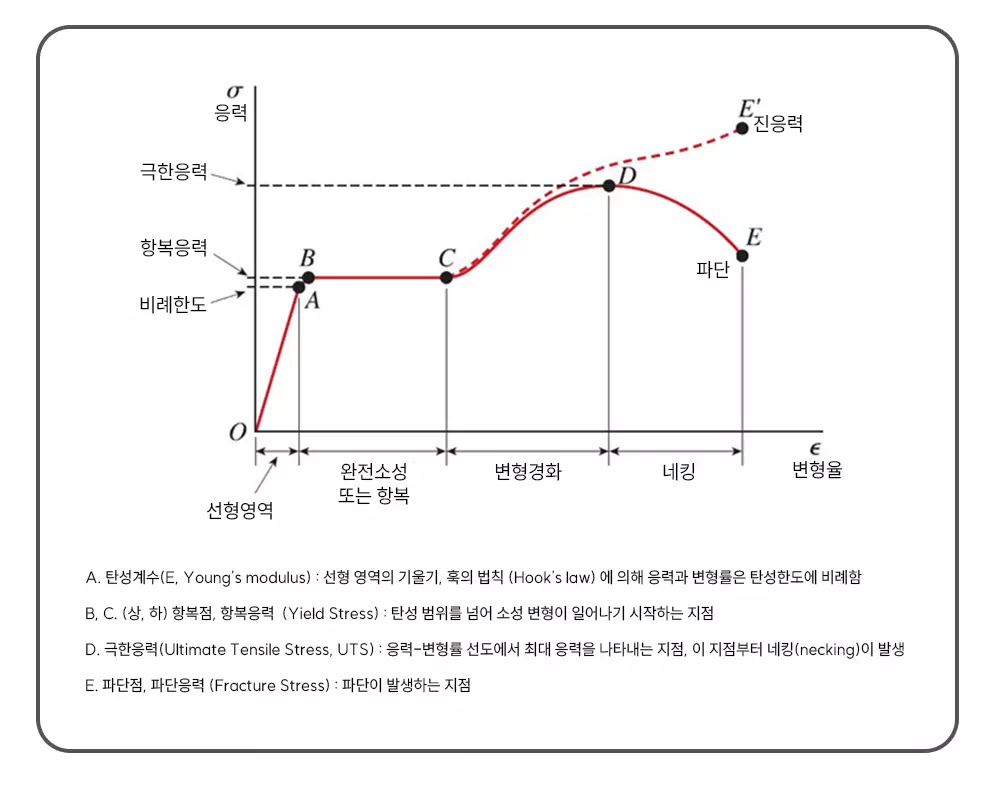
주요 구간과 특징

1. 비례한도(Proportional Limit)

   • 응력과 변형률이 선형적 관계를 가지는 구간.

   • 비례 관계는 훅의 법칙(Hooke's Law)에 의해 설명됨.

     $E = \frac{\sigma}{\epsilon}$

     • 여기서 E는 탄성계수(Young's modulus).

2. 탄성 한도(Elastic Limit)

   • 외력을 제거하면 재료가 원래 상태로 복원 가능한 영역.

   • 이때까지는 탄성 변형(Elastic Deformation).

3. 항복점(Yield Point)

   • 재료가 소성 변형(Plastic Deformation)을 시작하는 지점.

   • 이 지점부터 외력을 제거해도 재료는 원상 복구되지 않음.

   • 항복 강도 ($\sigma_Y$): 항복점에서의 응력 값.

4. 소성 변형(Plastic Deformation)

   • 재료가 영구 변형을 겪는 구간.

   • 응력이 증가하면서 변형은 더 뚜렷해짐.

5. 최대 강도(Tensile Strength)

   • 재료가 견딜 수 있는 최대 응력 점.

   • 이후 국부적 결함이 발생하며 목 현상(Necking)이 나타남.

6. 파단점(Fracture Point)

   • 재료가 파괴되는 지점.

   • 파단점까지의 변형률은 연성(Ductility)을 나타냄.

응력-변형률 곡선의 주요 의미

• 탄성 영역 (Elastic Region)

  • 하중 제거 시 재료가 복원됨.

  • 선형 관계: 기울기 = 탄성계수(Young’s Modulus, E).

• 소성 영역 (Plastic Region)

  • 재료가 탄성 한계를 넘어 영구 변형 발생.

  • 큰 변형률을 보이는 연성 재료와 바로 파괴되는 취성 재료로 나뉨.

대표적인 응력-변형률 곡선 유형

1. 연성 재료(예: 강철, 알루미늄):

   • 항복점 이후 소성 변형이 크며, 변형률이 높음.

2. 취성 재료(예: 세라믹, 유리):

   • 탄성 영역만 존재하며, 변형 없이 바로 파단.

3. 고분자 재료(예: 플라스틱):

   • 점탄성 거동이 뚜렷하며, 항복 이후 큰 연신율을 가짐.

응용

• 응력-변형률 곡선은 재료 공학, 구조 설계 등에서 필수적으로 활용되는 중요한 도구입니다.

  • 재료 선택: 항복 강도와 연성 등을 기준으로 적합한 재료 선정.

  • 구조 설계: 구조물의 안전성과 최대 하중을 고려한 설계.

  • 신소재 개발: 새 재료의 물성 평가와 설계 기준 수립.