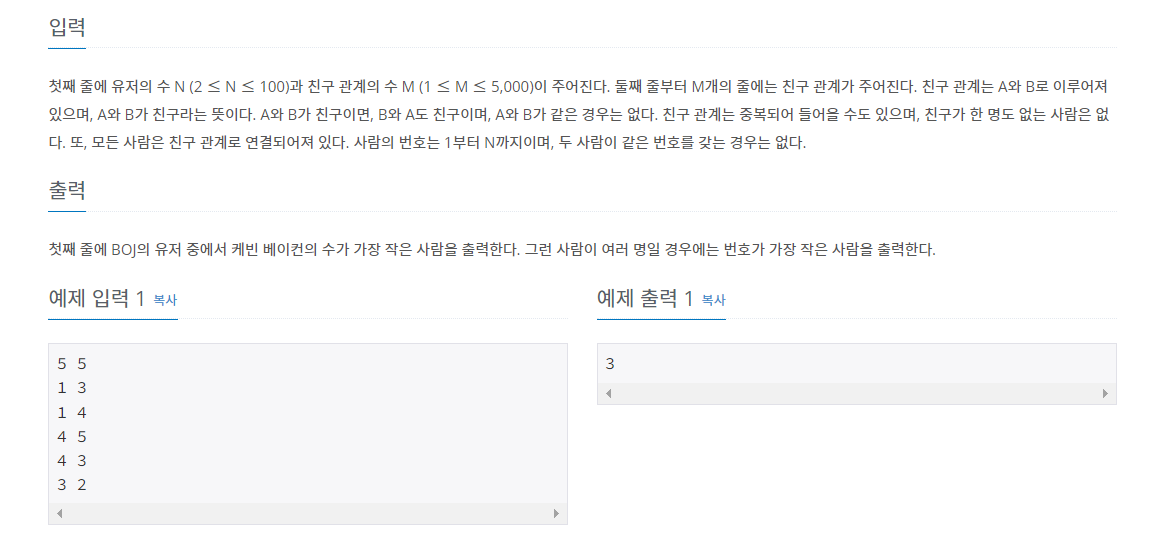
백준

1. Python
import sys
from collections import deque
input = sys.stdin.readline
n, m = map(int, input().split())
relation = [[] for _ in range(n + 1)]
for _ in range(m):
a, b = map(int, input().split())
relation[a].append(b)
relation[b].append(a)
def bfs(start):
count = [0] * (n + 1)
visit[start] = 1
q = deque()
q.append(start)
while q:
x = q.popleft()
visit[x] = 1
for i in relation[x]:
if not visit[i]:
count[i] = count[x] + 1
q.append(i)
visit[i] = 1
return sum(count)
result = []
for i in range(1, n + 1):
visit = [0] * (n + 1)
result.append(bfs(i))
print(result.index(min(result)) + 1)
2. C++
#include <iostream>
#include <vector>
#include <queue>
#include <algorithm>
using namespace std;
int bfs(vector<vector<int>> &relation, int start, int n) {
vector<int> temp(n+1,-1);
queue<int> q;
q.push(start);
temp[start] = 0;
while (!q.empty()) {
int now = q.front(); q.pop();
for (int i = 0; i < relation[now].size(); i++) {
int next = relation[cur][i];
if (temp[next] != -1) continue;
temp[next] = temp[now] + 1;
q.push(next);
}
}
int sum = 0;
for (int i = 1; i <= n;i++) {
sum += dist[i];
}
return sum;
}
int main() {
int n, m;
cin >> n >> m;
vector<vector<int>> relation(n+1);
vector<int> count(n+1);
for (int i = 0; i < m; i++) {
int a, b;
cin >> a >> b;
relation[a].push_back(b);
relation[b].push_back(a);
}
int min_count = 987654321;
int ans = 0;
for (int i = 1; i <= n; i++) {
count[i] = bfs(relation, i, n);
if (count[i] < min_count) {
min_count = count[i];
ans = i;
}
}
cout << ans;
return 0;
}


