리벤 슈테인 알고리즘
-
러시아 과학자 블라디미르 리벤슈테인(Vladimir Levenshtein)가 고안한 알고리즘입니다. 편집 거리(Edit Distance) 라는 이름으로도 불립니다.
-
Levenshtein Distance는 두 개의 문자열 A, B가 주어졌을 때 두 문자열이 얼마나 유사한 지를 알아낼 수 있는 알고리즘입니다.
-
그러니까, 문자열 A가 문자열 B와 같아지기 위해서는 몇 번의 연산을 진행해야 하는 지 계산할 수 있습니다.
-
여기서의 연산이란, 삽입(Insertion), 삽입(Deletion), 대체(Replacement)를 말합니다.
-
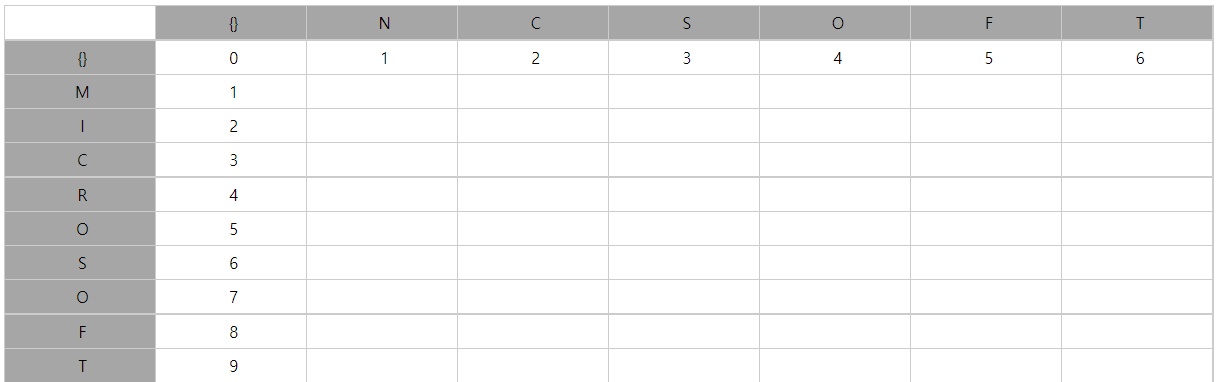
<MICROSOFT & NCSOFT 비교>
-
M과 N을 비교해보자. 이 둘은 다르다. 따라서 값을 변경해야 한다. 코스트는 1이다.
-
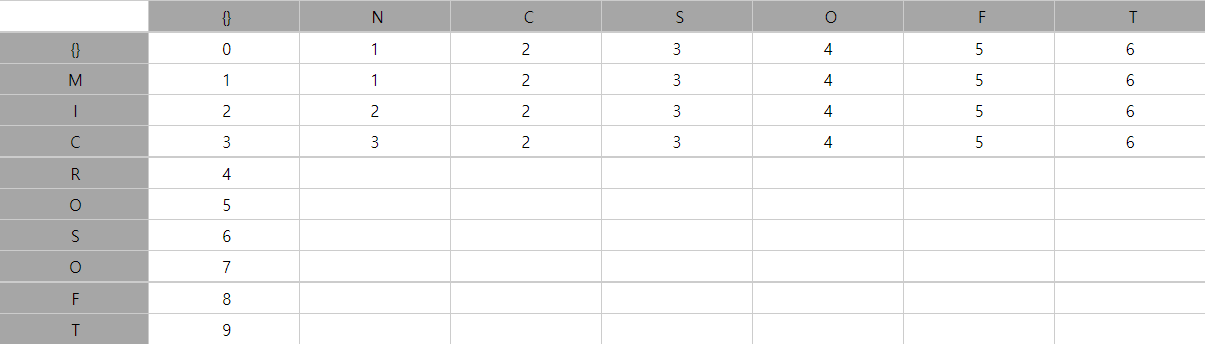
M과 NC이다. 둘 다 다르고, 하나를 지우고 하나를 바꿔야한다. 따라서 코스트는 2이다.
-
M과 NCS를 비교하자. 셋 다 다르고 두개를 지우고 하나를 바꿔야한다. 따라서 코스트는 3이다.
-
여기서 첫 번째, 두 변수가 일치했을 경우 이전의 편집거리를 가져오면 된다고 했다.
- 따라서
A[i] == B[j]일때의 편집거리D(i,j) = D(i-1,j-1)이다.
- 따라서

-
그리고 두 문자가 다를 경우, 이전의 편집 거리에서 1을 증가시켜야 한다고 했다.
-
MI와NCS를 비교한다고 해보자. (위 테이블에서 이 경우 비교하는 대상은I와S이다. 이를 기억하고 보자.) -
왼쪽 대각선 위에 있는건
M와NC를 비교하는 편집거리이다. 위는M과NCS를 비교하는 편집 거리이며, 왼쪽은MI와NC를 비교하는 편집 거리이다.1) 여기서 대각선 M과 NC의 편집거리를 가져오는 것은 I와 S를 같은 문자로, 두 문자열이 같다고 보는 것이다.
- 즉 I를 S로 바꾸면 비교하는 문자가 같으니 M과 NC를 비교한 편집거리를 그대로 가져오고, I를 S로 바꾼 수정을 위한 코스트를 더하는 것이다. (위에서 같을 경우엔 대각선위에 있는 값을 그대로 가져왔었던걸 떠올리면 된다.)
2) 위쪽인 M과 NCS의 편집거리에서 1을 증가시켜 MI,NCS 편집거리에 넣는다는 것은 I를 삭제한다는 것을 뜻한다.
- 즉 M과 NCS의 편집거리를 그대로 가져오고 I를 삭제한 코스트를 추가한다는 뜻이다.
-
-
A[i] != B[j]면,1,2,3번, 각 수정,삽입,삭제를 한 편집거리 중 최소값을 가져오면 된다.- 즉
D(i,j) = min(D(i-1,j)+1,D(i,j-1)+1,D(i-1,j-1)+1)이다.
- 즉
-
정리하면 다음과 같다.
1) 비교하고자 하는 문자 A[i]와 B[j]가 같으면,
D(i,j) = D(i-1,j-1)이다.2) 비교하고자 하는 문자 A[i]와 B[j]가 다르면,
D(i,j) = min(D(i-1,j)+1,D(i,j-1)+1,D(i-1,j-1)+1)이다.
def edit_dist(str1, str2):
n = len(str1)
m = len(str2)
dp = [[0] * (m + 1) for _ in range(n + 1)]
for i in range(1, n + 1):
dp[i][0] = i #첫행 초기화
for j in range(1, m + 1):
dp[0][j] = j #첫열 초기화
for i in range(1, n + 1):
for j in range(1, m + 1):
#문자가 같다면 왼쪽 위에 해당하는 수를 그대로 대입
if str1[i - 1] == str2[j - 1]:
dp[i][j] = dp[i - 1][j - 1]
#문자가 다르다면, 3가지 경우 중에서 최솟값 찾기
else: #삽입(왼쪽), 삭제(위쪽), 교체 (왼쪽 위) 중에서 최소 비용
dp[i][j] = 1 + min(dp[i][j - 1], dp[i - 1][j], dp[i - 1][j - 1])
return dp[n][m]
str1 = input()
str2 = input()
print(edit_dist(str1, str2))
