
4-2. 분포 요약하기
핵심 키워드
matplotlib 산점도 히스토그램 도수 로그 스케일 상자 수염 그래프
산점도
산점도는 두 변수 또는 두 가지 특성값을 직교좌표계에 점으로 나타내는 그래프이다.
파이썬에서 그래프를 그리는 데 사용하는 패키지는 맷플롭립(matplotlib)이다. 그래프 함수를 그리기 위해서는 matplotlib.pyplot 패키지를 불러온다.
scatter(x축좌표, y축좌표) 함수로 산점도를 그린 후 show() 함수로 그래프를 출력한다.
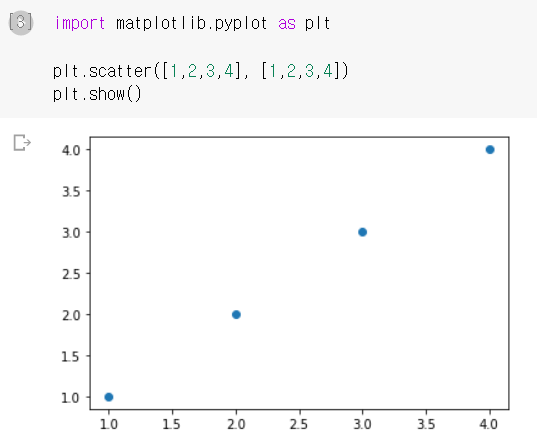
중첩된 데이터를 파악하기 위해서는 alpha 매개변수에 0~1 사이의 값을 넣어 투명도를 조절한다.
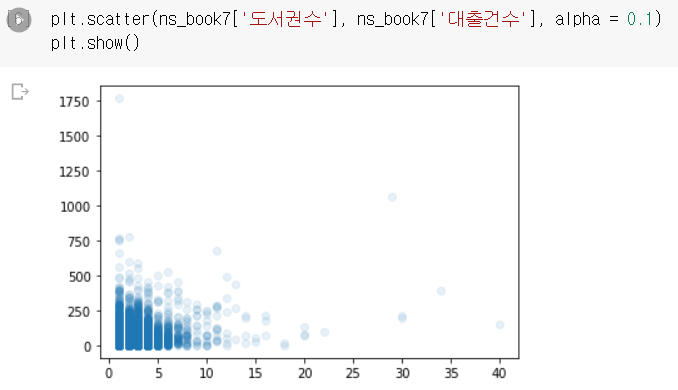
왼쪽 아래에 중첩된 데이터가 많다. 이것의 의미는 대부분의 도서권수가 적다는 것을 의미한다.
도서권수가 대부분 작은 값이기 때문에 도서권수와 대출건수 사이의 관계를 명확히 파악하기 위해 도서권수 열 대신 '대출건수 열을 도서권수 열로 나눈 값'을 사용해보자.
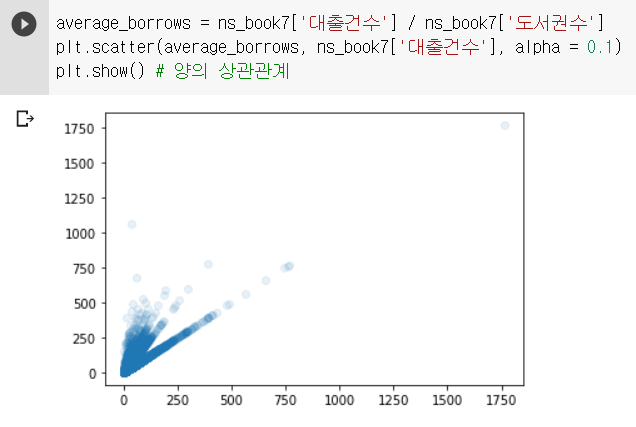
위의 그래프에서 도서권수 당 대출건수가 증가할 수록 도서권수도 증가한다는 것을 알 수 있다.
이처럼 x축이 증가함에 따라 y축이 증가한다면 양의 상관관계가 있다고 말한다.
반대로 x축이 증가함에 따라 y축이 감소한다면 음의 상관관계가 있다는 것이다.
산점도는 2차원 좌표에 데이터를 점으로 나타내기 때문에 두 특성간의 관계를 한 눈에 파악할 수 있다.
하지만 산점도는 2차원 또는 3차원만 가능하기 때문에 한 번에 표현할 수 있는 특성 개수에는 한계가 있다.
히스토그램
반면 히스토그램은 한 가지 특성의 데이터 분포를 확인할 수 있다.
수치형 특성의 값을 일정한 구간(bin 또는 level)으로 나눠 구간 안에 포함된 데이터 개수를 막대 그래프로 그린 것이다.
구간 안에 속한 데이터의 개수를 도수(frequency)라고 한다.
맷플롯립으로 히스토그램을 그릴 때는 hist() 함수를 사용한다.
1차원 데이터를 입력받아서 그래프를 그리고, bins 매개변수로 구간을 지정한다.
예를 들어 아래의 그래프는 5개의 구간으로 나누어진 히스토그램이다. 첫 번째 구간의 도수는 1이고, 두 번째 구간의 도수는 2이다. 최댓값과 최솟값도 각각 13과 0이라는 것을 알 수 있다.
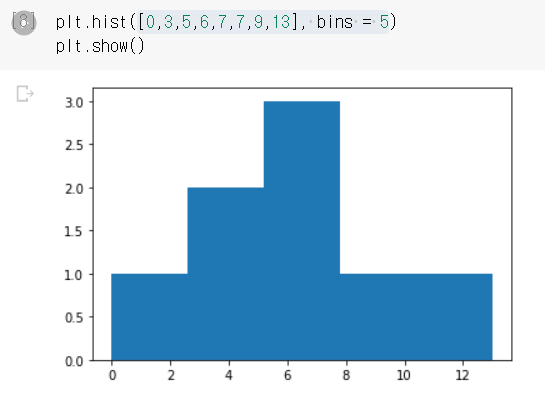
어느 구간의 데이터가 많은지 한 눈에 잘보이지만, 구간이 어떻게 나누어졌는지 수치는 확인할 수 없다.
히스토그램의 구간을 정확히 확인하려면 넘파이의 histogram_bin_edges() 함수를 사용한다.

첫 번째 구간은 0~2.6, 두 번째 구간은 2.6~5.2, 세 번째 구간은 5.2~7.8, 네 번째 구간은 7.8~10.4, 마지막 다섯 번째 구간은 10.4~13이라는 것을 알 수 있다.
이제 더 많은 데이터를 가상으로 만들어 히스토그램을 그려보자.
넘파이의 randn(원하는 샘플 개수) 함수는 표준정규분포를 따르는 랜덤한 실수를 생성한다.
seed() 함수는 유사난수를 생성한다.
randn() 함수는 실행될 때마다 다른 값이 나오는데, 여기서는 책과 실습 결과를 같게 만들기 위해 책에 나와있는 동일한 시드값을 주었다.
랜덤한 값을 생성하는 randn() 함수 전에 seed() 함수를 사용하면 항상 같은 난수를 사용할 수 있다.
random_samples 배열이 표준정규분포를 따르는지 확인하기 위해 평균과 표준편차를 계산해보자.

평균은 약 0.02, 표준편차는 약 0.98이므로 각각 0과 1에 가깝다. 표준정규분포를 따르고 있다고 볼 수 있다.
또한 히스토그램을 그려보면 random_samples가 평균 0 을 중심으로 정규분포 모양이 그려지는 것을 알 수 있다.
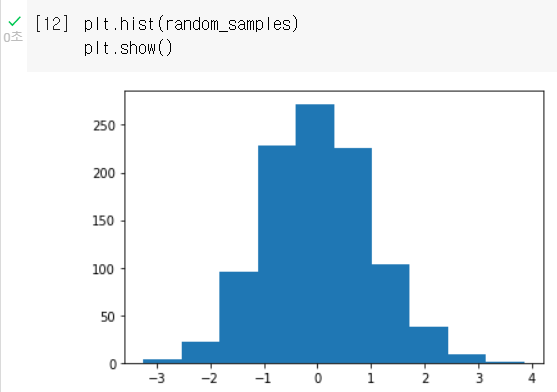
이제 도서관 대출 데이터에서 수치 데이터의 분포를 확인해보자.
대출건수 열의 히스토그램을 아래처럼 그릴 수 있다.
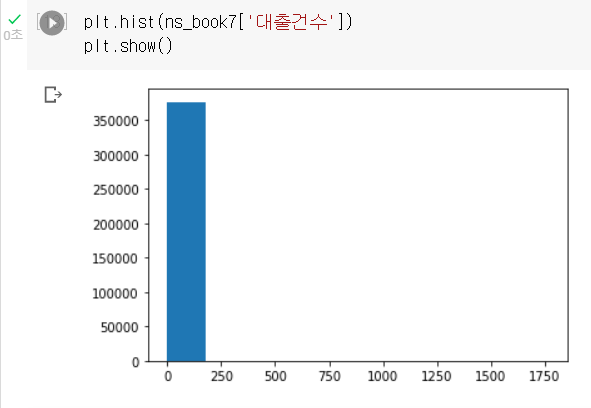
첫 번째 구간을 제외한 다른 구간에는 도수 값이 표시되지 않았다. 산점도에서 확인했듯이 대부분의 대출건수는 앞에 몰려있기 때문이다.
이처럼 한 구간의 도수가 너무 커서 다른 구간에는 도수가 표시되지 않을 때에는 y축을 로그 스케일로 바꿔 해결할 수 있다.
y축에 로그함수를 적용하면 값이 클 수록 도수 크기를 많이 줄일 수 있다.
맷플롯립에서 yscale() 함수에 'log'를 지정하면 된다. (default: 밑이 10인 로그)
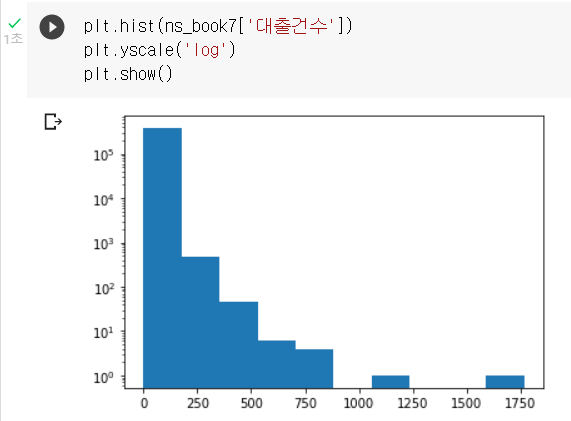
각 구간의 도수는 지수 부분을 고려해서 읽는다. 예를 들어 첫 번째 구간의 도수는 약 370000이다.
로그 스케일로 변환된 그래프를 볼 때보다 실제 데이터는 훨씬 더 격차가 크다.
bins 매개변수의 값을 100으로 바꾸면 데이터의 분포를 좀 더 세밀하게 확인할 수 있다.
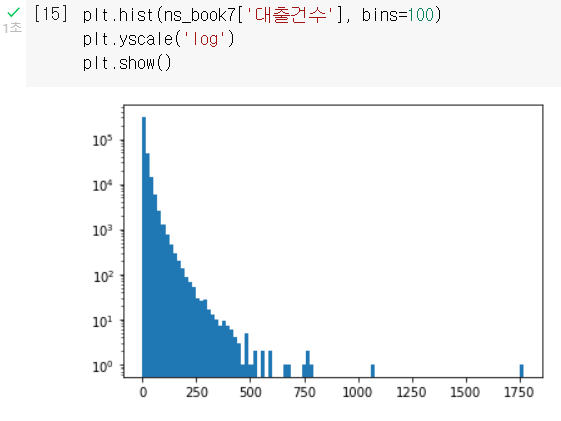
대출건수가 0인 것이 가장 많고, 대출건수가 증가함에 따라 도수가 증가한다는 것을 알 수 있다.
x축에 로그 스케일을 적용하려면 xscale() 함수를 사용한다.
예를 들어 도서명의 길이에 대한 히스토그램을 그리면 아래처럼 데이터가 앞쪽에 몰려있다는 것을 알 수 있다.
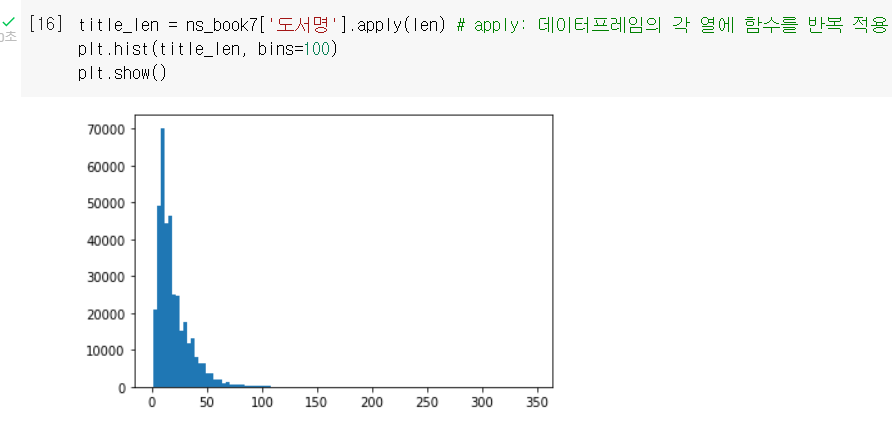
여기서 x축에 로그 스케일을 적용하면 x축을 따라 작은 값과 큰 값의 차이가 줄어든다.
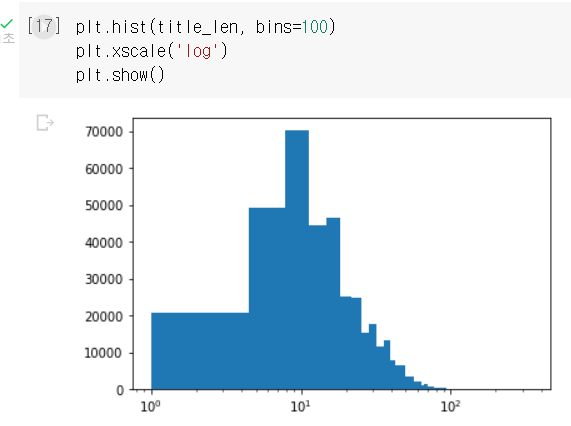
상자 수염 그림
상자 수염 그림은 여러 특성의 분포를 비교할 때 효과적이다.
최솟값, 세 개의 사분위수, 최댓값 5개의 숫자를 사용해 데이터를 요약하는 그래프를 그린다.
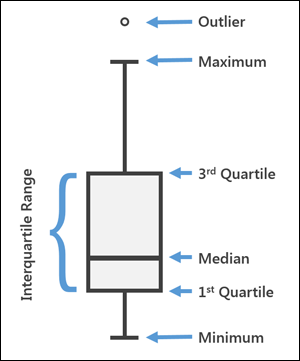
- 제1 사분위수(25%)와 제3 사분위수(75%): 직사각형의 밑면과 윗면
- 중간값(50%): 직사각형 안에 있는 수평선
- 최댓값과 최솟값: 직사각형에서 가장 멀리 있는 샘플까지의 수직선 (수염 길이)
- 이상치: 수직선 밖 영역의 데이터
제1 사분위수와 제3 사분위수 사이의 거리를 IQR(InterQuartile Range)이라고 한다.
상자 수염 그림은 데이터가 어떤 방향으로 더 많이 늘어져 있는지 한 눈에 파악하기 쉽다.
맷플롯립에서는 boxplot() 함수로 그린다.
상자 수염 그림을 수평으로 그려야 할 때는 boxplot() 함수의 vert 매개변수를 기본값 True에서 False로 바꾼다.
xy축이 바뀌기 때문에 로그 스케일도 반전시켜야 한다.
기본적으로 수염 길이는 IQR의 1.5배이다. 이 길이를 조정하려면 boxplot() 함수의 whis 매개변수를 조정한다.
기본값 1.5를 10으로 바꾸면 IQR의 10배 범위 안에서 가장 멀리 떨어진 데이터까지 수염이 그려진다.
whis 매개변수는 백분율로도 지정할 수 있다.
예를 들어 (0,100)으로 지정하면 0%과 100% 백분위수(처음부터 마지막)에 해당하는 데이터까지의 수염을 그린다.

더 알아보기
정규분포와 표준정규분포
- 정규분포(normal distribution): 가운데가 볼록하고 평균을 중심으로 대칭인 분포
- 표준정규분포(standard normal distribution): 평균이 0이고 표준편차가 1인 정규분포

판다스의 그래프 함수
판다스 데이터프레임에서도 여러 가지 그래프를 그릴 수 있는 메서드를 제공한다.
1. 산점도 그리기
판다스 데이터프레임 객체의plot 속성은 여러 가지 그래프를 그릴 수 있는 메소드를 제공한다.
산점도는 scatter() 메서드로 그릴 수 있다. 맷플롯립과는 달리 데이터프레임으로 그래프를 그릴 때는 x축과 y축에 해당하는 열 이름만 지정하면 된다.
ns_book7.plot.scatter('도서권수','대출건수',alpha=0.1)
plt.show()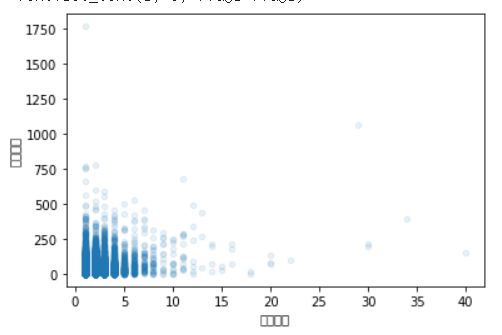
2. 히스토그램 그리기
히스토그램은 hist() 메서드로 그릴 수 있다.
맷플롯립과는 달리 판다스는 데이터프레임에 apply() 메서드를 적용하고 나서 바로 plot.hist() 메서드를 호출할 수 있어 편리하다.
ns_book7['도서명'].apply(len).plot.hist(bins=100)
plt.show() 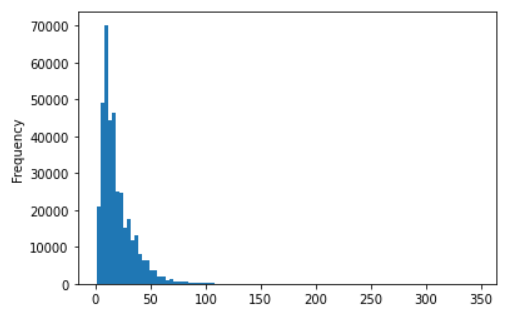
3. 상자 수염 그림 그리기
상자 수염 그림은 boxplot() 메서드로 그린다.
ns_book7[['대출건수','도서권수']].boxplot()
plt.yscale('log')
plt.show() 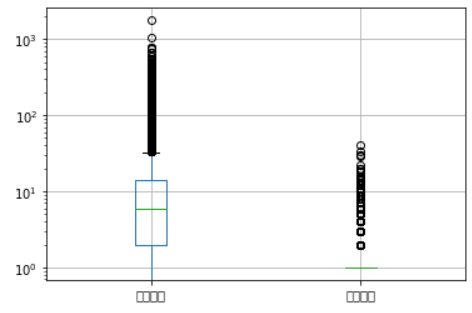
이 메서드들은 열 이름이 한글일 때 그래프의 x축과 y축 이름이 제대로 출력되지 않는다. 이를 해결하려면 코랩에서 따로 한글 폰트를 사용하도록 지정해야 한다. 이러한 그래프 설정 부분은 6장에서 알아보도록 하자.