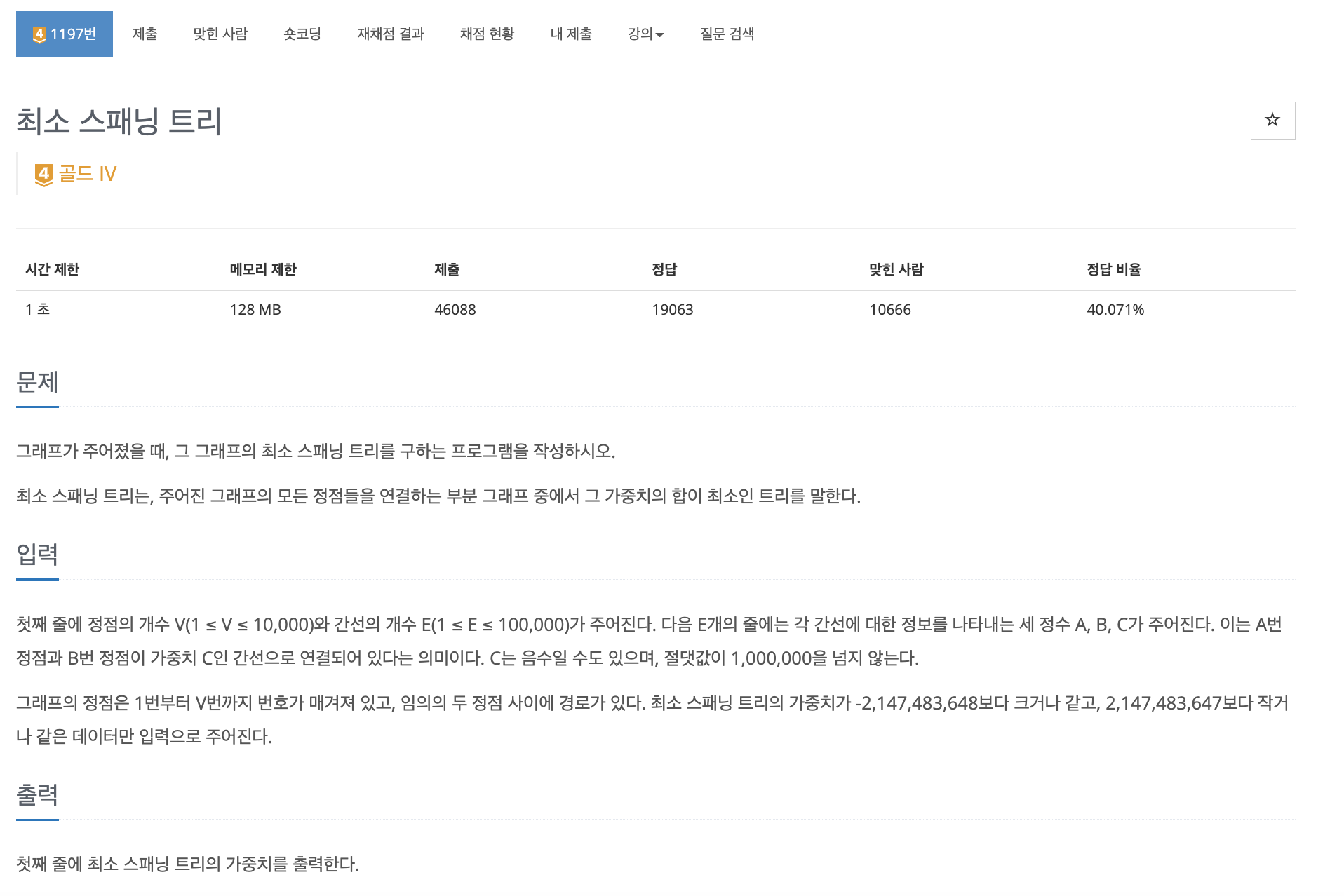
문제
풀이
최소 스패닝(신장) 트리 문제이다.- pypy로 제출하면 메모리 초과가 날 가능성이 높으니 python이 더 유리하다
코드
import sys
input = sys.stdin.readline
sys.setrecursionlimit(100000)
def find_parent(parent: list, x: int) -> int:
if parent[x] == x:
return x
parent[x] = find_parent(parent, parent[x])
return parent[x]
def union_parent(parent: list, a: int, b: int):
a = find_parent(parent, a)
b = find_parent(parent, b)
if a < b:
parent[b] = a
else:
parent[a] = b
def solve() -> int:
result = 0
for edge in edges:
c, a, b = edge
if find_parent(parent, a) != find_parent(parent, b):
union_parent(parent, a, b)
result += c
return result
if __name__ == '__main__':
v, e = map(int, input().split())
parent = [x for x in range(v+1)]
edges = []
for _ in range(e):
a, b, c = map(int, input().split())
edges.append([c, a, b])
edges.sort()
print(solve())
결과

출처 & 깃허브
BOJ 1197
GITHUB


