BOJ/백준-9020-python

문제📖

풀이🙏

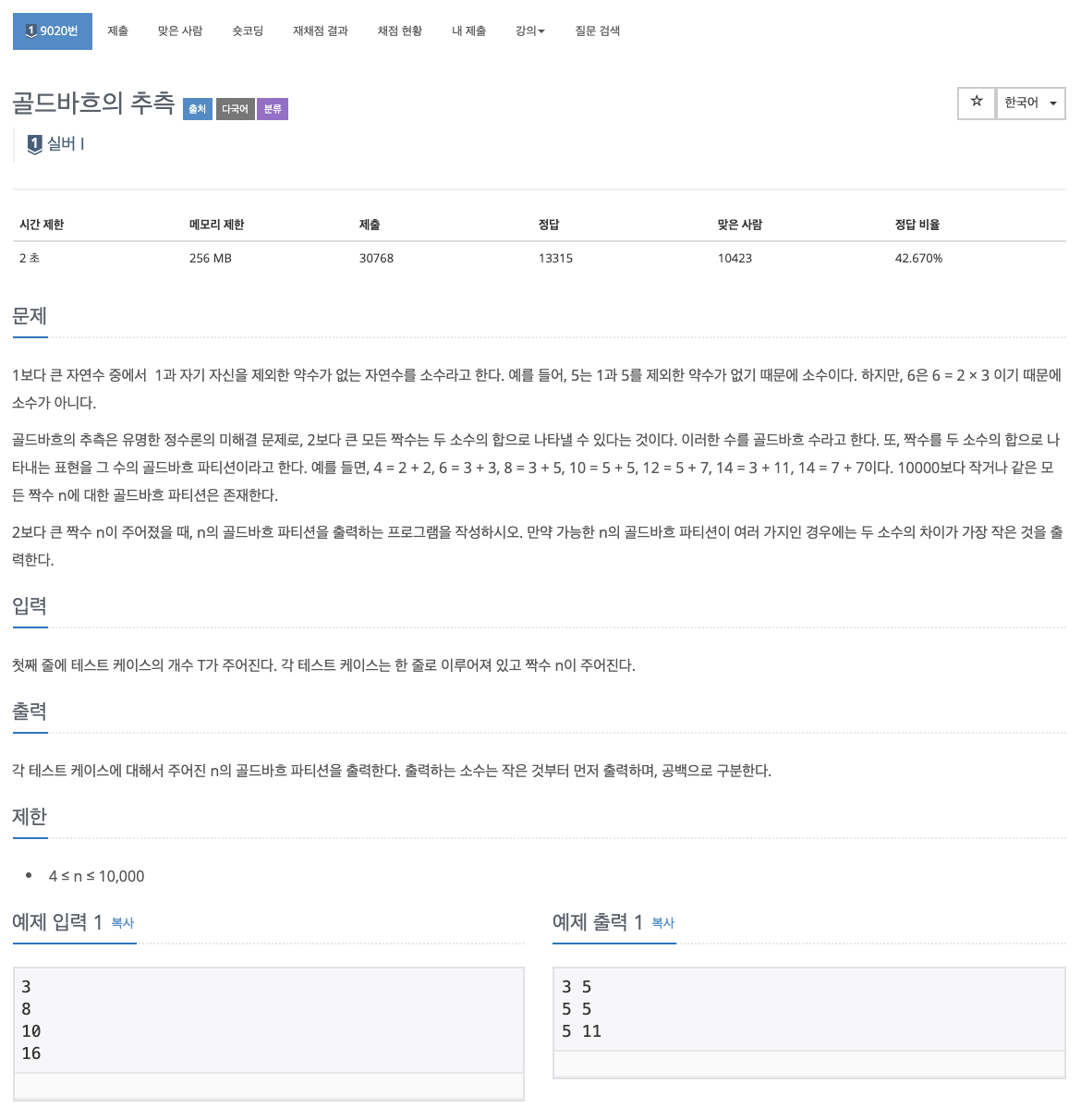
• 첫째 줄에 테스트 케이스의 개수 T가 주어진다.
• 각 테스트 케이스는 한 줄로 이루어져 있고 짝수 n이 주어진다.
• 골드바흐 수란 2보다 큰 모든 짝수는 두 소수의 합으로 나타낼 수 있다는 추측이다.
• 각 테스트 케이스에 대해서 주어진 n의 골드바흐 파티션을 출력한다.
• 출력하는 소수는 작은 것부터 먼저 출력하며, 공백으로 구분한다.
  -> 에라토스테네스의 체 이론 + 골드바흐의 추측 이론 문제이다.

코드💻

# boj, 수학 : 9020, python3
import sys

def prime_list(n):
    sieve = [True] * n
    m = int(n ** 0.5)
    for i in range(2, m + 1):
        if sieve[i] == True:
            for j in range(i+i, n, i):
                sieve[j] = False
    return sieve
 
def gold(primes,n):
    index = 0
    while True:
        if primes[n//2-index] and primes[n//2+index]:
            return(n//2-index,n//2+index)
        index+=1

primes = prime_list(10001)

for _ in range(int(sys.stdin.readline())):
    n = int(sys.stdin.readline())
    answer = gold(primes,n)
    print(answer[0],answer[1])
 

결과😎

출처 && 깃허브📝

https://www.acmicpc.net/problem/9020
github