문제
풀이
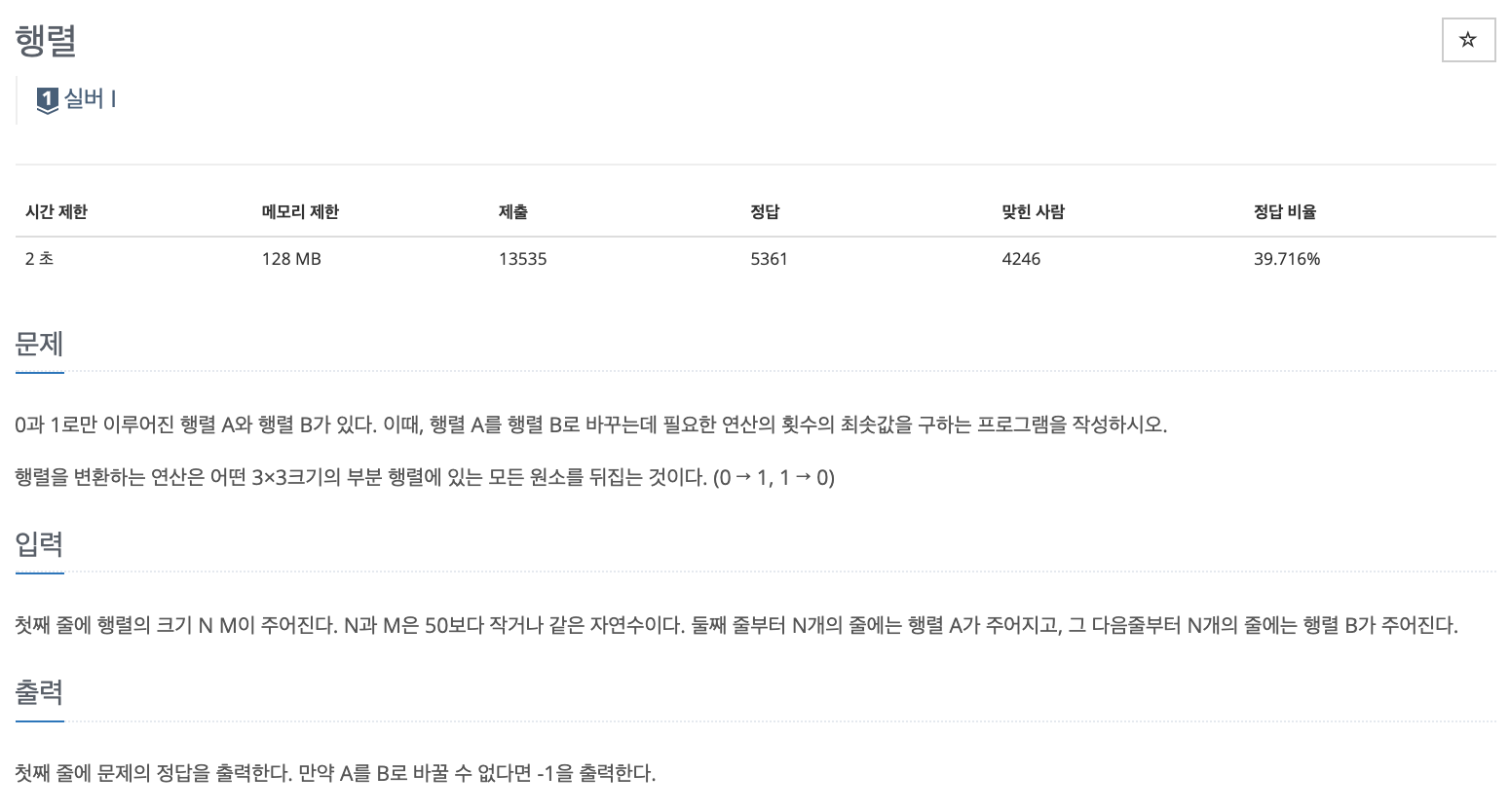
- 시간 제한: 2초
- 0과 1로만 이루어진 행렬 a와 행렬 b가 있다.
- 행렬 a를 행렬 b로 바꾸는데 필요한 연산의 횟수와 최솟값을 구하는 프로그램을 작성하라.
- 첫째 줄에 행렬의 크기 n m이 주어진다.
- n과 m은 50보다 작거나 같은 자연수이다.
- 둘째 줄부터 n개의 줄에는 행렬 a가 주어지고, 그 다음줄부터 n개의 줄에는 행렬 b가 주어진다.
- 첫째 줄에 문제의 정답을 출력한다.
- 만약 a를 b로 바꿀 수 없다면 -1을 출력한다.
-> 이 문제는 말이 행렬이지 실상은 a와 b가 같아질때까지 3x3 구간을 반전시키는 문제로 3x3 오델로 구현 문제이다.
-> (3x3->1), (3x4->2), (3x5->3), (4x4->4), (5x5->9), (4x4->16)로 실행 횟수가 되는걸로보아 (n -2) * (m - 2) 패턴을 가진걸 확인할 수 있다.
-> 본인은 행렬 반전을 할 줄 몰라 (조건문 + 변수 값 할당)으로 구현하였으나 인터넷에 찾아보니 행렬 = 1 - 행렬을 하면 값 반전이 되는걸로 보인다.
코드
import sys
input = sys.stdin.readline
def othello(matrix, x, y):
for i in range(3):
for j in range(3):
if matrix[x+i][y+j] == '0':
matrix[x+i][y+j] = '1'
else:
matrix[x+i][y+j] = '0'
def solve(n, m, matrix_a, matrix_b):
cnt = 0
for x in range(n-2):
for y in range(m-2):
if matrix_a[x][y] != matrix_b[x][y]:
othello(matrix_a, x, y)
cnt += 1
return -1 if matrix_a != matrix_b else cnt
if __name__ == '__main__':
n, m = map(int, input().split())
matrix_a = [list(map(str, input())) for _ in range(n)]
matrix_b = [list(map(str, input())) for _ in range(n)]
print(solve(n, m, matrix_a, matrix_b))
결과

출처 & 깃허브
boj
github


