BOJ 1068/1240) 트리, 노드 사이 거리

트리의 대표유형을 공부한 뒤에 트리 문제를 풀어보았다. 내가 푼 이 두 문제는 트리의 대표유형에 포함될 것 같아서 그 풀이방법을 포스팅해보려 한다.

1. 트리

문제

트리에서 리프 노드란, 자식의 개수가 0인 노드를 말한다.

트리가 주어졌을 때, 노드 하나를 지울 것이다. 그 때, 남은 트리에서 리프 노드의 개수를 구하는 프로그램을 작성하시오. 노드를 지우면 그 노드와 노드의 모든 자손이 트리에서 제거된다.

트리와 삭제할 트리가 주어졌을 때 트리에 남은 리프 노드의 개수를 출력하라.

입력

첫째 줄에 트리의 노드의 개수 N이 주어진다. N은 50보다 작거나 같은 자연수이다. 둘째 줄에는 0번 노드부터 N-1번 노드까지, 각 노드의 부모가 주어진다. 만약 부모가 없다면 (루트) -1이 주어진다. 셋째 줄에는 지울 노드의 번호가 주어진다.

출력

첫째 줄에 입력으로 주어진 트리에서 입력으로 주어진 노드를 지웠을 때, 리프 노드의 개수를 출력한다.

---

풀이과정

이 문제를 보자마자 생각난 것은 순회였다. 트리를 Postorder로 순회하면서 리프노드의 개수를 세고 루트노드까지 반환하며 더해가는 방법이다. 트리의 형태가 결정되어 있을 때 이런 문제는 어떤 순회를 쓰더라도 쉽게 해결될 것으로 보인다. 하지만 문제에서 이 트리의 차수가 정의되지 않았고 루트노드는 -1을 Parent로 갖는다고 나와있을 뿐, 몇 번 노드가 루트라고 정해두지 않았다.

나는 이 문제를 풀 때, 입력과 트리의 표현방법이 익숙치 않아서 조금 시간이 걸렸다.

1. 트리의 표현방법.
   나는 트리 노드가 N-1까지의 음이 아닌 정수임을 이용하여 2차원 리스트를 사용해 트리를 표현하였다.
   i번 노드의 자식들은 트리 리스트의 i번 인덱스의 리스트에 저장된다. 노드들은 모두 정수로 표현되고, 따로 클래스를 정의하진 않았다.

나는 클래스를 정의하는 방식이 이런 문제 풀이를 어렵게 만든다고 판단하였다. 왜냐하면 어떤 문제들의 경우 일단 노드 개수만 주어지고 자식, 부모의 관계는 이후에 정해지는 경우도 있으므로 일단 모든 노드를 객체로 만들고 기억해두는건 구현의 복잡성을 증가시킨다고 생각했기 때문이다. (나중에 한 번 노드로 푸는 것도 시도해봐야겠다.)

2. 트리의 순회방법
   나는 postorder 방식을 이용했다. 이진 트리와 다르게 자식이 여러 개일 경우를 가정했다. 따라서 반복문을 이용해 존재하는 자식 하나당 한 번 씩 재귀적으로 호출하였다.

각 노드의 부모 번호를 입력받는 과정에서 -1이 들어온 순서를 따로 저장하여 root로 만든다. 이후에는 간단하다.

1. 이 노드가 삭제할 노드라면 0을 반환한다.
2. 이 노드가 리프 노드라면 1을 반환한다.
3. 아니라면 각 자식들의 재귀 호출 반환값들을 합하여 반환한다.

마지막으로 root의 결과를 출력하고 실행을 종료한다.

import copy

def getLeafCount(tree, root, R) :
    if root == R : return 0
    leaves = [0] * len(tree[root])
    for i in range(len(leaves)) :
        leaves[i] = getLeafCount(tree, tree[root][i], R)
    
    if not tree[root] or sum(leaves) == 0 : return 1
    return sum(leaves)

def solve() :
    N = int(input())
    tree = [copy.deepcopy([]) for _ in range(N)]
    nodes = list(map(int, input().split()))
    root = 0
    for i, n in enumerate(nodes) :
        if n > -1 : tree[n].append(i)
        else : root = i
    R = int(input())
    
    print(getLeafCount(tree, root, R))

solve()

---

2. 노드 사이의 거리

문제

$N$개의 노드로 이루어진 트리가 주어지고 M개의 두 노드 쌍을 입력받을 때 두 노드 사이의 거리를 출력하라.

입력

첫째 줄에 노드의 개수
$N$과 거리를 알고 싶은 노드 쌍의 개수
$M$이 입력되고 다음
$N-1$개의 줄에 트리 상에 연결된 두 점과 거리를 입력받는다. 그 다음 줄에는 거리를 알고 싶은
$M$개의 노드 쌍이 한 줄에 한 쌍씩 입력된다.

출력

$M$개의 줄에 차례대로 입력받은 두 노드 사이의 거리를 출력한다.

제한사항

$2≤N≤1,000$ 

$1≤M≤1,000$ 
트리 상에 연결된 두 점과 거리는
$10\,000$ 이하인 자연수이다.
트리 노드의 번호는
$1$부터
$N$까지 자연수이며, 두 노드가 같은 번호를 갖는 경우는 없다.

풀이과정

문제의 시간 복잡도를 우선 확인해보자. 노드의 개수가 N개이므로 순회를 사용할 경우 O(N)이고, M번 반복하니 최대 O(M*N)으로 약 10^6의 시간복잡도를 보인다.

이 문제를 최단거리 알고리즘으로 풀 경우 O(N^3) 정도의 시간복잡도를 보이며, 10^9으로 아슬아슬하게 시간제한에 걸릴 가능성이 있다.

당연하게도, 이 문제는 최단거리 알고리즘으로 풀 필요는 없다. 가장 이상적으로 O(N*M)으로 해결이 가능하기 때문이다.

이를 위해 우선 트리에 대해 잠깐 논해보자.

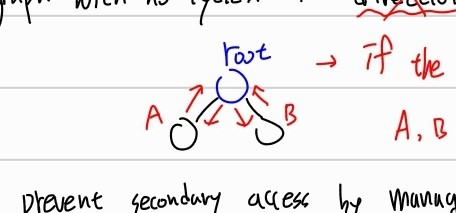
위 사진에서 루트 노드, A 노드, B노드가 있을 때, 우리는 쉽게 root노드가 root 라는 것을 알 수 있다. 이것은 내가 저 트리를 그릴 때 root를 정해뒀기 때문이다.

이제 root라는 단어를 지우고, C노드라고 해보자.

그때도 여전히 C노드가 A노드, B노드의 Parent 인가?
혹자는 그렇다고 말할 수 있으나, 만약 엣지가 양방향으로 연결된다면 이 트리의 루트가 어떤 노드라고 쉽게 말 할 수는 없다.

왜냐하면, A나 B가 루트가 되어도 트리의 정의를 위배하지 않기 때문이다.

즉 필요에 따라서 우리는 트리의 루트 노드를 마음대로 설정할 수 있다. 그럼 트리 자체의 구조가 변화되고 그에 맞춰 최적화된 알고리즘을 적용할 수 있다.

문제로 돌아가서 일단 트리를 2개의 링크로 연결되도록 구성하고, 거리를 알고 싶은 두 노드 A, B를 입력 받는다.

함수를 호출할때, 단지 root 노드로 A나 B중 어느 하나만 주고 순회로 A, B를 찾도록하면 이 문제는 바로 해결된다. 단, 링크가 이중이기 때문에 방문했음을 기록할 자료구조가 추가로 요구된다.

나는 처음에 이 문제를 Lowest Common Anccester 알고리즘으로 해결하려 했지만, 중간에 A나 B 중 어느하나가 다른 하나의 조상 노드인 경우나 다른 여러 상황을 고려하는 것이 번거로워서 다른 방법을 택하게 되었다.

다음은 프로그램 전문이다.

import sys
from copy import deepcopy as dcp

def getShortestDist(tree, root, B, visited) :
    visited.add(root)
    if root == B : return (True, 0)
    for i, n in enumerate(tree[root]) :
        if n[0] not in visited :
            child_flag, child_weight = getShortestDist(tree, n[0], B, visited)
            if child_flag :
                return (True, child_weight + n[1])
    return (False, 0)

def solve():
    N, M = tuple(map(int, input().split()))
    tree = [dcp([]) for _ in range(N + 1)] # 저장 형식은 (노드, 가중치)
    
    for _ in range(N-1) :
        P, C, D = tuple(map(int, input().split()))
        tree[P].append((C,D))
        tree[C].append((P,D))
    
    for _ in range(M) :
        dist= [sys.maxsize]*(N+1)
        A, B = tuple(map(int, input().split()))
        visited = set()
        dist = getShortestDist(tree, A, B, visited=visited)
        print(dist[1])

solve()