문제 링크)
https://www.acmicpc.net/problem/16236
입력
첫째 줄에 공간의 크기 N(2 ≤ N ≤ 20)이 주어진다.
둘째 줄부터 N개의 줄에 공간의 상태가 주어진다. 공간의 상태는 0, 1, 2, 3, 4, 5, 6, 9로 이루어져 있고, 아래와 같은 의미를 가진다.
0: 빈 칸
1, 2, 3, 4, 5, 6: 칸에 있는 물고기의 크기
9: 아기 상어의 위치
아기 상어는 공간에 한 마리 있다.
출력
첫째 줄에 아기 상어가 엄마 상어에게 도움을 요청하지 않고 물고기를 잡아먹을 수 있는 시간을 출력한다.
풀이과정
문제 이해
주어지는 정보는 모두 정수이다. N X N의 정사각 행렬에는 물고기의 크기(1~6), 상어의 위치(9), 빈 공간(0)이 포함되어 있다.
이런 그리드 형태의 자료구조는 implicit graph로 볼 수 있는데, 간선과 노드 정보는 주어지지 않지만, 리스트의 각 공간이 노드이고 이동 방향으로 인접한 공간에 간선이 연결되어 있다고 가정할 수 있다.
그래프의 정의를 다시 되짚어보자면 이런 관점이 합리적이라는 사실을 알 수 있다.
그래프 : Vertex와 Edge의 집합
따라서 Vertex와 Edge(방향성 같은 개념으로) 정의가 가능하다면 그래프로 근사할 수 있지 않을까 생각해보았다.
물고기를 먹을 수록 상어의 몸집이 불어나는 점, 먹을 수 없는 물고기에 둘러싸인 물고기는 먹을 수 없다는 점, 물고기는 거리가 가까운 순으로, 동일 거리이면 가장 위에 있는 것을, 그마저 여러개라면 그 중 왼쪽의 것을 선택한다.
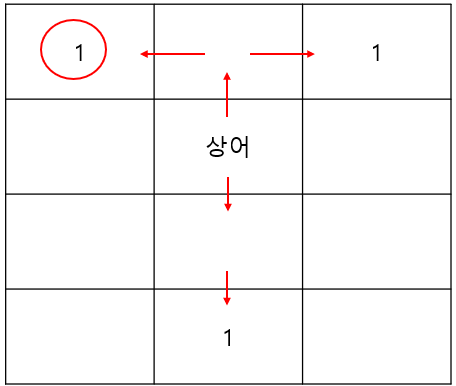
위와 같은 상황에서 상어는 가장 0,0 위치의 물고기를 먹으러 갈 것이다. 그리고 변화된 위치에서 다시 가장 가까운 물고기를 찾는 것을 반복할 것이다.
동일한 거리에 있는 물고기들은 다음과 같은 등고선으로 연결될 수 있다.
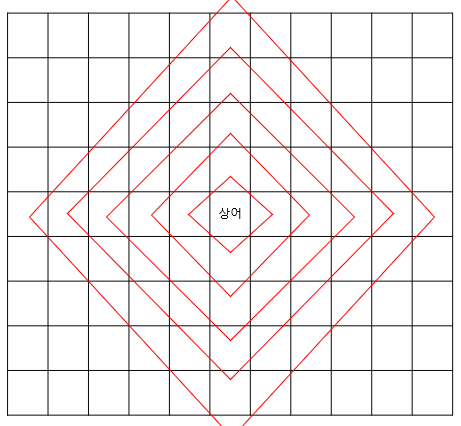
이렇게 보니 BFS를 쓰면 동일한 거리에 있는 공간들을 훑으며 진행하므로 가장 가까운 물고기를 찾는 문제는 가장 먼저 만나는 물고기를 찾는 것으로 해결 할 수 있을 것이다.
전체 노드의 개수는 20 x 20 = 400개로 O(N^2) 시간 복잡도까지 안전하게 적용할 수 있을 것이다.
접근방법
문제에서 구해야하는 것은 상어가 먹을 수 있는 물고기를 모두 먹을 때까지 걸리는 시간을 구하는 것이므로 상어로부터 가장 가까운 물고기들을 먹어가며, 상어의 크기가 변하는 것을 반영해 더이상 먹을 수 있는 물고기가 순회에서 발견되지 않을 때 까지 BFS나 DFS를 적용해 볼 수 있을 것 같다.
문제이해에서 BFS가 적절할 것이라고 생각하였고, 이것을 기반으로 어떻게 문제를 해결할 것인지 생각해야한다.
문제의 조건 중 동일한 거리의 물고기 중에선 가장 위에 있으며 가장 왼쪽에 있는 물고기를 먹으러 간다고 했다. 여러 다른 문제들을 해결하면서 DFS나 BFS가 그리드를 순회할 때 다음과 같은 방식으로 순회를 했다.
BFS의 경우 큐에서 한 노드를 꺼내 가능한 모든 방향의 노드에 방문하고, DFS의 경우 한 노드에서 갈 수 있는 경로의 끝까지 우선 탐색했다.
이런 방식은 이번 문제에서 적절하지 못하게 작용한다. 다음과 같은 경우를 생각해보면 그 이유를 알 수 있다.
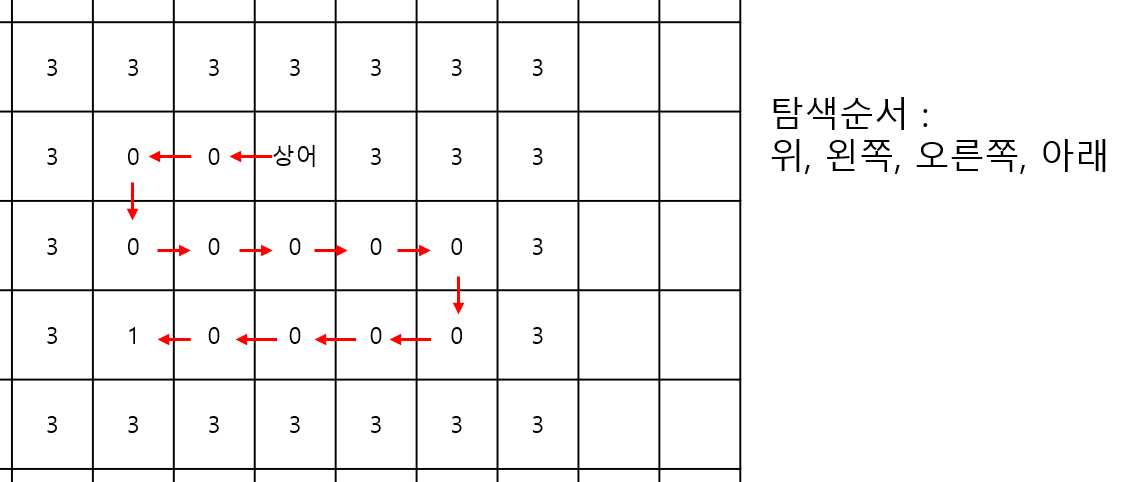
DFS를 사용할 경우 1을 먹기 위해 이동하는 경로가 무려 12가 된다. 물론 좌표를 이용하여 정확한 거리를 계산하는 것이 가능하다.(맨하탄 거리)
하지만 이런 방식은 규칙에 의한 가장 가까우면서 가장 위, 왼쪽의 물고기를 정확히 선택할 수 있을지 불안하다.
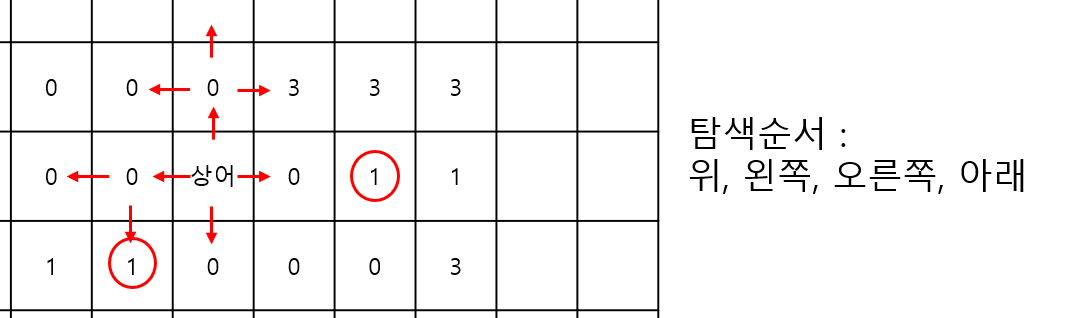
BFS에 오른쪽 탐색 순서를 적용한 결과, 실제로 먹어야 하는 상어 오른쪽의 1이 아니라 상어 왼쪽 아래의 1을 먼저 발견하게 된다.
동일한 거리의 노드들을 정렬하여 탐색할 수도 있겠지만, 정렬 알고리즘에 의해 시간복잡도가 증가할 것이다.
이런 상황을 타개하기 위하여 다음과 같은 방법을 생각해 볼 수 있다.
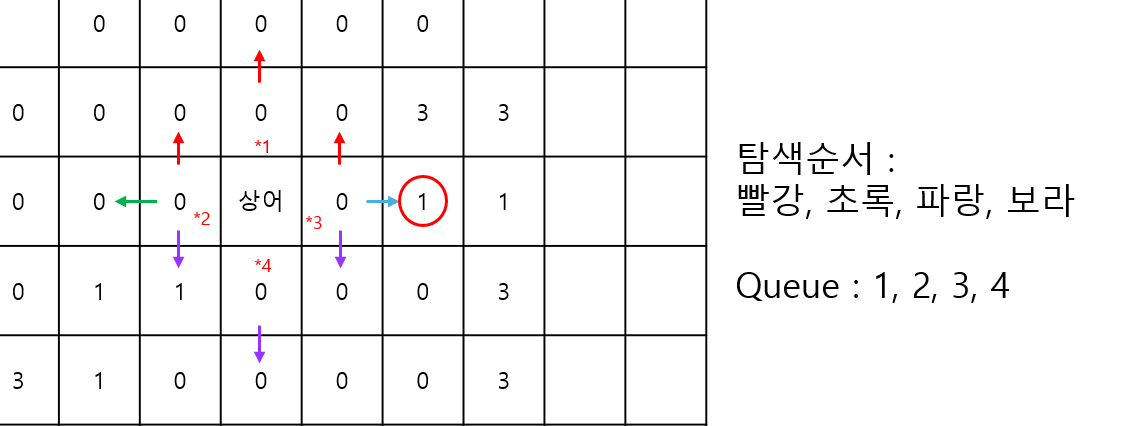
큐에는 1, 2, 3, 4번으로 번호가 부여된 노드들이 들어있고, 이들을 큐에서 꺼내 모든 방향 순회 후 삭제하는 것이 아니라 각 노드에 대해 한 방향씩 적용해보며 탐색하는 방법이다. 재귀적으로 동작하면서 문제에서 조건으로 하는 우선 순위를 적용할 수 있을 것이다.
여기서 또 한가지 주의할 점은 왼쪽, 오른쪽 노드 검사를 한 번에 수행해야 한다는 것이다. 왜냐하면, 큐의 모든 노드에 대해 왼쪽 검사를 수행하다간 위에서 보인 문제가 해결되지 않기 때문이다.
프로그램 코딩
다음은 위 알고리즘을 구현한 프로그램 코드이다.
import sys
from collections import deque
def solve() :
N = int(sys.stdin.readline())
grid = []
for _ in range(N) :
grid.append(list(map(int, sys.stdin.readline().split())))
if 9 in grid[-1] :
shark_row = len(grid) - 1
shark_col = grid[-1].index(9)
steps = (((-1, 0), None), ((0, -1), (0, 1)), ((1, 0), None))
shark_before = (-1, -1)
shark_size = 2
eaten_fishes = 0
passed_time = 0
def BFS(row, col) :
first_queue = deque()
second_queue = deque()
first_queue.append((row, col, 0))
visited = set()
visited.add((row, col))
while first_queue :
for s in steps:
for c in first_queue :
for sb in s :
if sb is None : continue
next_row = c[0] + sb[0]
next_col = c[1] + sb[1]
if 0 <= next_row and next_row < N and 0 <= next_col and next_col < N :
if (next_row, next_col) not in visited :
visited.add((next_row, next_col))
if grid[next_row][next_col] == 0 or grid[next_row][next_col] == shark_size :
second_queue.append((next_row, next_col, c[2] + 1))
elif grid[next_row][next_col] < shark_size :
return (next_row, next_col, c[2] + 1)
first_queue = second_queue
second_queue = deque()
return (row, col, 0)
while shark_before != (shark_row, shark_col) :
shark_before = (shark_row, shark_col)
(shark_row, shark_col, sec) = BFS(row=shark_row, col=shark_col)
passed_time += sec
grid[shark_before[0]][shark_before[1]] = 0
grid[shark_row][shark_col] = 9
if shark_before != (shark_row, shark_col) :
eaten_fishes += 1
if eaten_fishes % shark_size == 0 :
eaten_fishes = 0
shark_size += 1
print(passed_time)
solve()