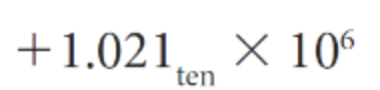Scientific notation
100 = 10^2 = 1 x 10^2
제일 앞글자만 남기고 뒤를 지수로 표현하는 방법으로 normalized 되었다고 말함.
이진수에서는 normalized되기 위해 맨 앞에 1만 올 수 있음
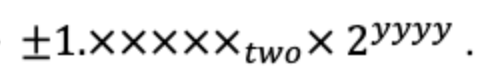
부동소수점 표현 형식

S(1bit) : Sign bit 부호
E(8bit) : Exponent 지수부 - 지수가 음수인 경우도 계산하기 위해 2의 보수로 표현됨
F(23bit) : Fraction 소수부 (0과 1사이)
overflow and underflow
overflow
표현하려는 숫자가 너무 커서 8bit exponent로 다 표현하지 못하는 상황
underflow
표현하려는 숫자가 너무 작아서 (-방향으로 너무 큰 경우) 8bit exponent로 다 표현하지 못하는 상황
-> 64bit double floating-point format을 사용한다
하나의 register를 전부 fraction을 나타내는데에 사용한다

IEEE 745 Floating Point
normalized된 표현에서 맨 앞자리는 항상 1이므로 생략함
-> 유효숫자가 24개가 된다 (fraction 23개 + hidden bit 1개)
F : 1010 이면 실제로는 1.1010 (앞에 1은 Hidden bit로 생략!)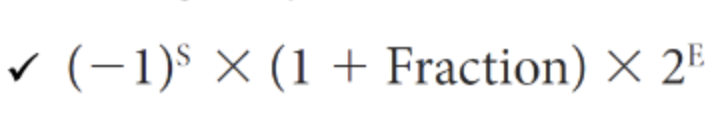
significand
single precision : 24 bit (1 + 23 bits fraction)
double precision : 53 bit (1 + 52 bits fraction)
fraction
single precision : 23 bit
double precision : 52 bit
🚨 Biased Notation
sign bit가 있으므로 1이 많다고 무조건 큰게 아님. 값의 비교가 불가능하므로 값의 비교를 용이하게 하기 위해서 사용 Exponent를 Exponent - Bias로 표현한다.
Bias
single precision : 127
double precision : 1023
✅ single precision
원래 exponent의 범위는 8bit이므로 00000001 ~ 11111111 10진수로 하면 1 ~ 254
근데 비교를 위해서 bias값인 127을 빼서 범위 계산을 해야하므로
Biased Notation을 사용한 exponent의 범위는 -126 ~ 127
✅ special symbol
exponent 0000 0000 은 0으로 예약되어 있다.
exponent 1111 1111 은 무한대, NaN으로 예약되어 있다.
따라서 32bit floating point의 가장 작은 숫자는 Exponenet가 0000 0001 (-126 + 127 = 1)
가장 큰 숫자는 Exponent가 1111 1110 (127 + 127 = 254)
cf) biased notation을 없애고 계산하려면 +127하는 것
Floating Point 덧셈
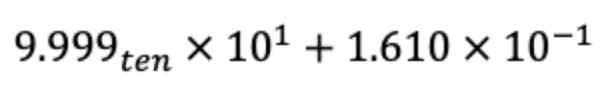
1. 큰 수를 기준으로 exponent 맞춰주기
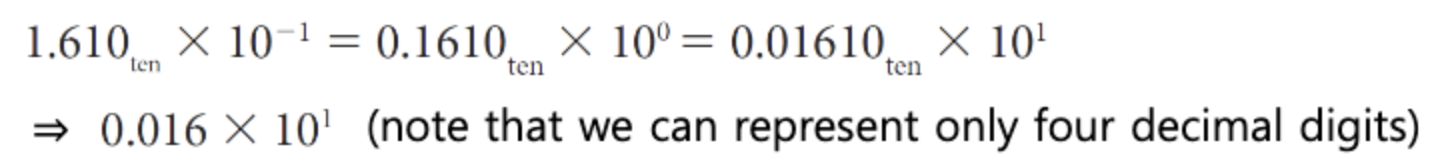
이때 문제에서 significand는 4자리까지만 허용한다고 했으니 significand를 4자리로 맞춰주기
0.01610 => 0.016
2. significand (유효숫자) 더해주기
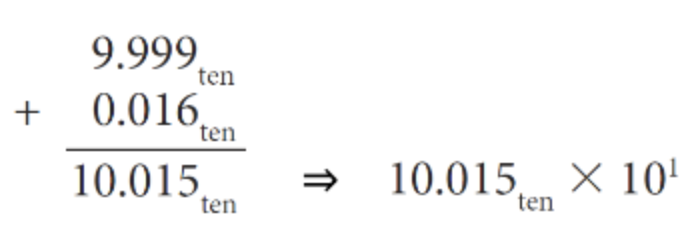
값이 normalized number가 아니므로 normalized number로 맞춰주기
3. normalized number로 맞추기
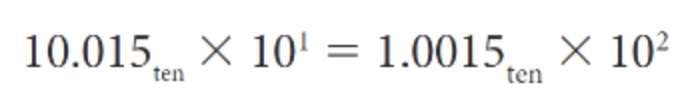
significand가 4개로 제약되어있으니, 반올림을 하여 4자리로 맞춰준다
(참고로 significand가 4자리면 fraction은 4-1=3자리임!)
4. 반올림해서 significand 맞춰주기
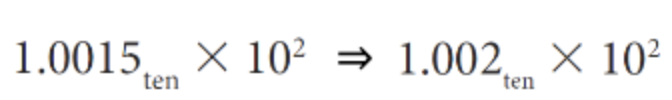
Floating Point 곱셈
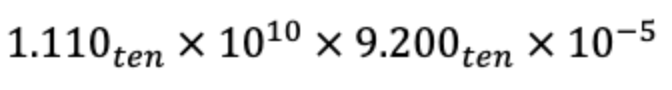
1. biased Exponent 부분 계산하기
그냥 지수부 계산하듯이 계산해도 되지만, biased값을 확인해서 계산하기
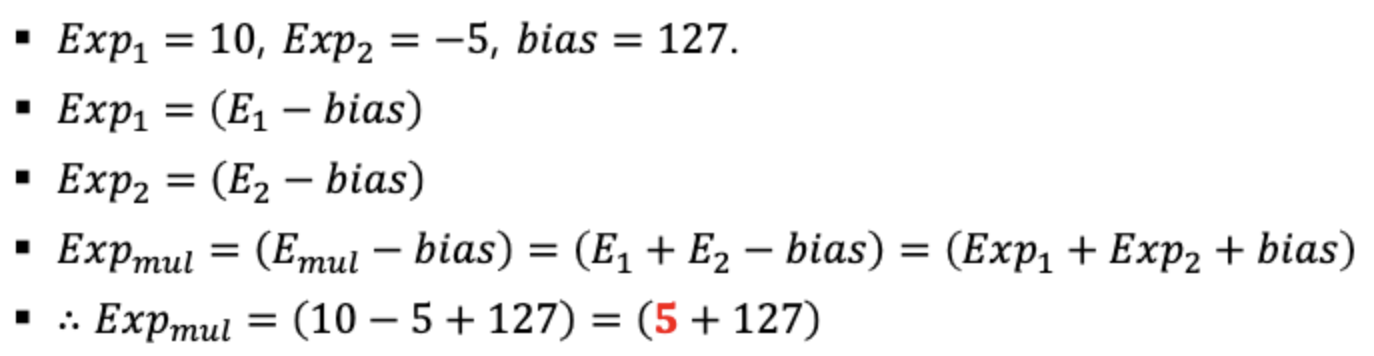
2. significand (유효숫자) 곱셈

3. normalized number로 맞춰주기
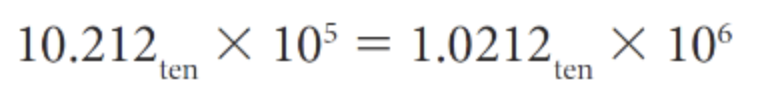
4. significand 조건에 맞게 반올림 해주기
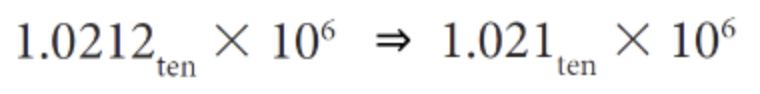
5. 부호 결정!
피연산자들의 부호로부터 결과 부호를 결정한다