dfs를 활용한 최단 경로 구하기, Javascript

문제

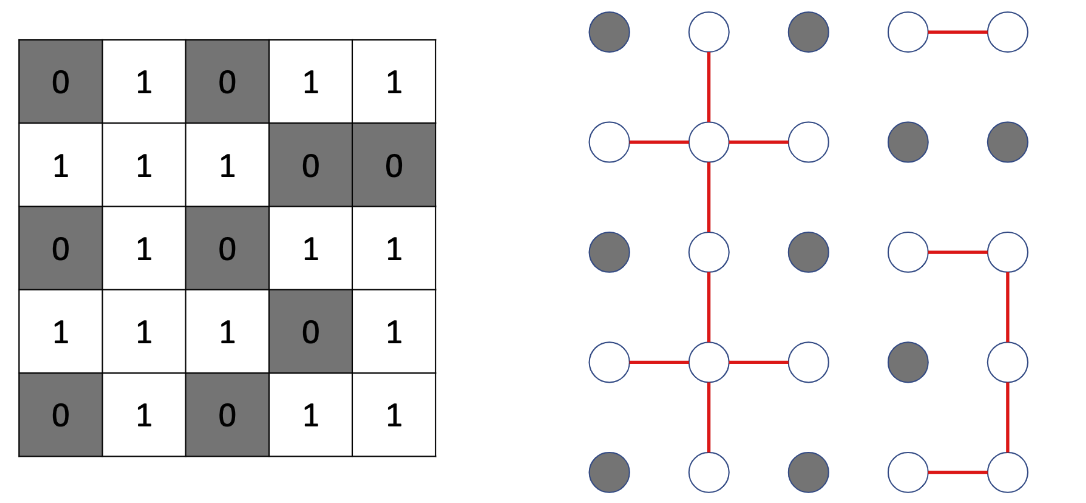
세로와 가로의 길이가 각각 M, N인 방의 지도가 2차원 배열로 주어졌을 때, 1은 장애물을 의미하고 0 이동이 가능한 통로를 의미합니다. 로봇은 지도 위를 일분에 한 칸씩 상하좌우로 이동할 수 있습니다. 로봇의 위치와 목표 지점이 함께 주어질 경우, 로봇이 목표 지점까지 도달하는 데 걸리는 최소 시간을 리턴해야 합니다.

주의 사항

M, N은 20 이하의 자연수입니다.
src, dst는 항상 로봇이 지나갈 수 있는 통로입니다.
src에서 dst로 가는 경로가 항상 존재합니다.

입출력 예시

let room = [
  [0, 0, 0, 0, 0, 0],
  [0, 1, 1, 0, 1, 0],
  [0, 1, 0, 0, 0, 0],
  [0, 0, 1, 1, 1, 0],
  [1, 0, 0, 0, 0, 0],
];
let src = [4, 2];
let dst = [2, 2];
let output = robotPath(room, src, dst);
console.log(output); // --> 8

풀이 코드

const robotPath = function (room, src, dst) {
	const checkRoute = (M, N, current, count) => {
    	const [row, col] = current;
        
        if(row < 0 || col < 0 || row >= M || col >= N) return;
        
        if(room[row][col] === 0 || room[row][col] > count){
        	room[row][col] = count;
        } else {
        	// 1이라는 장애물로 막혀있거나, 최단 거리가 아닌경우 return 한다.
        	return 
        }
        
        checkRoute(M, N, [row + 1, col], count + 1);
        checkRoute(M, N, [row - 1, col], count + 1);
        checkRoute(M, N, [row, col + 1], count + 1);
        checkRoute(M, N, [row, col - 1], count + 1);
    }
    checkRoute(room.length, room[0].length, src, 1);
    const[row, col] = dst;
    return room[row][col] - 1;
};

dfs 문제는 언제 풀어도 어렵다. 기존 상하좌우 구하는 공식을 가져와 풀었습니다.
혼자 풀었다기 보다는 구글 검색을 통해 해결한 문제라 dfs, bfs 관련된 문제를 많이 풀어봐야겠습니다.