[백준] #21608 상어 초등학교(python)

수영·2022년 10월 10일

백준

목록 보기

73/117

📌문제

상어 초등학교에는 교실이 하나 있고, 교실은 N×N 크기의 격자로 나타낼 수 있다. 학교에 다니는 학생의 수는 N2명이다. 오늘은 모든 학생의 자리를 정하는 날이다. 학생은 1번부터 N2번까지 번호가 매겨져 있고, (r, c)는 r행 c열을 의미한다. 교실의 가장 왼쪽 윗 칸은 (1, 1)이고, 가장 오른쪽 아랫 칸은 (N, N)이다.

선생님은 학생의 순서를 정했고, 각 학생이 좋아하는 학생 4명도 모두 조사했다. 이제 다음과 같은 규칙을 이용해 정해진 순서대로 학생의 자리를 정하려고 한다. 한 칸에는 학생 한 명의 자리만 있을 수 있고, |r1 - r2| + |c1 - c2| = 1을 만족하는 두 칸이 (r1, c1)과 (r2, c2)를 인접하다고 한다.

비어있는 칸 중에서 좋아하는 학생이 인접한 칸에 가장 많은 칸으로 자리를 정한다.
1을 만족하는 칸이 여러 개이면, 인접한 칸 중에서 비어있는 칸이 가장 많은 칸으로 자리를 정한다.
2를 만족하는 칸도 여러 개인 경우에는 행의 번호가 가장 작은 칸으로, 그러한 칸도 여러 개이면 열의 번호가 가장 작은 칸으로 자리를 정한다.
예를 들어, N = 3이고, 학생 N2명의 순서와 각 학생이 좋아하는 학생이 다음과 같은 경우를 생각해보자.

학생의 번호	좋아하는 학생의 번호
4	2, 5, 1, 7
3	1, 9, 4, 5
9	8, 1, 2, 3
8	1, 9, 3, 4
7	2, 3, 4, 8
1	9, 2, 5, 7
6	5, 2, 3, 4
5	1, 9, 2, 8
2	9, 3, 1, 4

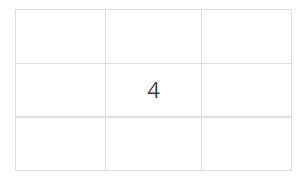
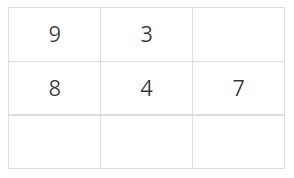
가장 먼저, 4번 학생의 자리를 정해야 한다. 현재 교실의 모든 칸은 빈 칸이다. 2번 조건에 의해 인접한 칸 중에서 비어있는 칸이 가장 많은 칸인 (2, 2)이 4번 학생의 자리가 된다.

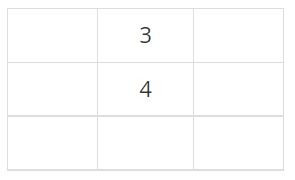
다음 학생은 3번이다. 1번 조건을 만족하는 칸은 (1, 2), (2, 1), (2, 3), (3, 2) 이다. 이 칸은 모두 비어있는 인접한 칸이 2개이다. 따라서, 3번 조건에 의해 (1, 2)가 3번 학생의 자리가 된다.

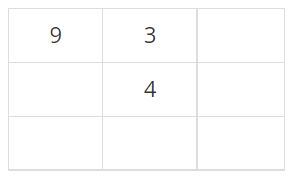
다음은 9번 학생이다. 9번 학생이 좋아하는 학생의 번호는 8, 1, 2, 3이고, 이 중에 3은 자리에 앉아있다. 좋아하는 학생이 가장 많이 인접한 칸은 (1, 1), (1, 3)이다. 두 칸 모두 비어있는 인접한 칸이 1개이고, 행의 번호도 1이다. 따라서, 3번 조건에 의해 (1, 1)이 9번 학생의 자리가 된다.

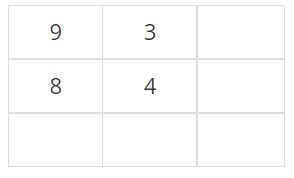
이번에 자리를 정할 학생은 8번 학생이다. (2, 1)이 8번 학생이 좋아하는 학생과 가장 많이 인접한 칸이기 때문에, 여기가 그 학생의 자리이다.

7번 학생의 자리를 정해보자. 1번 조건을 만족하는 칸은 (1, 3), (2, 3), (3, 1), (3, 2)로 총 4개가 있고, 비어있는 칸과 가장 많이 인접한 칸은 (2, 3), (3, 2)이다. 행의 번호가 작은 (2, 3)이 7번 학생의 자리가 된다.

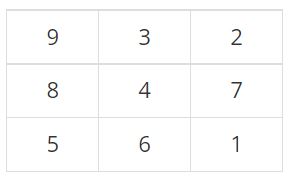
이런식으로 학생의 자리를 모두 정하면 다음과 같다.

이제 학생의 만족도를 구해야 한다. 학생의 만족도는 자리 배치가 모두 끝난 후에 구할 수 있다. 학생의 만족도를 구하려면 그 학생과 인접한 칸에 앉은 좋아하는 학생의 수를 구해야 한다. 그 값이 0이면 학생의 만족도는 0, 1이면 1, 2이면 10, 3이면 100, 4이면 1000이다.

학생의 만족도의 총 합을 구해보자.

입력

첫째 줄에 N이 주어진다. 둘째 줄부터 N2개의 줄에 학생의 번호와 그 학생이 좋아하는 학생 4명의 번호가 한 줄에 하나씩 선생님이 자리를 정할 순서대로 주어진다.

학생의 번호는 중복되지 않으며, 어떤 학생이 좋아하는 학생 4명은 모두 다른 학생으로 이루어져 있다. 입력으로 주어지는 학생의 번호, 좋아하는 학생의 번호는 N2보다 작거나 같은 자연수이다. 어떤 학생이 자기 자신을 좋아하는 경우는 없다.

출력

첫째 줄에 학생의 만족도의 총 합을 출력한다.

제한

3 ≤ N ≤ 20

예제 입력1

예제 출력1

예제 입력2

예제 출력2

백준 21608번 문제

💡Idea

🦈🏫 문제에서 요구하는 바를 열심히 구현하여 해결한 문제입니다🤗

저는 아래와 같이 단계에 따라 구현하여 문제를 풀었습니다.

각 학생들이 좋아하는 학생들과 인접해 있는 칸을 탐색하여 자리 후보로 추가한다.

만약 좋아하는 학생들이 모두 아직 자리가 정해지지 않았다면, 그냥 남아있는 빈 칸들을 모두 후보로 한다.

어떻게 좋아하는 학생들이 가장 많이 인접해 있는 자리를 찾을 수 있을까에 대해서 많은 고민을 해보았습니다.

저는 좋아하는 학생들과 인접하고 비어있는 자리의 좌표를 전부 다 찾고, 가장 많이 중복되는 좌표를 가장 많은 좋아하는 학생들과 인접한 자리로 구현하였습니다.

따라서, 첫 번째 단계에서는 좋아하는 학생들과 인접하고 비어있는 자리의 좌표를 모두 찾아 줍니다.

후보 자리들에 대하여 아래의 순서대로 정렬한다.
1) 좋아하는 학생들과 가장 많이 인접해있는 순서
2) 주변에 앉을 수 있는 빈 자리가 가장 많은 순서
3) 자리 좌표의 행 순서
4) 자리 좌표의 열 순서

1)의 순서 조건은 1번과 연결되는 이야기입니다.

가장 많이 중복되는 좌표의 자리가 좋아하는 학생들과 가장 많이 인접해있는 자리이기 때문에 1에서 구한 후보들을 중복되는 개수 순으로 정렬합니다.

2), 3), 4)의 경우 문제에 나와있는 조건이기 떄문에 그대로 정렬해줍니다.

정렬된 자리 중 첫번째 우선순위의 자리를 선택하여 해당 학생의 자리로 지정한다.

정렬된 자리의 첫번째 우선순위 자리가 문제의 조건에 맞는 자리입니다.

따라서, 그 자리를 해당 학생의 자리로 지정해주면 됩니다.

학생들의 자리가 모두 지정되면, 각 학생들이 좋아하는 학생들을 다시 확인하며 만족도 계산을 진행한다.

마지막으로, 학생들의 자리와 각 학생들의 좋아하는 학생 리스트를 확인하면서 문제에서 요구하는 만족도 계산을 진행하면 됩니다.

💻코드

⏰ 시간 : 184 ms / 메모리 : 32572 KB

import sys
from collections import Counter
input = sys.stdin.readline


def search_empty_space(x, y, arr): # input으로 들어온 좌표의 주변 빈 칸 리스트 return
    ans = []
    pos = [[1, 0], [-1, 0], [0, 1], [0, -1]]
    for i in range(4):
        nx, ny = x + pos[i][0], y + pos[i][1]
        if arr[nx][ny] == 0:
            ans.append((nx, ny))
    return ans


N = int(input())
students = [list(map(int, input().split())) for _ in range(N ** 2)] # 각 학생들의 선호 학생 4명 리스트
arr = [[-1 for _ in range(N + 2)]] + \
      [[-1] + [0 for _ in range(N)] + [-1] for _ in range(N)] + \
      [[-1 for _ in range(N + 2)]] # 자리 리스트, -1으로 padding해서 좌표 조건문 제거
dic = {i: 0 for i in range(1, N ** 2 + 1)} # 각 학생들의 좌석 바로 접근 위한 dictionary
pos = [[1, 0], [-1,  0], [0, 1], [0, -1]] # 상하좌우 좌표

for student in students:
    candidates = []
    for i in range(1, 5): # 좋아하는 학생들 탐색
        if dic[student[i]]: # 좋아하는 학생의 자리가 정해진 경우
            # 좋아하는 학생의 상하좌우 자리 탐색하여 비어있는 자리라면 후보에 추가
            candidates += search_empty_space(dic[student[i]][0], dic[student[i]][1], arr)
    if not candidates: # 자신이 좋아하는 학생들이 모두 자리가 정해지지 않은 경우
        for i in range(1, N + 1): # 남아있는 칸들을 후보로 넣음
            for j in range(1, N + 1):
                if arr[i][j] == 0:
                    candidates.append((i, j))

    candidates = Counter(candidates).most_common() # 좋아하는 학생과 가장 많이 맞닿아 있는 자리 순
    # 가장 많이 중복되는 자리 내림 차순, 비어있는 자리 개수 내림 차순, 열과 행 오름 차순으로 정렬
    candidates.sort(key=lambda x: [-x[1], -len(search_empty_space(x[0][0], x[0][1], arr)), x[0][0], x[0][1]])
    dic[student[0]] = candidates[0][0]
    arr[candidates[0][0][0]][candidates[0][0][1]] = student[0]

ans = 0
for student in students: # 만족도 점수 계산
    likes = student[1:]
    x, y = dic[student[0]]
    count = 0
    for i in range(4):
        if arr[x + pos[i][0]][y + pos[i][1]] in likes:
            count += 1 # 상하좌우 자리에 좋아하는 학생이 있는 경우 count 1증가
    ans += 1 if count == 1 else 10 if count == 2 else 100 if count == 3 else 1000 if count == 4 else 0
print(ans)

📝코드 설명

변수

students : 학생들의 번호가 각 학생들이 좋아하는 학생들을 입력 그대로 넣어둔 2차원 리스트입니다. 이 리스트의 앞에서부터 학생들의 자리를 배정합니다.
arr : 학생들의 자리를 N X N으로 표현한 2차원 리스트입니다.
단, 리스트를 -1로 감싸주어 상하좌우 좌표 확인 시 유효한 좌표인지를 확인하는 조건문을 생략할 수 있도록 하였습니다.
값이 -1이면 padding 값, 0이면 비어있는 자리, 그 외 양수라면 해당 학생이 그 자리에 배정되었음을 의미합니다.
dic : {학생 번호 : [배정된 자리 좌표]}로 구성되어 있는 딕셔너리입니다.
arr 외에, 각 학생들이 배정된 자리의 좌표에 바로 접근할 수 있도록 각 학생들의 배정된 자리를 저장하는 딕셔너리를 사용하였습니다.
pos : 상하좌우 좌표를 쉽게 계산하기 위한 리스트