📌문제
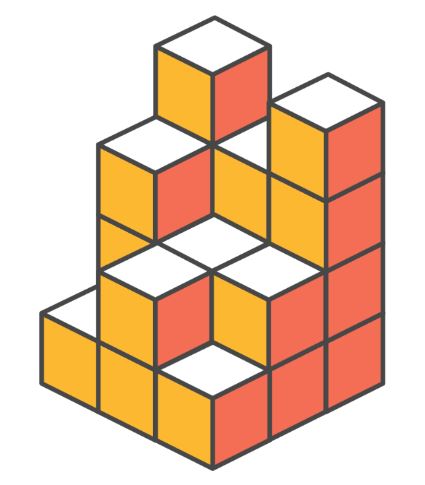
크기가 N×M인 종이가 있고, 종이는 1×1크기의 칸으로 나누어져 있다. 이 종이의 각 칸 위에 1×1×1 크기의 정육면체를 놓아 3차원 도형을 만들었다.
종이의 각 칸에 놓인 정육면체의 개수가 주어졌을 때, 이 도형의 겉넓이를 구하는 프로그램을 작성하시오.
위의 그림은 3×3 크기의 종이 위에 정육면체를 놓은 것이고, 겉넓이는 60이다.
입력
첫째 줄에 종이의 크기 N, M이 주어진다. 둘째 줄부터 N개의 줄에는 종이의 각 칸에 놓인 정육면체의 수가 주어진다.
출력
첫째 줄에 도형의 겉넓이를 출력한다.
제한
- 1 ≤ N, M ≤ 100
- 1 ≤ 종이의 한 칸에 놓인 정육면체의 수 ≤ 100
예제 입력1
1 1
1예제 출력1
6예제 입력2
3 3
1 3 4
2 2 3
1 2 4예제 출력2
60💡Idea
처음에는 만들어진 3차원 도형의 6면을 구하여 전부 더하는 식의 접근을 생각했었습니다.
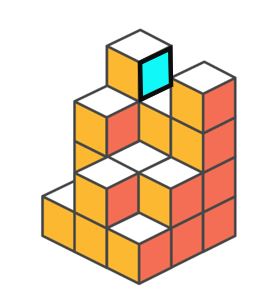
하지만 이런 식의 접근은 아래 예시에서 표시된 부분처럼 계산하지 못하는 부분이 생긴다는 것을 발견하였습니다.
따라서, 각 칸에 쌓여져 있는 정육면체들의 드러나 있는 모든 면을 각각 계산하여 문제를 해결해보았습니다.
각 칸에 쌓여져 있는 정육면체들의 드러난 면의 개수는, 사방에 있는 정육면체들의 개수를 사용하여 드러나있는 면들을 계산할 수 있었습니다.
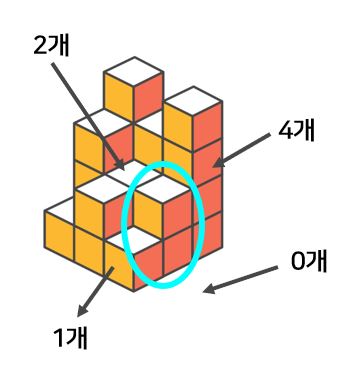
그림에 표시된 칸에 쌓여져있는 두 개의 정육면체들의 드러난 면의 개수를 구해봅시다! 이 때, 위와 아래의 면은 우선 제외하고, 정육면체들의 옆 면을 구해봅니다.
해당 칸의 사방에는 각각 4개, 2개, 1개, 0개의 정육면체들이 있습니다.
우리는 표시된 칸 보다 적은 수의 정육면체가 있는 칸들을 골라내고, 고른 칸들의 정육면체 개수와의 차를 구하게 되면 정답을 구할 수 있습니다.
즉, 표시된 칸보다 적은 수의 정육면체가 있는 곳은 1개와 0개가 있는 곳입니다. 그리고 각각의 개수 차는 1과 2입니다. 따라서, 표시된 칸의 드러나 있는 옆면의 개수는 3으로 볼 수 있습니다.
그리고 위와 아래의 면은, 해당 칸에 정육면체가 있기만 하면 2개를 추가해주면 됩니다.
최종적으로, 표시된 칸의 드러나있는 면의 개수는 총 5개라고 할 수 있습니다.
💻코드
- ⏰ 시간 : 88 ms / 메모리 : 30840 KB
import sys
input = sys.stdin.readline
N, M = map(int, input().split())
arr = [[0 for _ in range(M + 2)]] \
+ [[0] + list(map(int, input().split())) + [0] for _ in range(N)] \
+ [[0 for _ in range(M + 2)]]
ans = 0
pos = [[1, 0], [-1, 0], [0, 1], [0, -1]] # 사방으로 이동하기 위한 좌표
for i in range(1, N + 1):
for j in range(1, M + 1):
if arr[i][j] > 0: ans += 2 # 칸에 정육면체가 존재하면 위아래 면 2개 추가
for k in range(4): # 사방에 있는 정육면체 개수 확인
compare = arr[i][j] - arr[i+pos[k][0]][j+pos[k][1]]
if compare > 0: # 정육면체 개수가 현재 구하려는 칸의 개수보다 작은 경우
ans += compare # 개수의 차를 더해줌
print(ans)📝코드 설명
변수
arr: 입력되는 정육면체들의 개수를 담은 리스트입니다. 이 때, 가장자리 칸들의 사방을 확인하기 편리하도록 리스트를 0으로 감싸주었습니다.