[자료구조] 트라이(Trie)

수영·2022년 9월 28일

Trie 자료구조

자료구조

목록 보기

2/2

🤔트라이(Trie)란?

트라이(Trie)란 문자열을 저장하고 효율적으로 탐색하기 위한 트리 구조의 자료구조를 말합니다.

트라이는 래딕스 트리(Radix Tree), 접두사 트리(Prefix Tree), 혹은 탐색 트리(retrieval tree)라고도 합니다.
여기서 트라이의 Trie가 Retrieval에서 따온 문자라는 말도 있답니다!

이름에서도 알 수 있듯 트라이는 문자열 탐색🔍에서 굉장히 효율적인 구조를 가지고 있기 떄문에, 검색어 자동 완성, 사전에서 찾기, 문자열 검사 등에 활용이 된다고 합니다.

트라이의 형태

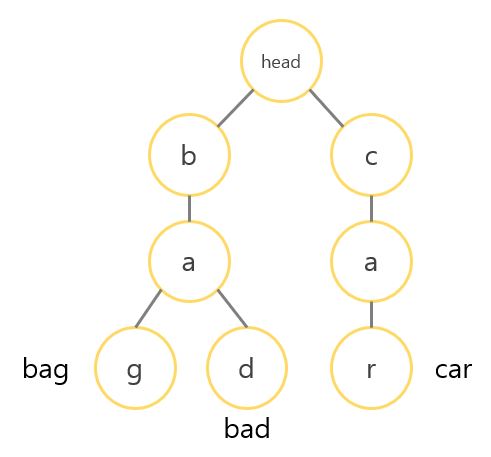
🙋‍♀️ 문자열 집합 {'bag', 'bad', 'car'}를 트라이로 구현해봅시다!

위 사진과 같이, 트라이는 한 문자열에서 다음에 나오는 문자가 현재 문자의 자식 노드가 되는 형태로 구성되어 있습니다.

즉, 트리의 head(root)에서부터 자식들을 따라가면서 생성된 문자열이 트라이 자료구조에 저장되어 있다고 볼 수 있습니다.

그리고 저장된 단어는 해당 단어의 마지막 글자에 함께 저장되어, 저장된 단어의 끝임을 알 수 있습니다.

이러한 트라이의 형태로 알 수 있는 중요한 속성 하나가 있는데, 그것은 바로 루트에서부터 내려가는 경로에서 만나는 글자들을 모으면 찾고자 하는 문자열의 접두사를 얻을 수 있다는 것입니다.

트라이의 장단점

장점

문자열 검색을 빠르게 할 수 있습니다.
문자열 탐색 시, 존재하는 모든 문자열을 하나하나씩 비교하여 탐색하는 것보다 훨씬 효율적인 시간복잡도를 가질 수 있습니다.
👉 만약 'bad'라는 단어를 탐색하고 싶다면, 제일 먼저 'b'를 찾고, 'b'의 자식들중에서 'a'를 찾고, 또 다시 'a'의 자식들 중에서 'd'를 찾는 식으로 탐색을 하면 됩니다.

단점

각 노드들이 자식들에 대한 포인터들을 배열로 저장하고 있기 때문에, 저장 공간의 크기가 큽니다.
👉필요한 총 메모리는
$O(포인터 크기 \times 포인터 배열 개수 \times 총노드의 개수)$ 가 됩니다.

👩‍🏫트라이 예제

🙋‍♀️ {'bag', 'bad' 'car'} 문자열을 순서대로 트라이에 추가해봅시다!

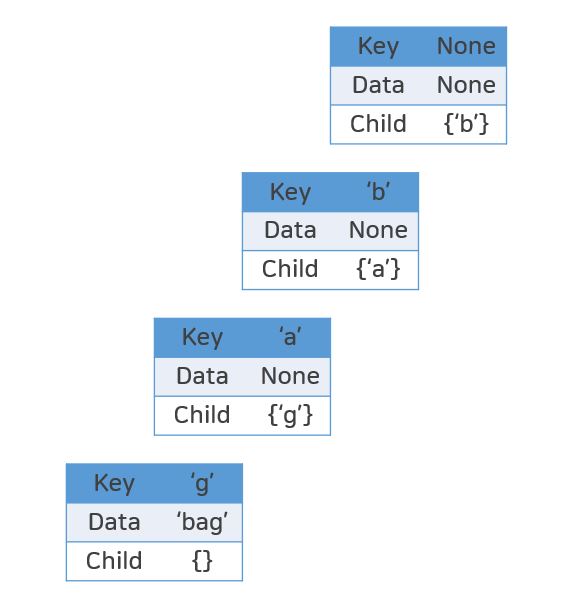
'bag' 추가하기

가장 위의 노드는 Head입니다. 따라서, Key와 Data는 None이고, Child의 값만 가집니다.

처음에 트라이는 Head만 존재하는 상태이기 때문에, 'bag'를 차례로 추가해주면 됩니다.

Head에는 Child에 'b'를, Key가 'b'인 노드는 Child로 'a'를, Key가 'a'인 노드는 Child로 'g'를 넣어줍니다.

그리고, Key가 'g'인 노드는 문자열이 끝났기 때문에 더이상 Child는 존재하지 않으며, 대신 문자열의 마지막임을 알리기 위하여 Data에 지금까지의 문자열인 'bag'를 추가해줍니다.

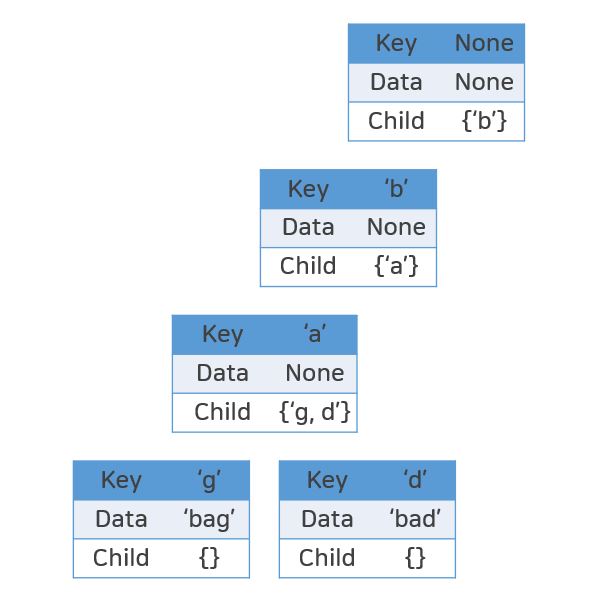
'bad' 추가하기

이미 트라이에는 'b'와 'a'가 존재합니다.
따라서, 따로 추가하지 않고 각 노드를 따라 아래로 이동합니다.

Key가 'a'인 노드의 Child에 'd'를 추가해줍니다. 그리고, Key가 'd'노드는 존재하지 않으므로, 'd'노드를 추가해줍니다.

Key가 'd' 노드에서 문자열이 끝났기 때문에 더이상 Child는 존재하지 않습니다. 대신, 문자열의 마지막이기 때문에, Data에 지금까지의 문자열인 bad를 넣어줍니다.

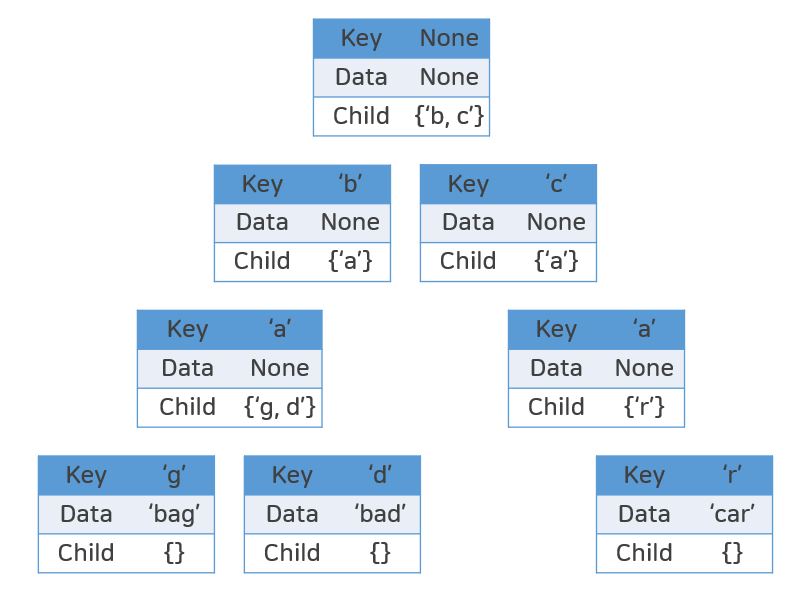
'car' 추가하기

Head의 Child를 확인해보면, 'c'는 존재하지 않기 때문에, Key가 'c'인 노드를 만들고 Head의 Child에도 'c'를 추가해줍니다.

그리고는 'bag'을 추가했던 것과 비슷하게 나머지 'a'와 'r'을 추가해줍니다.

⏰트라이 시간복잡도

제일 긴 문자열의 길이를 L, 총 문자열들의 수를 M이라 할 때 시간복잡도는 아래와 같습니다.

생성 시간 복잡도 : $O(ML)$
각 문자열을 트라이에 삽입하려면, 삽입하려는 문자열의 길이만큼만 노드를 따라가거나 추가해주면 됩니다. 따라서 각 문자열을 추가할 때의 시간복잡도는 $O(L)$ 입니다.
주어진 모든 문자열들을 삽입할 때의 시간복잡도는 $O(ML)$ 입니다.
문자열의 개수 M개에 대해서 M 번 삽입을 진행하기 때문입니다.

탐색 시간 복잡도: $O(L)$
문자열을 탐색할 때, 문자열의 길이만큼만 노드를 따라가며 탐색하기 때문에, $O(L)$ 만큼 걸립니다.

💻트라이 구현(python)

class Node(object):
    def __init__(self, key, data=None):
        self.key = key # 해당 노드의 key 값
        self.data = data # 해당 노드가 문자열의 마지막인지를 알 수 있는 필드
        self.children = {} # 해당 노드의 자식들로, {자식 key: 자식노드 자체}의 형태

class Trie(object):
    def __init__(self):
        self.head = Node(None) #처음 초기화는 head에 key가 None인 노드 생성

    def insert(self, string):
        current = self.head #head부터 읽기 시작
        for char in string:
            if char not in current.children: #문자가 children에 존재하지 않는 경우
                current.children[char] = Node(char) #children에 추가
            current = current.children[char] #해당 문자 노드로 이동
        #모든 문자 노드 추가 후, 마지막 노드의 data에 전체 문자열 추가
        current.data = string 
        
    def search(self, string):
        curr_node = self.head # head부터 찾기 시작
        for char in string:
            if char in curr_node.children: #문자가 children에 존재하는 경우
                curr_node = curr_node.children[char] #해당 문자 노드로 이동 
            else: return False #문자 노드가 존재하지 않는 경우 False 반환
        if curr_node.data != None: #끝까지 이동했을 때 data가 None이 아니라면
            return True # True 반환