2021.10.18 TIL
통계학
1. 데이터의 획득과 정리
1-1. 통계학 개요
-통계학의 연구 대상
모집단 (population) 으로부터 표본추출(sampling)을 통해 표본(sample)을 추려낸 후 통계량(Statistics)로부터 추론으로 모수(Parmaeters)를 얻어낸다.
1-2. 표본 추출
비용, 실현 가능성의 문제로 표본을 추출한다.
-단순 무작위 추출(Simple Random Sampling)
전체에 대한 무작위 추출로 난수표를 이용해 표본의 크기만큼 개체를 선택한다.
-충화 추출(Stratified Random Sampling)
데이터 내의 지정된 그룹 별 비율만큼 표본을 그룹 별로 선택한다.
-계통 추출(Systematic Sampling)
모집단의 크기를 원하는 표본의 크기로 나누어 표집 간격을 계산한 후 표집 간격 마다의 표본을 선택한다. 요소들이 추출 전 무작위가 아닌 주기성을 띄고 있으면 매우 어긋난 표본이 될 수 있다.
-군집 추출(Cluster Sampling)
모집단이 여러 소집단으로 구성되어있을 때 한 소집단 자체를 표본대상으로 선택한다. 비용 절감이 가능하다.
-충화 추출과 군집 추출
충화 추출은 군집간 이질성, 군집내 동질성 / 군집 추출은 군집간 동질성, 군집내 이질성을 갖추어야 올바른 표본을 추출할 수 있다.
변수
-변수의 타입
범주형 : 정성적,질적 자료로 빈도 중심이다. 문자열의 값을 갖는 경우가 많다. 단순 범주를 표시하는 명목형, 범주의 순서가 비교가 가능한 순서형으로 분류된다.
수치형 : 정량적,양적 자료로 셀수 있는 형태의 자료인 이산형, 수치로 연속적인 값을 갖는 연속형으로 분류된다.
1-3. 데이터 전처리
데이터 분석 작업 전 데이터를 분석하기 좋은 형태로 만드는 과정
-데이터 전처리의 주요 기법
정제(Cleansing), 통합(Intergration), 축소(Reduction), 변환(Transformation)
-데이터 전처리의 예
결측값(Missing Value) : 존재하지 않고 비어 있는 상태로 DB상에서 Null 값인 경우. 데이터를 채울 필요가 있다. 완전 무작위 결측, 무작위 결측, 비 무작위 결측으로 분류된다.
결측값 처리 방법
- 평균 대체법 : 평균 값으로 null 값을 채운다. 응답률 높은 집단의 영향력이 커질 수 있고 표준편차가 과소 추정 될 수 있다.
- 핫 덱 대체법 : 관측값 중 결측값, 특성이 비슷한 것을 무작위 추출하여 대체한다.
- 해당 데이터 행을 모두 제거하거나 수작업으로 제거한다.
이상값(Outlier) : 대표적인 잡음 요소로 경향성 훼손을 발생시킬 수 있다.
이상값 탐지 방법
- 수치적 탐지 방법
IQR기준 : IQR 기반의 기법으로 Q1,Q2,Q3의 세 점으로 관측값을 4부분으로 나눈 후 Q1과 Q3를 기준으로 상,하한을 정하여 이상값을 규정한다. 상,하한을 정하는 방법에는 Tukey 방법과 Carling 방법이 있다.
Z-Score : 데이터를 정규화 하여 Z-score를 기준으로 이상값을 규정한다.- 확률, 분포를 이용하는 방법
- 머신 러닝을 이용하는 방법
이상값 처리 방법
- 제외(trimming) : 처리가 간단하지만 정보 손실이 발생하고 추정량이 왜곡될 수 있다.
- 대체(winsorization) : 이상값을 정상값 중 최소, 최대로 대체한다.
- 변수변환 : log변환, 제곱근 변환 등으로 분포의 왜도를 줄인다.
- 변수구간화 : 그래프에서 한 기둥을 구간화하여 최소,최대를 개방 구간으로 만든다.
-축소
Sampling : 데이터의 양이 너무 많아 분석이 어렵거나 소요 시간이 길 경우 분석에 적절하도록 축소한다.
차원의 저주 : 데이터의 차원이 늘어나면 해당 공간의 크기가 기하급수적으로 증가하고 데이터의 밀도는 희박해져 데이터 분석에 필요한 데이터의 수가 기하급수적으로 증가한다.
-결합
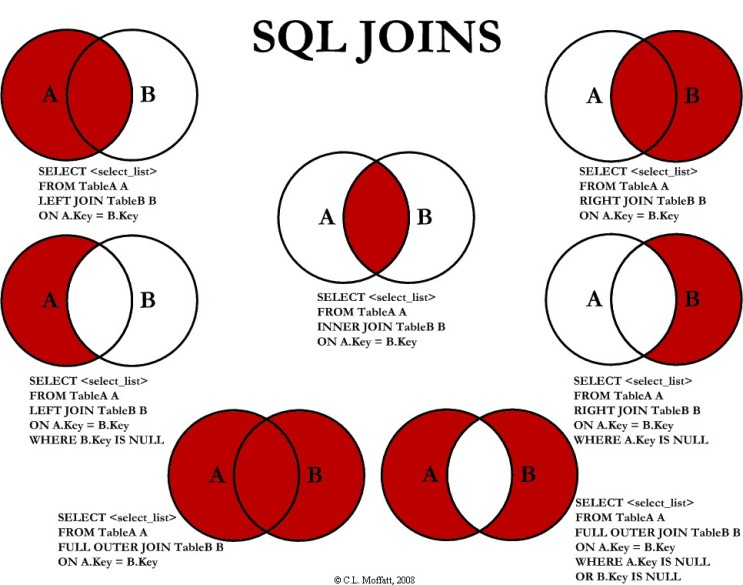
출처 : http://www.codeproject.com/KB/database/Visual_SQL_Joins/Visual_SQL_JOINS_orig.jpg
테이블 구조를 가친 데이터 간의 공통 요소,컬럼,변수를 기준으로 데이터 테이블을 합하여 하나의 데이터로 만든다.
-파생변수 생성(Feature Engineering) : 변환의 방식 중 하나로 차원을 늘린다.
이미 수집된 변수를 활용해 새로운 변수를 생성하는 것으로 주관적일 수 있기 때문에 논리적 타당성을 반드시 갖추어야 한다.
-요약 변수 : 원 데이터를 분석 필요에 맞게 종합하여 데이터의 수준을 달리하여 종합하는 경우가 많다.
2.기술 통계 (Descriptive Analysis)
2-1. 기초 통계
-분포 분석(수치형 변수)
단일 수치형 변수에 대한 분석은 대표값과 흩어짐 정도의 파악과 비교로 시작한다.
위치 통계량(중심 경향성) : 대표값과 그 위치 ( 평균,중앙값,최빈값) 에 대한 정보
변이 통계량 : 데이터가 대표값으로부터 흩어져 있는 정도로 범위, 분산, 표준편차 등을 포함한다.
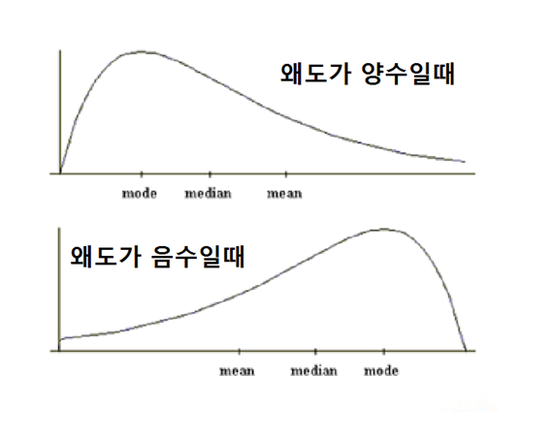
모양 통계량 : 데이터의 분포 모양, 대칭성을 설명하며 왜도,첨도 등을 포함한다.
위치 통계량 - 평균의 종류
- 산술 평균 : 주어진 수의 합을 수의 개수로 나누어, 계산이 쉽고, 수학적으로 활용하기 편하지만 극단적인 값에 민감하다.
- 기하 평균 : N개의 양수 값을 모두 곱한것의 N 제곱근, 성장율 등의 평균을 구하는데 사용된다.
- 조화 평균 : 주어진 수들의 역수의 산술 평균의 역수로 평균적인 변화율을 구하는 데 사용된다.
- 가중 평균 : 일률적 평가가 어려울 때, 차지하는 비중이 다를 때 사용된다. 물가지수, 주가지수,수익률 등의 계산에 사용된다.
위치 통계량 - 중심 경향성
- 중앙값(Median) : 데이터를 순서대로 나열하여 가운데 있는 값
- 최빈값(Mode) : 자료에서 빈도가 가장 많은 관측지, 존재하지 않을 수 잇고, 유일한 값이 아닐 수도있어 보조적인 지표로 사용된다.
중앙값과 최빈값은 극단적 이상치가 있을 경우는 중앙값이 우선되어 사용될 수있고, 자료의 분포가 비대칭일 경우 평균의 보조 자료로 이용된다. 개방 구간을 갖는 경우에는 중앙값이나 최빈값을 대표값으로 사용하기도 한다.
변이 통계량 (퍼짐 정도)
- 범위 : 자료에서 최대치와 최소치의 차이로 이상치에 민감
- 중간범위 : 최대치와 최소치의 합을 2로 나눈값, 이상치에 민감
- 평균절대편차 : MAD(Mean Absolute Deviation)라고 하며 편차의 절대값을 모든 자료에 대해 구한 절대편차합을 평균낸 값.
- 분산 : 모든 편차를 제곱해 합한 후 자료의 총 수로 나눈 값 s^2 로 표기한다. 분산이 작으면 자료의 변동이 심하지 않다는 것을 의미한다. 제곱으로 구하기 때문에 원자료와 단위가 달라진다. 표본 분산은 모분산을 구할때 추정치로 사용된다.
표본 분산은 모분산을 구할 때와 달리 n-1(자유도)를 사용하는데, n을 사용하면 모분산을 과소추정하게되기 때문이다.- 표준편차 : 분산의 양의 제곱근으로 단위가 달라지는 분산을 다른 통계량들과 비교하기 위해 원래 자료의 단위로 환원한다.
- 자료가 흩어질수록 범위,중간범위,분산, 표준편차가 커진다.
- 자료가 평균 주위로 집중되면 범위, 중간범위, 분산, 표준편차가 작아진다.
- 자료의 범위가 동일하면 범위, 중간범위, 분산, 표준편차는 0이다.
- 범위, 중간범위, 분산, 표준편차는 양수다.
변동 계수 : coefficient of variation(CV) 로 서로 다른 데이터 간의 편차를 비교하기 위해 사용된다. 표준편차를 표본 평균, 모평균으로 나누면 각각 표본변동계수, 모변동계수가 된다.
위치 통계량 (분포의 모양)
출처 : https://m.blog.naver.com/moses3650/220880815585