[알고리즘] DFS와 BFS

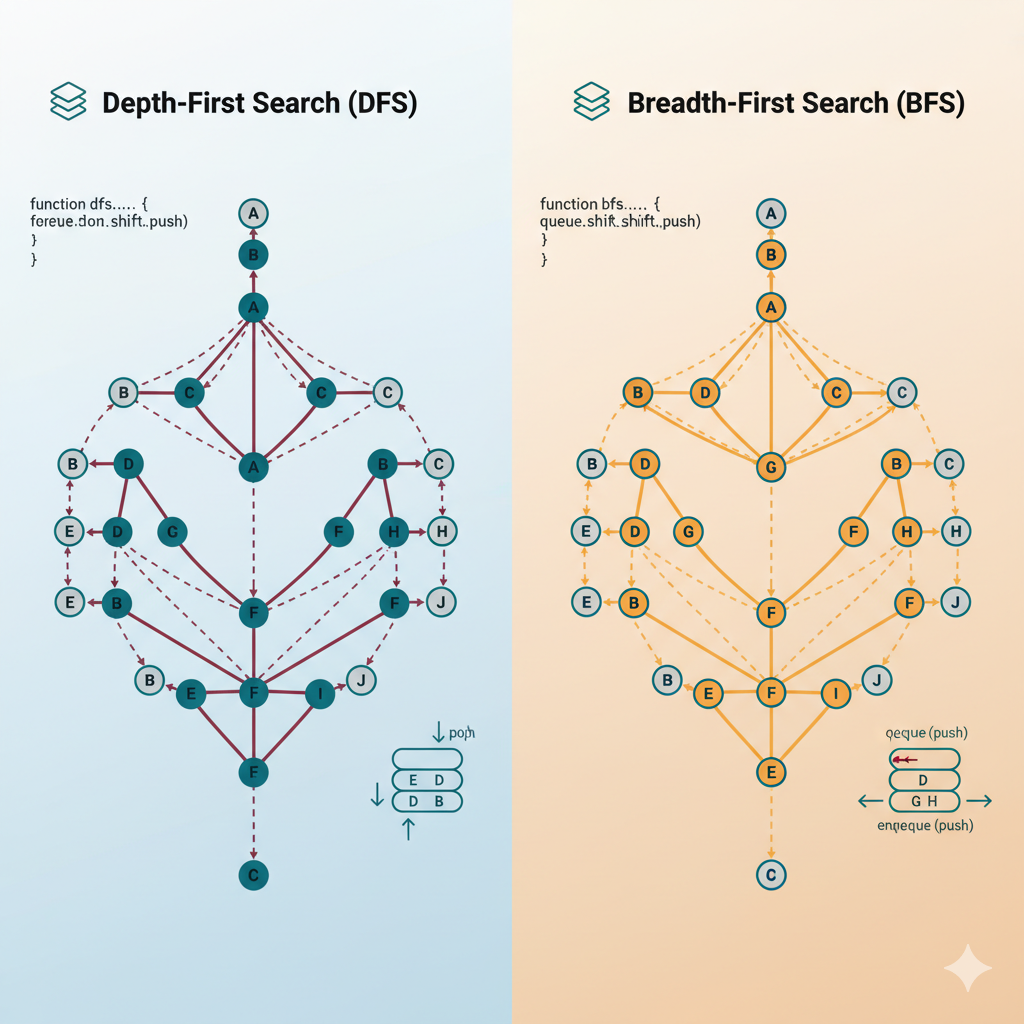
DFS와 BFS는 알고리즘의 기초이자 핵심이라고 할 수 있다.

1. DFS (Depth-First Search)

• DFS는 그래프 탐색 알고리즘 중 하나로, '깊이'를 우선으로 탐색한다.
• 다시 말해, 한 노드에서 시작하여 다음 분기로 넘어가기 전에 해당 분기를 완벽하게 탐색하는 방식이다.
• 동작 원리: 스택(Stack) 또는 재귀 함수를 이용
• 활용 예시: 미로 찾기, 모든 노드를 방문하는 경우, 사이클(Cycle) 판별 등

const graph = {
  'A': ['B', 'C'],
  'B': ['A', 'D'],
  'C': ['A', 'G', 'H'],
  'D': ['B', 'E', 'F'],
  'E': ['D'],
  'F': ['D'],
  'G': ['C'],
  'H': ['C', 'I'],
  'I': ['H']
};


function dfs(graph, startNode, visited = new Set(), result = []) {
  if (visited.has(startNode)) {
    return; 
  }

  visited.add(startNode);
  result.push(startNode);

  (graph[startNode] || []).forEach(neighbor => {
    if (!visited.has(neighbor)) {
      dfs(graph, neighbor, visited, result);
    }
  });
  
  return result;
}

# 그래프 (인접 리스트) 예시
graph = {
    'A': ['B', 'C'],
    'B': ['A', 'D'],
    'C': ['A', 'G', 'H'],
    'D': ['B', 'E', 'F'],
    'E': ['D'],
    'F': ['D'],
    'G': ['C'],
    'H': ['C', 'I'],
    'I': ['H']
}

# 방문한 노드를 저장할 집합(Set)
visited = set()

def dfs(graph, node):
    if node not in visited:
        visited.add(node)
        
        for neighbor in graph.get(node, []):
            dfs(graph, neighbor)

2. BFS (Breadth-First Search)

• BFS는 그래프 탐색 알고리즘 중 하나로, '너비'를 우선으로 탐색.
• 시작 노드에서 가까운 노드들을 먼저 모두 탐색한 후, 점차 먼 노드로 이동하는 방식.
• 동작 원리: 큐(Queue) 자료구조를 이용
• 활용 예시: 최단 경로 찾기 (가중치가 없는 그래프에서), 미로 최단 경로, 최소 횟수 문제 등

function bfs(graph, startNode) {
  const queue = [startNode];
  const visited = new Set([startNode]);
  const result = [];

  while (queue.length > 0) {
    const node = queue.shift();
    result.push(node);

    (graph[node] || []).forEach(neighbor => {
      if (!visited.has(neighbor)) {
        visited.add(neighbor);
        queue.push(neighbor);
      }
    });
  }
  
  return result;
}

from collections import deque

def bfs(graph, start_node):
    queue = deque([start_node])
    visited = {start_node}
    result = []
    
    while queue:
        node = queue.popleft()
        result.append(node)
        print(f"방문 노드: {node}")
        
        for neighbor in graph.get(node, []):
            if neighbor not in visited:
                visited.add(neighbor)
                # 방문하지 않은 노드는 큐의 맨 뒤에 추가합니다 (append).
                queue.append(neighbor)
                
    return result