[CS231n]Lecture 7. SGD와 Momentum, Adagrad, RMSProp, Adam

SGD

• local minimum 이나 saddle point에서 멈출 수 있다.

SGD + momentum

• velocity 개념을 도입하여, gradient가 0이 되어도 velocity에 의해 local minimum으로부터 벗어날 수 있게 한다.

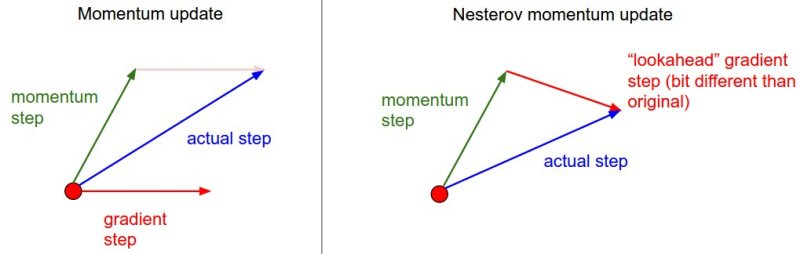
Momentum 방식에서는 이동 벡터 vt 를 계산할 때 현재 위치에서의 gradient와 momentum step을 독립적으로 계산하고 합치는 반면, NAG에서는 momentum step을 먼저 고려하여, momentum step을 먼저 이동했다고 생각한 후 그 자리에서의 gradient를 구해서 gradient step을 이동

Nesterov momentum

• velocity를 업데이트하기 위해 이전의 velocity$(ρv_t)$와$(x_t + \rho v_t)$에서의 gradient를 계산

• $x_{t+1}$은 위에서 계산된 $v_{t+1}$로 업데이트

• 변수 조정을 통해 loss와 gradient를 같은 점에서 계산할 수 있다.

$\rho$ : 0.9 나 0.99 가 이용됨.
$\alpha$ : 가중치. 최근의 gradient에 더 크게 부여됨.

AdaGrad

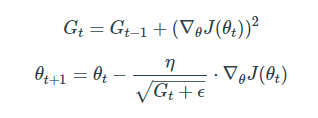
• Adagrad(Adaptive Gradient)는 변수들을 update할 때 각각의 변수마다 step size를 다르게 설정해서 이동하는 방식
• 지금까지 많이 변화하지 않은 변수들은 step size를 크게 하고, 지금까지 많이 변화했던 변수들은 step size를 작게 하자
• word2vec이나 GloVe 같이 word representation을 학습시킬 경우 단어의 등장 확률에 따라 variable의 사용 비율이 확연하게 차이나기 때문에 사용됨
• 제곱해서 더한걸 gradient로 삼고,
  dx / sqrt(grad_squared) 값을 업데이트

RMSprop

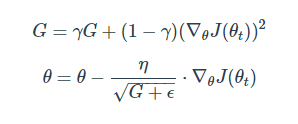
• Adagrad의 단점을 해결하기 위한 방법
• Adagrad의 $G_t$ 값이 너무 커지면 gradient가 0이 될 수 있음
• Adagrad의 식에서 gradient의 제곱값을 더해나가면서 구한 Gt 부분을 합이 아니라 지수평균으로 바꾸어서 대체한 방법

Adam

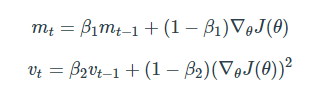
• RMSProp과 Momentum 방식을 합친 알고리즘

• $m_t$, $v_t$를 unbiased 하게 만들어주는 작업이 추가됨

• gradient 자리에 $\hat m_t$, $G_t$ 자리에 $\hat v_t$
  

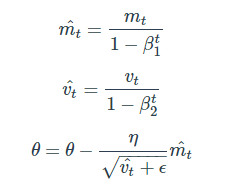
• 보통 β1 로는 0.9, β2로는 0.999, ϵ 으로는 $10^{−8}$ 정도의 값을 사용
  

Reference

• http://shuuki4.github.io/deep%20learning/2016/05/20/Gradient-Descent-Algorithm-Overview.html
• CS231n Lecture 7 lecture note.