이진 탐색 [binary search]

[do it 알고리즘 3-3]

이진 탐색?

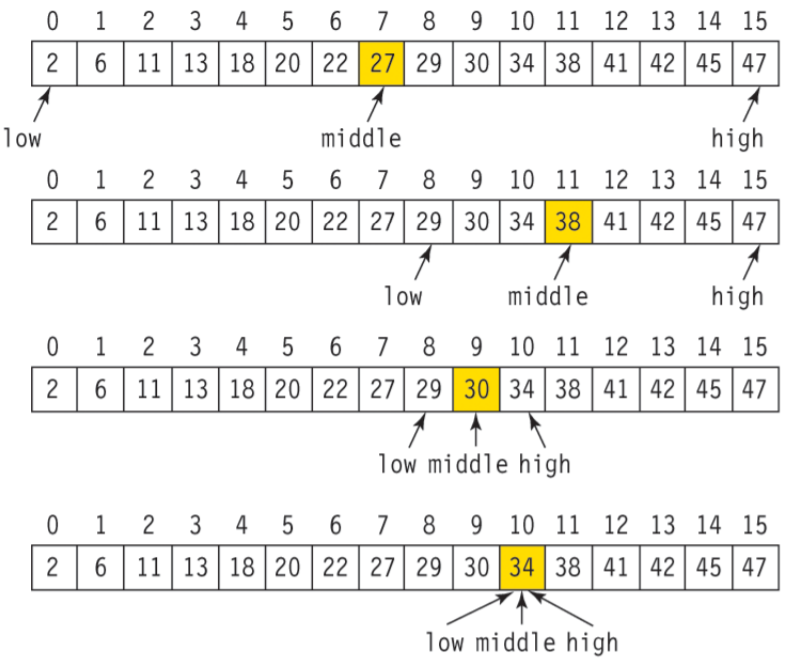
앞에서부터 순차적으로 값을 찾아나가는 선형탐색과 달리, middle값을 정해 중간에서부터 대소를 비교하여 찾을 범위를 줄여나간다.

시간복잡도

찾을 범위의 길이가 N일 때 최대 몇 번 반복하면 값을 찾을 수 있을까?
-> N을 몇 번 2로 나눴을 때 1이 되는가?

따라서 시간복잡도는 logN으로 선형탐색보다 빠르다.
ex) 길이가 1024인 리스트에서 선형탐색으로 값을 찾으면 최대 1024번 비교해야 하지만,

※ 값의 대소를 비교해 위치를 찾는 방식이므로 데이터가 미리 정렬되어있어야 사용 가능하다.

순서

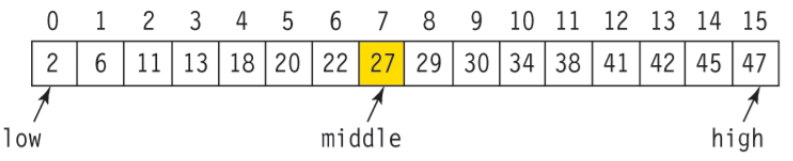
1. 탐색할 리스트 a의 범위에서 가장 왼쪽의 인덱스 low와 가장 오른쪽의 high를 정하고 low+high//2한 값을 middle로 정한다.

2. key값과 a[middle]을 비교하여 어느 쪽이 더 큰 지 알아낸다.

• a[middle]보다 작다면 앞부분만 탐색하도록 high의 값을 조정하고,
• a[middle]보다 작다면 뒷부분만 탐색하도록 low의 값을 조정한다.

if key > a[middle] : low = middle + 1
elif key > a[middle] : high = middle - 1

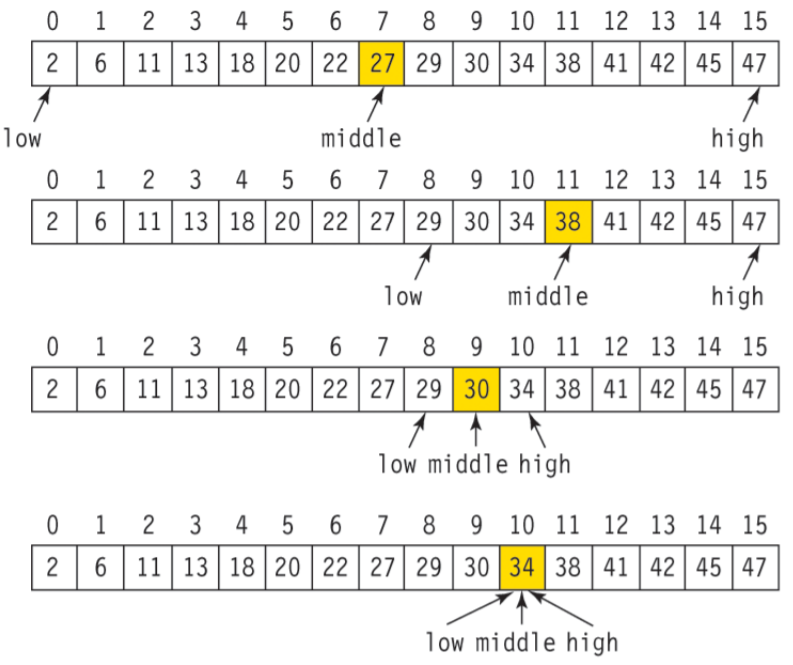
3. 1, 2의 과정을 반복한다. a[middle]과 key의 값이 같다면 탐색 완료

※ low가 high보다 커지면 리스트에 찾는 값이 없었을 것으로 탐색이 종료되어야 한다.
ex) 위의 예시의 마지막 그림에서 찾던 값이 34가 아닌 32라면, high = middle - 1 이므로 high는 9, low는 10을 가리키게 된다.

실습

[백준] https://www.acmicpc.net/problem/1920 [수 찾기]

n = int(input())
a = list(int(i) for i in input().split())
m = int(input())
b = list(int(i) for i in input().split())
list.sort(a)
# a는 검색할 리스트이므로 정렬해야함
# b는 원소를 가져와서 a에서 검색할 것이므로 정렬 필요X

for i in range(m):
	low = 0
	high = n - 1
	while True:
		mid = (low+high)//2
		if b[i] ==  a[middle]:
			print('1')
			break
		elif b[i] < a[middle]:
			high = middle-1
		else:
			low = middle+1
		if low > high:
			print('0')
			break