[백준] https://www.acmicpc.net/problem/1914
세 개의 장대가 있고 첫 번째 장대에는 반경이 서로 다른 n개의 원판이 쌓여 있다. 각 원판은 반경이 큰 순서대로 쌓여있다. 이제 수도승들이 다음 규칙에 따라 첫 번째 장대에서 세 번째 장대로 옮기려 한다.
- 한 번에 한 개의 원판만을 다른 탑으로 옮길 수 있다.
- 쌓아 놓은 원판은 항상 위의 것이 아래의 것보다 작아야 한다.
이 작업을 수행하는데 필요한 이동 순서를 출력하는 프로그램을 작성하라. 단, 이동 횟수는 최소가 되어야 한다.
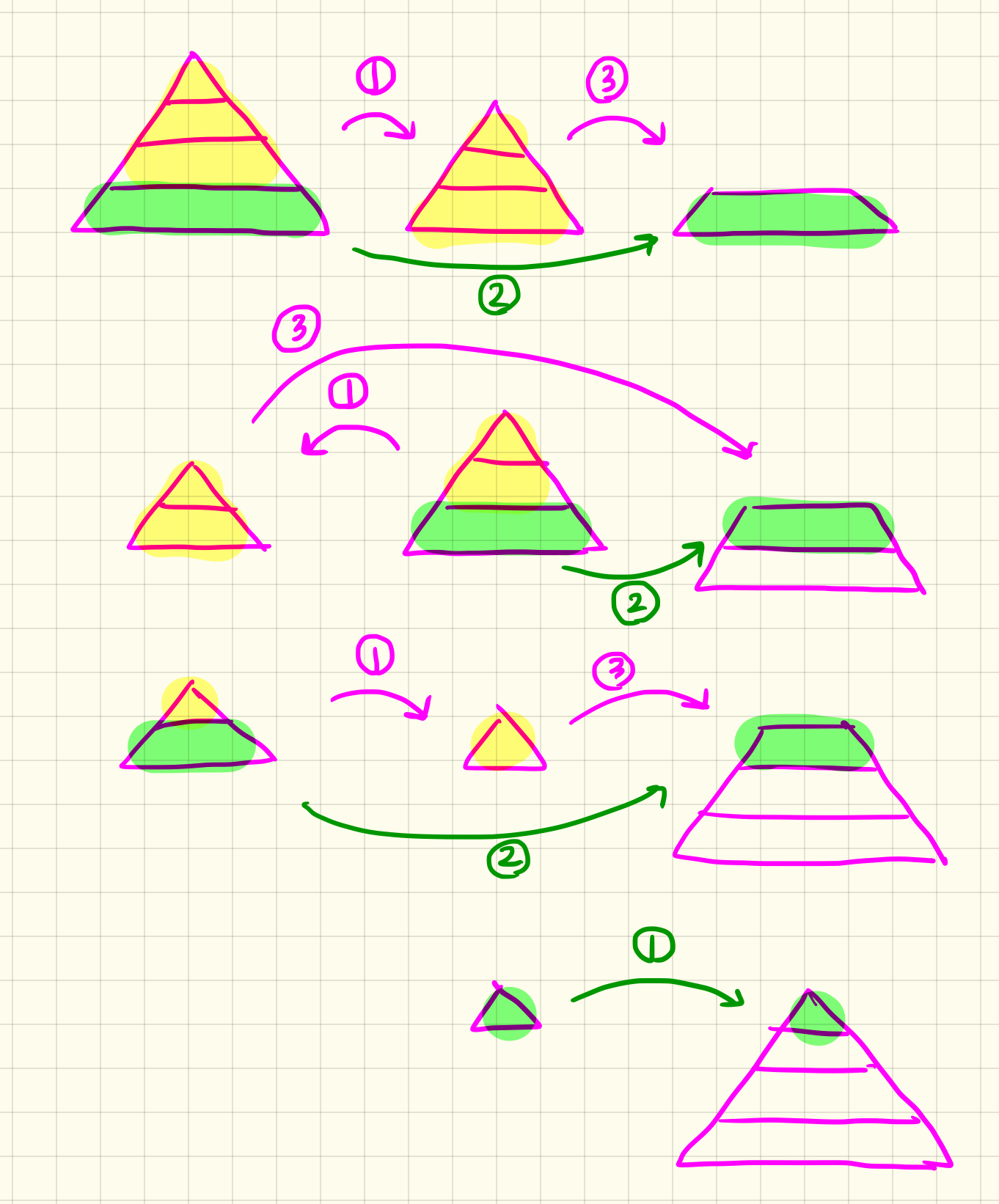
아래 그림은 원판이 5개인 경우의 예시이다.

하노이의 탑은 다음과 같은 규칙을 찾을 수 있다.
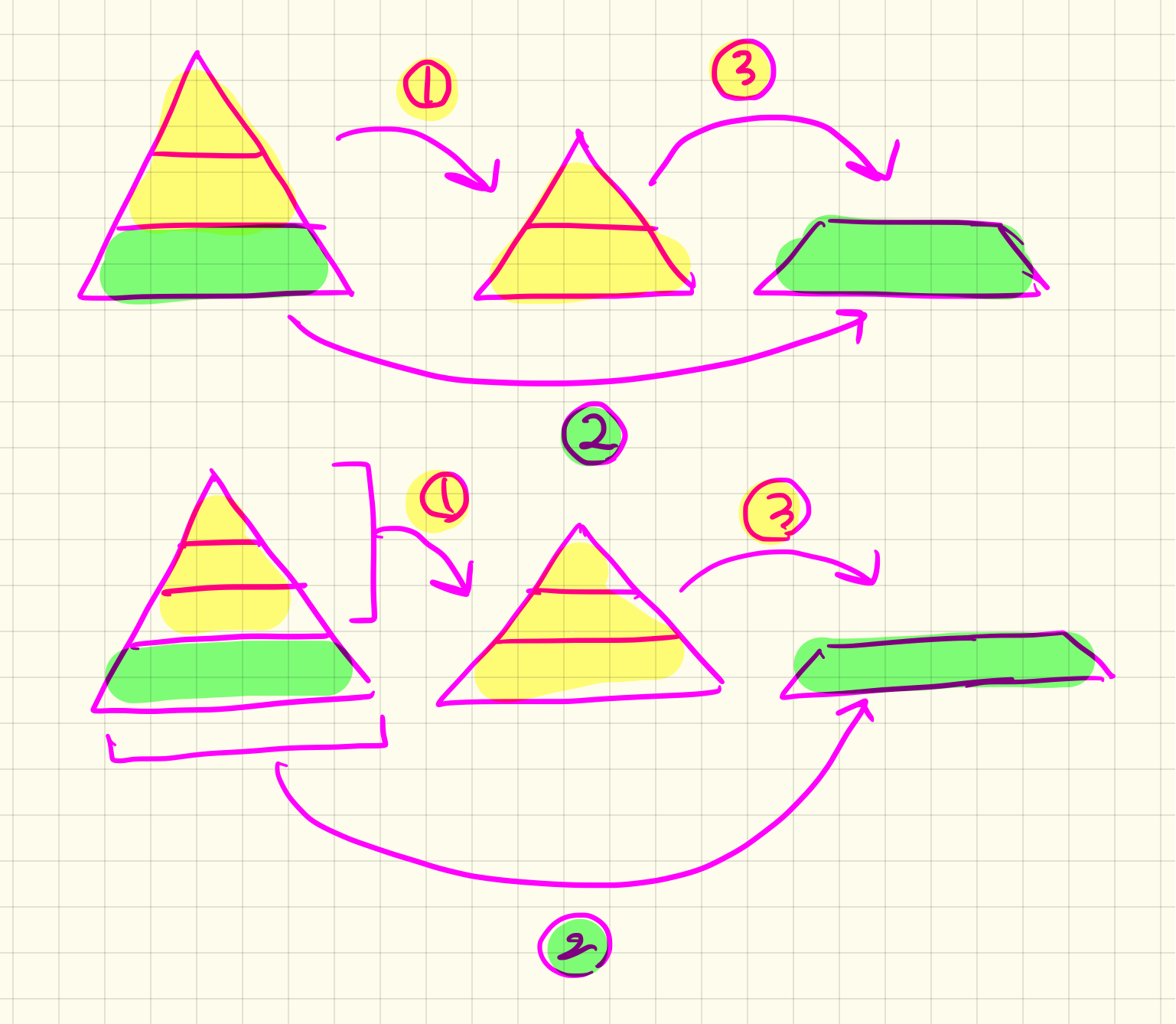
장대 3개를 차례대로 1, 2, 3이라고 부를 때,
원판 n개를 장대 1에서 3까지 옮기려면
- (1) 먼저 n-1개를 남는 자리인 2로 치운 뒤,
- (2) 맨 아래의 1개를 목적지 3으로 옮기고,
- (3) 남는 자리에서 n-1개를 다시 목적지 3으로 가져온다.
그리고 이 과정은 n > 1인 경우에 모두 적용되므로 이 문제를 재귀적으로 해결할 수 있다
(원판이 1개라면 바로 목적지로 옮길 수 있다)
n = 4
def hanoi(n, start, end, left):
# 리턴 조건
if n == 1:
print(f'{n}번째 원판을 {start}에서 {end}로 이동')
return
else:
# 재귀문에서 반복할 것
hanoi(n-1, start, left, end)
print(f'{n}번째 원판을 {start}에서 {end}로 이동')
hanoi(n-1, left, end, start)
hanoi(n, 1, 3, 2)
n이 3일 경우와 n이 4일 경우를 출력해보면 각각 다음과 같이 나온다.
n = 3
1번째 원판을 1에서 3로 이동
2번째 원판을 1에서 2로 이동
1번째 원판을 3에서 2로 이동
3번째 원판을 1에서 3로 이동
1번째 원판을 2에서 1로 이동
2번째 원판을 2에서 3로 이동
1번째 원판을 1에서 3로 이동
n = 4
1번째 원판을 1에서 2로 이동
2번째 원판을 1에서 3로 이동
1번째 원판을 2에서 3로 이동
3번째 원판을 1에서 2로 이동
1번째 원판을 3에서 1로 이동
2번째 원판을 3에서 2로 이동
1번째 원판을 1에서 2로 이동
4번째 원판을 1에서 3로 이동
1번째 원판을 2에서 3로 이동
2번째 원판을 2에서 1로 이동
1번째 원판을 3에서 1로 이동
3번째 원판을 2에서 3로 이동
1번째 원판을 1에서 2로 이동
2번째 원판을 1에서 3로 이동
1번째 원판을 2에서 3로 이동
n = 3일 때는 1번째 원판이 3으로 이동하며 시작하고, n = 4일때는 2로 이동하며 시작한다.
왜냐하면 n개의 원판을 옮기는데
n번째 원판은 2^0번
n-1번째의 원판은 2^1번
n-2번째 원판은 2^2번
n-3번째 원판은 2^3번
...
결국 n개의 원판을 움직일 때 필요한 움직임의 최소값은 2**n - 1(2^n -1)이고, 이는 홀수이기 때문에
n = 3으로 시작했을 때의 n = 3원판더미의 시작점과 n = 4에서 시작했을 때의 n = 3더미의 시작점이 달라지게 된다.
n개의 원판을 움직일 때 n-1원판은 2번 움직이는데, 이 중 1번은 end로 돌아가는 비용이니 결국 n-1의 기둥이 쌓이는 left기둥은 end인 3을 제외하고 1과 2 사이에서 start가 계속 변화한다고 생각해도 된다.