5.1 기본 개념
Indexing mechanism
- 데이터 접근을 신속하게 하는 기능 제공
- <.search-key, pointer> 양식
- Index 파일은 원본 파일보다 크기가 훨씬 작아야 함
- Ordered Index: 검색 키는 정렬된 순서로 저장
- Hash Index: 검색 키는 정렬된 순서가 아닌 버킷 전체에 분산
Index Evaluation Metrics
지원되는 액세스 유형
- 일치 질의 형태(exact match query)
- 범위 질의 형태(range query)
액세스 시간
삽입/삭제 시간
공간 오버헤드
정렬 색인 (Ordered Index)
Index record가 정렬되어 저장되는 구조
-
Clustering 색인
정렬색인 정렬 순서와 동일
(데이터 record를 정렬하여 데이터 File을 저장)
데이터 File당 최대 한개 -
Non-Clustering 색인
데이터 record가 정렬되지 않는 상태 저장
데이터 File에 다수개 존재
탐색키 구성 방법 기준으로 밀집색인/희소색인으로 구분 가능
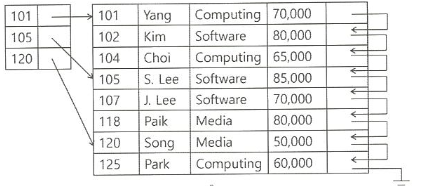
밀집 색인 (Dense Index)
모든 탐색키 값에 대해 Index record(entry)가 Index에 존재하는 경우
ex) 교수번호를 탐색키로 하여 색인 엔트리가 색인에 존재 -> 밀집 색인
ex) deptName을 탐색키로 하여 색인 엔트리가 색인에 존재 -> 밀집 색인
희소 색인 (Sparse Index)
모든 탐색키 값에 대한 Index record(entry)가 Index에 없는 경우
데이터가 탐색키 기준으로 정렬되어 있지 않은 File에 희소 색인을 구성하는 것은 의미없음
- Pros: 공간을 적게 차지
- Cons: 검색시간이 오래걸림 (entry Index에 없으면 데이터 File을 검색해야 함)
ex) 검색키 기준으로 정렬되어 있다면
희소 색인을 블록에 속하는 가장 적은 값으로 구성
-> 오버헤드: 블록 내 연산 < 메인 메모리 연산
-> 희소색인의 단점 보안
다단계 색인 (Multilevel Index)
Index File을 대상으로 한 단계 상위 Index를 구성
(색인 File에 entry가 많을 경우)Index File은 검색키 기준 정렬
-> 상위 계층의 색인 구성은 희소 색인으로 구성
(크기를 줄임)ex) 원 데이터 및 Index 데이터 모두 블록 단위로 처리
색인 갱신
Deletion
삭제되는 데이터 record가 마지막 record인 경우
- 밀집 색인인 경우:
삭제하는 record에 대한 관련 색인 record도 삭제 - 희소 색인인 경우:
삭제하는 record에 대한 Index entry가 희소 색인에 있는 경우: 색인 갱신 연산 필요 O
삭제하는 record에 대한 Index entry가 희소 색인에 없는 경우: 색인 갱신 연산 필요 X
 ex) 희소 색인인 경우
ex) 희소 색인인 경우
Insertion
삽입할 키 값을 조회
- 밀집 색인인 경우:
search-key값이 없으면 삽입 - 희소 색인인 경우:
Index가 File의 각 블록에 대한 항목을 저장 ->
새 블록을 만들면 첫 번째 search-key 값이 Index에 삽입
새 블록을 만들지 않으면 Index 변경 필요 X
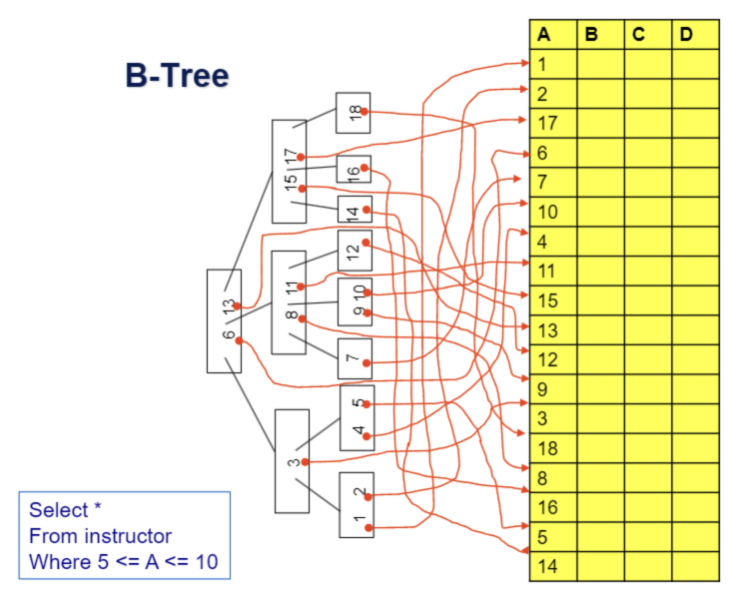
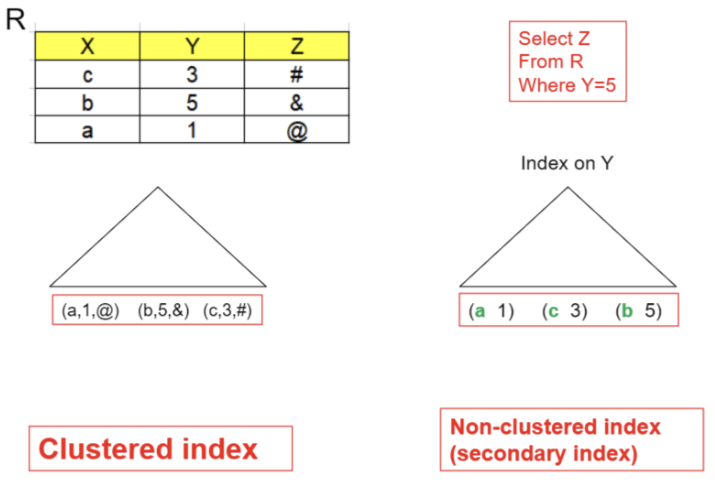
이차 색인 (Secondary Index)
Index record 순서대로 데이터 record 순서를 정렬하지 않은 Index
(어떤 색인이던 색인 record는 항상 정렬되어야 함)
- 색인 개수 제한 없이 생성 가능
- 반드시 밀집 색인 형태:
데이터 record 저장 순서와 색인 record 저장 순서가 다르므로ex) 포인터는 bucket을 pointing하고 bucket이 record를 pointing하는 구조
 (Index record가 간접적으로 데이터 record를 pointing함)
(Index record가 간접적으로 데이터 record를 pointing함)
주색인(primary Index)와 이차색인(secondary Index) 비교
-
Index를 사용하면 데이터 검색 시간이 향상됨
-
Index Update는 DB수정에 오버헤드 부과
(-> 파일을 수정할 때 파일의 모든 인덱스를 업데이트하기 때문) -
Primary Index는 순차탐색(Sequential scan)에 효율적
-
Secondary Index는 순차탐색(Sequential scan)에 많은 비용
(+ 이차 색인 레코드 순서대로 데이터 파일을 전체 탐색하면 동일 데이터 블록을 1회 이상 검색 가능)
5.2 B⁺-트리 색인
Balanced tree
데이터 변경을 유연하게 대처할 수 있음 (지역적 변경을 하기 때문)
B-tree 색인군
- B-tree
- B⁺-tree
- B*-tree
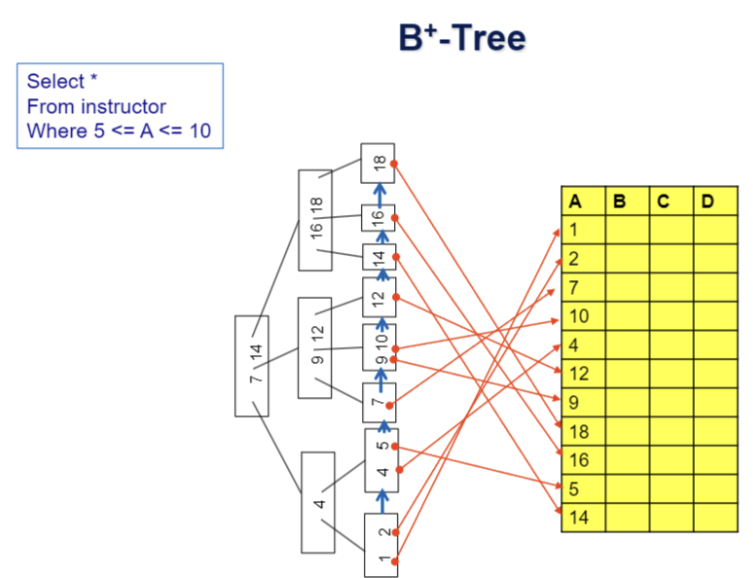
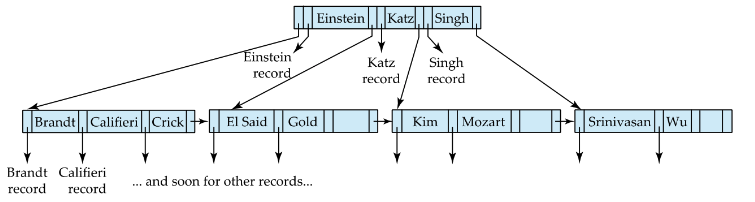
B⁺ Tree 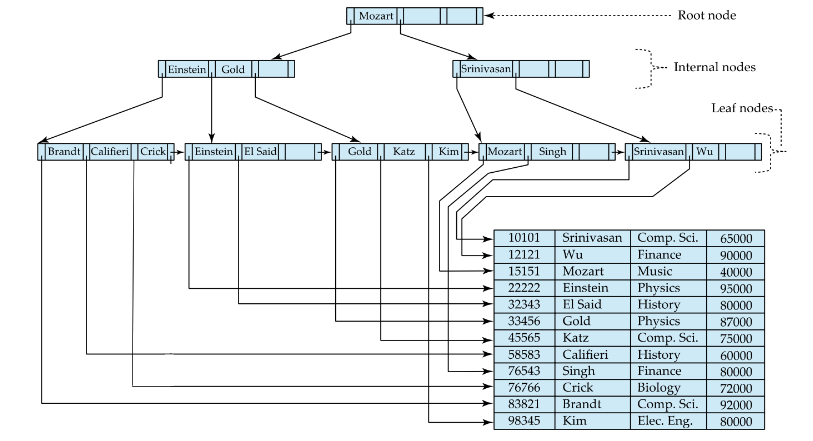
상기 그림은 n(pointer) n-1(key)인 B⁺ 트리의 예제
Root 노드부터 모든 Leaf node까지의 경로의 길이는 일정
(높이가 높아질 수록 성능 저하)
- Root node와 내부 node: 희소 색인 구조
- leaf node: 밀집 색인 구조
-> leaf node에만 데이터를 저장하고 leaf node가 아닌 node에서는 자식 포인터만 저장
순차 검색을 효율적으로 할 수 있게 됨
Root 노드는 최대 2개 이상의 자식
Root 노드와 Leaf node를 제외한 각 노드는 ⌈ n/2 ⌉ ~ n 개의 자식을 가짐
Leaf node는 ⌈ (n-1)/2 ⌉ ~ n-1 개의 키를 가짐
-> 균형을 위함
데이터의 삽입/삭제 연산으로 인해 특성을 유지하기 위해 트리 재구성을 할 수도 있음
B⁺ Tree 구조 
leaf node가 아닌 node에 대하여 Pi는 자식 node에 대한 포인터를 의미 -> page id
leaf node의 Pi는 record에 대한 포인터를 의미 -> record id(page id + slot Number)
- Root node와 내부 node: <pid, value>
- leaf node: <rid, value>
leaf Node
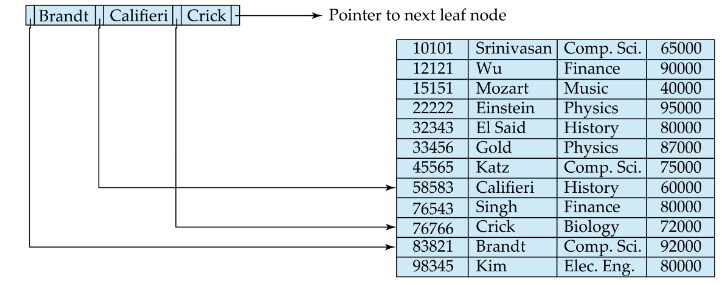
leaf node인 경우에는 (Pi,Ki)가 한 쌍을 이루고 마지막 Pn은 다음 노드를 가리킴
각 포인터는 실제 레코드의 물리적 주소를 가리킴
-> leaf node의 마지막 포인터는 형제 node를 point
- 양방향 포인트로 구현하기도 함 (오름차순 & 내림차순 search를 대비)
내부노드는 포인터에 개수 제약, 리프노드는 탐색 값에 개수 제약 그 이유는?
(노드간에 서로 다른 제약을 사용하는 이유는?)리프노드의 포인트 하나는 sibling(형제)를 연결하는데 항상 사용되므로, 포인트 개수 제한을 하면 underflow 발생 가능성
Non-leaf Node
P1 < K1
Ki-1 ≤ Pi ≤ Ki ( 2 <= i <= n-1)
(equal 관계일시 왼쪽 또는 오른쪽 한 곳에 위치(정의 상 오른쪽))
B⁺ Tree의 높이
ex1)블록 크기가 4K이고 탐색 키의 크기가 40bytes라고 가정 하면, 색인 노드에 존재하는 최대 포인터 개수(fanout 이라 고 함)는 약 100개가 되며, 100만 탐색 키를 가지는 B'-트 리 높이는 4 레벨을 가지게 된다. 그 결과 특정 데이터를 검 색하는데 4회 디스크 접근만으로 가능하다. B'-트리는 매 우 뚱뚱한 트리 모습을 가진다.
ex2)예) department 테이블에서 10000개의 레코드를 갖고, 이 중에서 dept_name 값이 '컴퓨터공학과'인 레코드를 검색할 때 인덱스가 없다면 최악의 경우 10000개의 레코드를 모두 검색해야함 , dept_name 필드에 차수가 10인 B+ tree 인덱스가 있다면!
- B+ tree의 높이 = [log10 10000] = 4
- 차수가 10, 검색 키 값의 수가 최대 10000개이므로, B+ tree의 높이는 최대 4를 넘지 않는다
- 최대 4개의 노드만 읽으며 원하는 레코드들을 찾을 수 있다
ex3)B'-트리 높이가 4이고 n=100인 경우, 최대 허용할 수 있는 탐색 키의 개수를 구하면 다음과 같다. 구하는 탐색 키의 가 수를 Y라고 하면
4 ≥ [ log(50)Y ]
관계식이 성립되며, Y=6,250,000이 된다. 6,250,000개 이 하의 탐색 키 값을 가지는 테이블에 대한 색인을 구성하여 디스크 접근 4번 만에 해당 레코드를 검색할 수 있다.
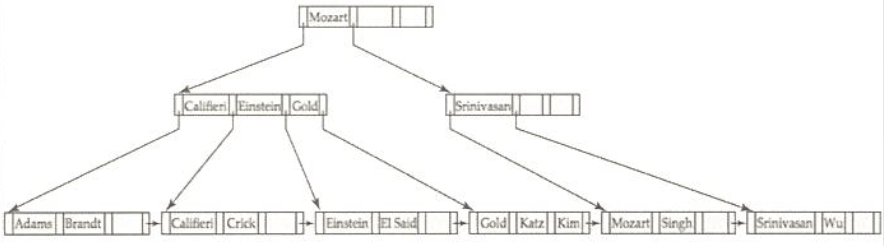
B⁺ Tree 삽입
- 삽입하려는 entry가 B⁺-트리에 존재하면:
특별한 연산이 필요 없음 (오름차순에 맞게 정렬) - 삽입하려는 entry가 B⁺-트리에 존재하지 않으면:
해당 노드를 찾아 새로운 entry를 삽입하여야 함case #1.
leaf 노드가 full 상태가 아니라면 오름차순 정렬에 맞게 삽입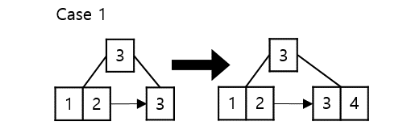
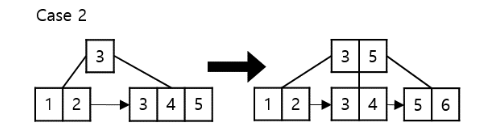
case #2.
리프 노드가 full 상태라면 노드를 분할
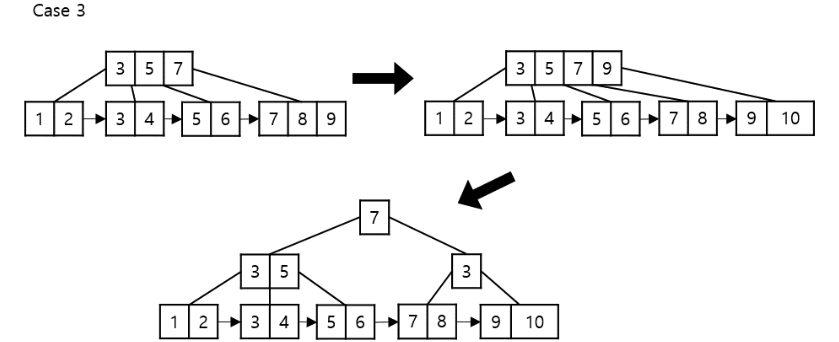
case #3.
루트가 쪼개지면 새로운 루트 노드를 생성하되 1개의 키와 2개의 양쪽 포인터로 구성되어야 하며 기존 루트 노드의 중간 key는 새로운 루트 노드에 저장한 뒤 제거
Insertion example
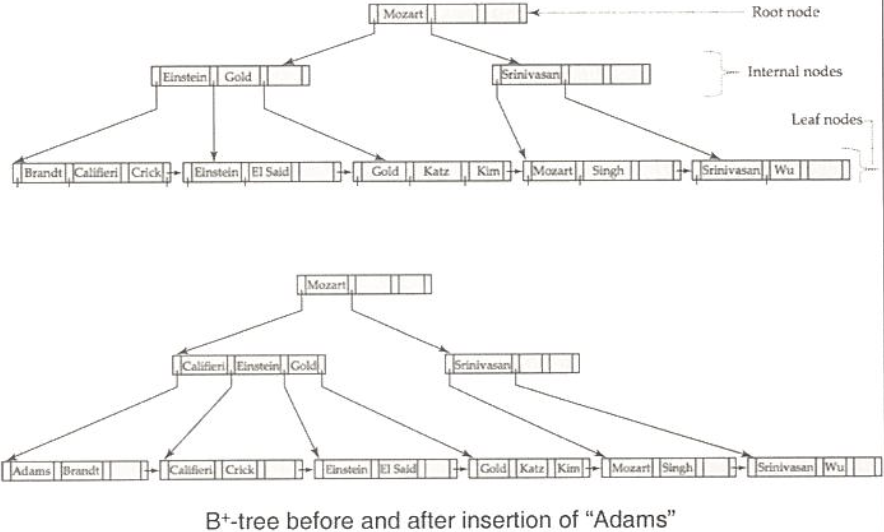
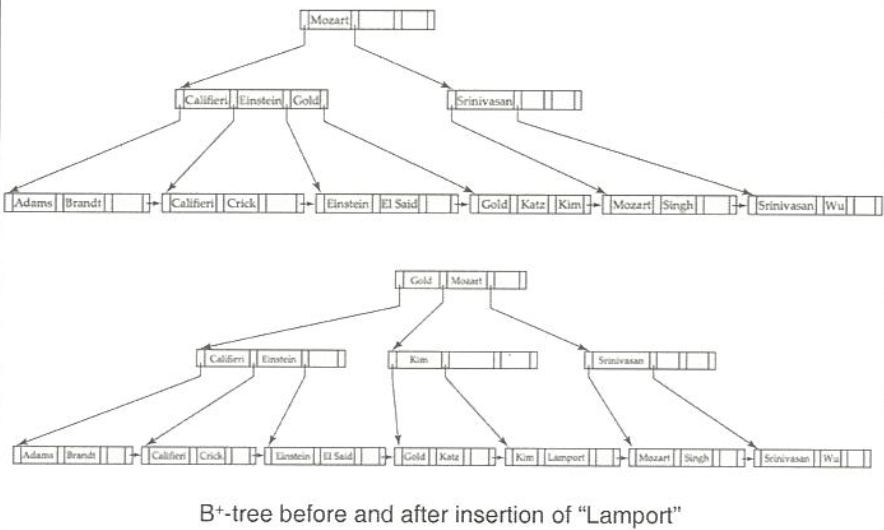
B⁺ Tree 삭제
underflow를 해결해야함: Node에 너무 적은 수의 데이터가 존재
- 옆에 존재하는 형제 Node와 병합하여 한 Node에 모든 entry가 위치할 수 있으면 형제 Node와 병합

- 병합이 가능하지 않으면(공간이 없다면) 형제 노드와 탐색 키와 포인트를 재분배

Deletion example
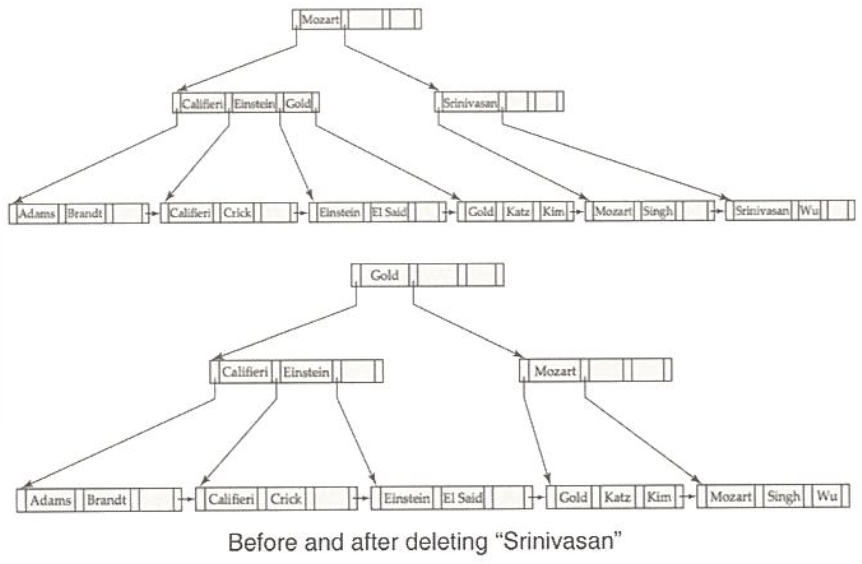
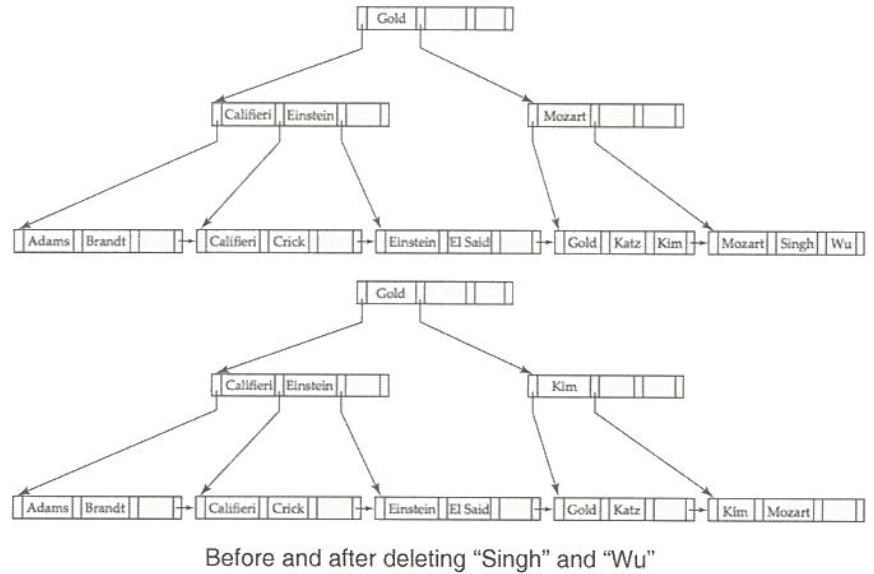
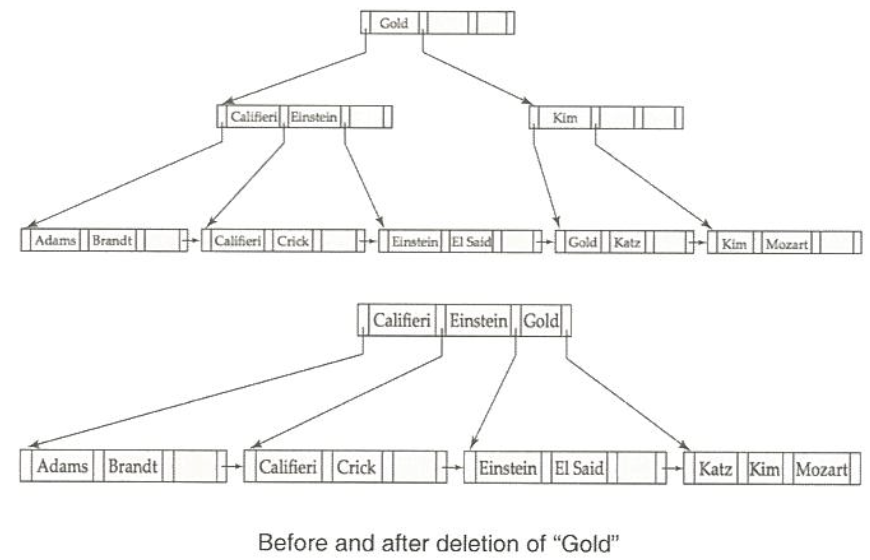 (leaf Node가 아닌 Node에는 계속적으로 남아있는 Gold)
(leaf Node가 아닌 Node에는 계속적으로 남아있는 Gold)
Non-Unique Key
비유일 탐색키: 동일 키 값을 가지는 터플이 두개 이상 존재하는 경우
(primary key가 아닌 속성에 대해 B⁺트리를 구성한 경우)
비유일 탐색키가 존재하는 경우 데이터 삭제 연산에 많은 시간 소요
- 유일한 검색 키를 가정
- RID 값을 속성에 병기하여 모든 키 값을 유일하게 함
5.3 B⁺-트리 변형
B⁺ Tree File 구성
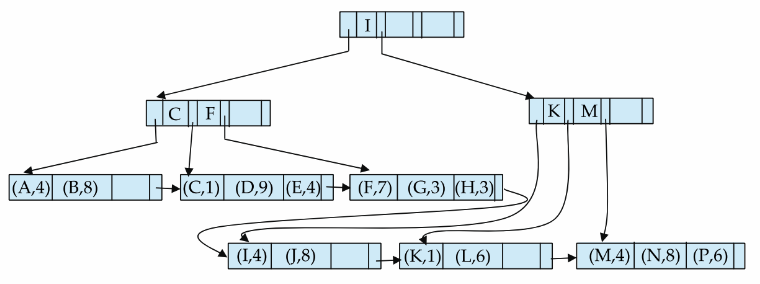
- File이 커지면서 성능이 감소하는 단점 해결
- 별도의 레코드를 저장하는 파일이 없고 leaf node에 레코드를 저장
- 삽입, 삭제를 할 때 트리가 자동으로 업데이트 되기 때문에 인덱스와 레코드 순서가 항상 같음
(해당 노드에 공간이 없으면 재분배를 하려고 함([2*n/3] 세 노드 간의 재분배)) - clustered index를 쉽게 구현 가능
Record 이동 및 Secondary Index
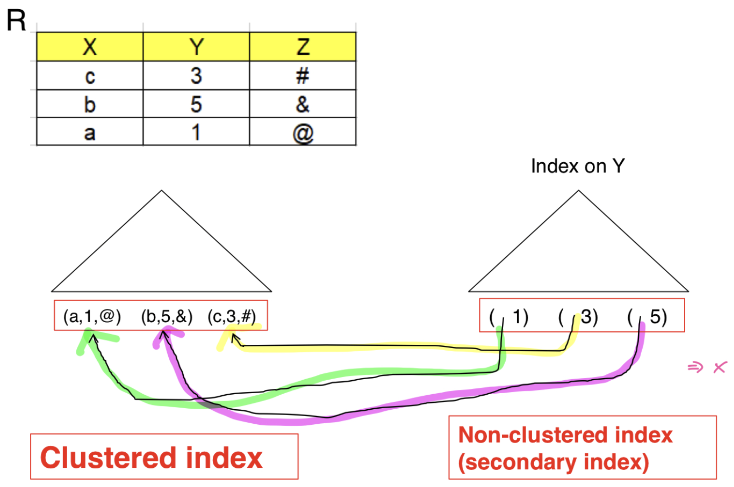
- leaf Node가 분해되어 record 위치가 변경되면 이를 참조하는 모든 색인 entry를 변경하여야함
- 레코드가 삽입, 삭제 될 때 B+ Tree file에서 레코드의 위치가 변경되기 때문에, 그럴때마다 secondary Index의 포인터 또한 갱신되어야 함
-> 오버헤드가 너무 커짐
- record에 대한 포인트 값을 저장하지 않고, 해당 record의 탐색 key(주키) 값을 저장
- secondary index에는 clustered index의 search key를 포함하고 있음
- secondary index를 이용해서 먼저 검색을 하고 clusterd index search key로 다시 한번 B+tree index file에서 조회해서 레코드를 찾음
Indexing Strings
탐색 키가 string 타입인 경우
- string의 앞부분(prefix)만 저장
-> 내부 node의 fanout 값을 높일 수 있음
Bulk Loading
Index를 구성하고 입력하게 되면 각 데이터가 입력할 때마다 색인에 새롭게 입력된 데이터를 반영하게 됨
-> 디스크 접근 횟수가 많아 비효율적
속성 데이터를 대량으로 입력할 때, 데이터 입력을 우선하고 Index를 구성
- 항목을 먼저 정렬하고 그 순서대로 삽입
- leaf level부터 tree를 레이어 별로 구성
B Tree Index
B+ Tree Index의 원형
non leaf node에도 레코드로의 포인터를 가지고 있고 Key가 중복되지 않dma
-> 탐색 키가 내부노드에 존재하지 않음
- B Tree 색인이 구현하기 어려움
- B Tree 색인이 트리 깊이가 길어질 가능성이 있음
(record 포인터 값 저장을 하기 때문)- B Tree 색인은 record를 순차적으로 검색하는 경우 트리 내부까지 검색해야 함
- B⁺ Tree 색인은 leaf Node만 검색하면 됨
B⁺ Tree이 상용 시스템에 주로 구현되어 있음
B Tree 색인은 실제로 자주 사용되지 않음
다중속성 색인
단일 속성만으로 구성되는 색인만이 존재하는 경우
특정 질의에 대해 효율적으로 대처하지 못할 수 있음
다중 색인을 적용하는 경우, 다중 색인의 처음에 나오는 속성에 대하여 exact match 형태가 적용되는 질의문에 효과적임
커버 색인
색인 entry에 탐색 키 속성 외의 다른 속성 값을 함께 저장하는 방식
특정 질의에 효과적일 수 있음
5.4 정적 해쉬 (static)
Hash function
Hash function을 이용하여 File을 구성
Hash function은 검색 키 값을 버킷 주소 값으로 변화
버킷에는 동일한 Hash function 값을 가지는 record가 위치함
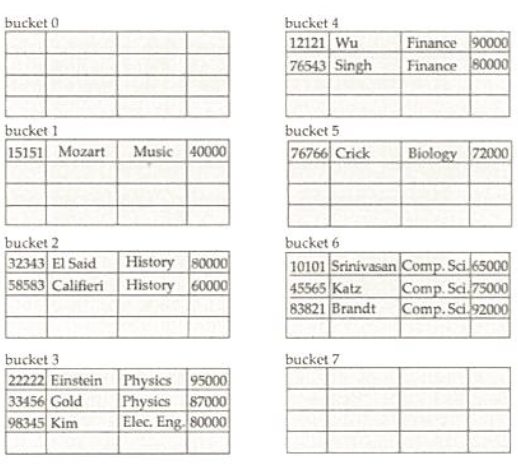
ex) Music 13(M)+21(u)+19(s)+9(i)+3(c)=65
65 mod 8 = 1 h(Music) = 1
키가 다르나 Hash값은 동일하다면 같은 bucket에 위치
Hash function은 성능을 결정하는 중요한 요소
- 균등 (uniform)
- 랜덤 (random)
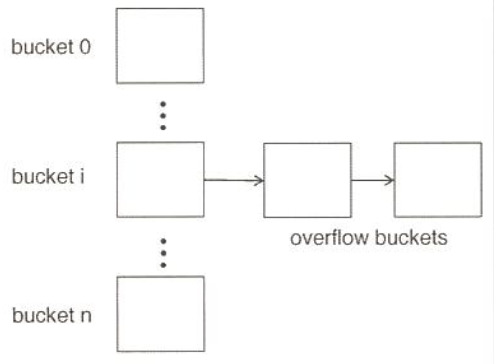
Bucket overflow
해시인덱스 혹은 해시파일의 버킷에 엔트리가 가득 찬 상황에서 해당 버킷에 엔트리가 추가되는 경우
-
Overflow chaining
가득 찬 버킷에 엔트리가 추가되어 오버플로우가 발생하면
새로운 버킷을 하나 생성하여(오버플로우 버킷) 연결 리스트로 기존 버킷과 연결 -
Open hashing
오버플로우 버킷을 새로 만들지 않고 다른 버킷의 빈자리에 엔트리를 저장하는 방법
다음순번에 저장: linear probing
재Hash하여 저장: Open hashing
(데이터베이스 환경에는 적합하지 않음(크기/시간))
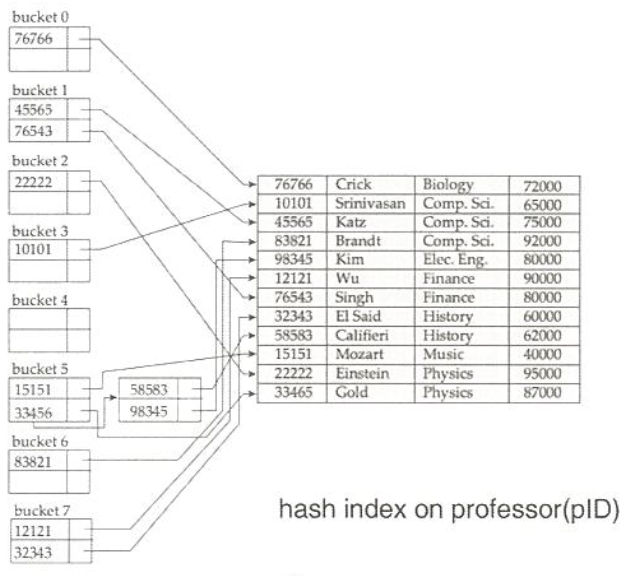
Hash Index
- Hash를 사용한 데이터 file
- 버킷에는 <탐색키, RID> 위치
-> 동일한 Hash값을 가지는 탐색키가 위치 - Secondary Index로 사용
- 데이터 File의 record 순과 Hash 버킷의 탐색키 순서는 당연히 틀림
Cons
- 해쉬 함수의 치역(range)이 항상 일정함
-> DB변화에 상관없이 항상 일정
-> DB는 데이터 량이 증가하거나 감소할 수 있는 환경임
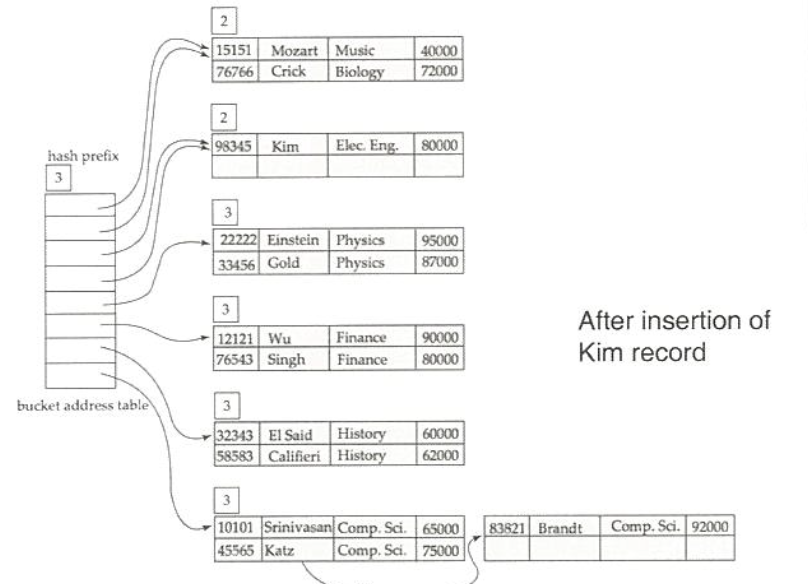
5.5 동적 해쉬 (dynamic)
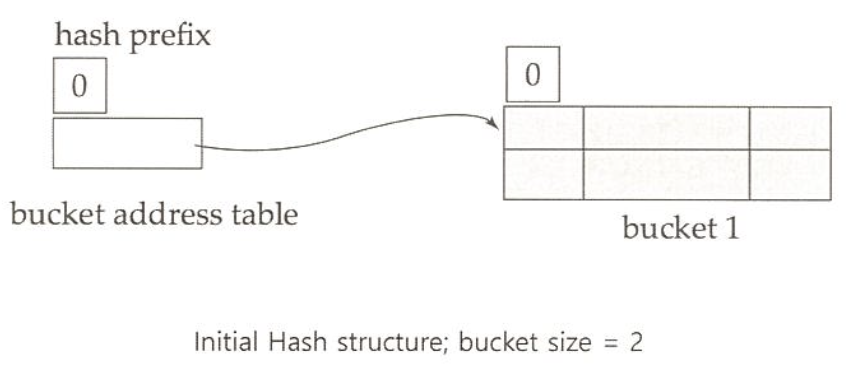
extendable hashing (확장 해쉬)
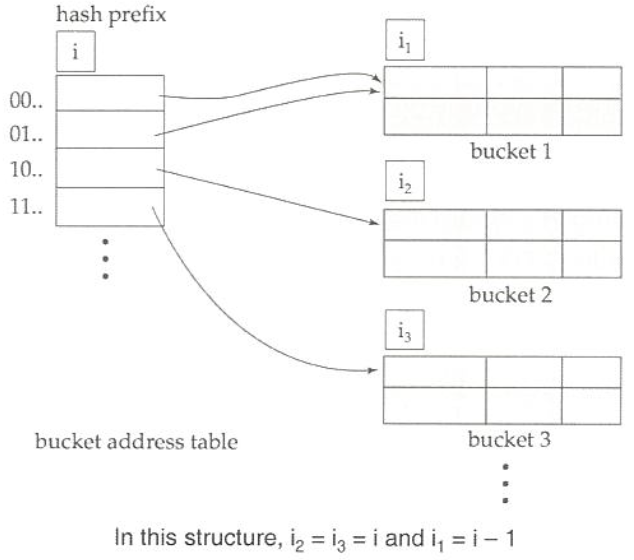
bucket address Table과 다수개의 bucket으로 운영
Hash function이 동적으로 변함
Hash prefix(해쉬 접두)값은 처음부터 몇개 bit를 사용하는가(값이 아니고 개수임)
Hash prefix의 정보는 버킷 주소 테이블과 각 버킷에 존재
탐색 역시 처음부터 Hash function 값을 통해 구한 i bit만을 참조하여 주소를 구함
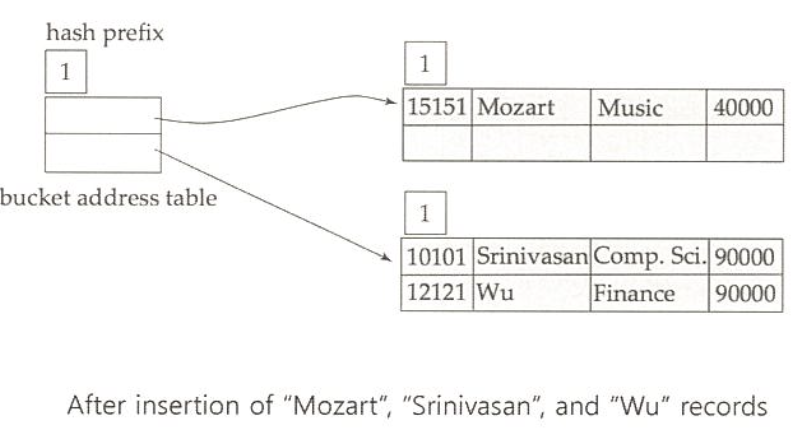
Insertion
- 해당 버킷에 공간이 있으면 record 삽입
- 해당 버킷에 공간이 없으면 버킷을 분해(split) or (overflow bucket)
버킷 분해
i = 버킷 주소 테이블 접두사 개수 / ij = 버킷 테이블 접두사 개수
- i > ij
버킷 주소 테이블의 하나 이상의 record가 동일한 버킷을 참조하는 경우
-> 버킷을 두 개의 버킷으로 확장 / 버킷 주소 테이블의 크기가 변화하진 않음
- i = ij
버킷 j를 참조하는 버킷 주소 테이블의 record가 하나만 있는 경우
-> 버킷을 두 개의 버킷으로 확장하게 되고, 버킷 주소 테이블도 2배로 확장
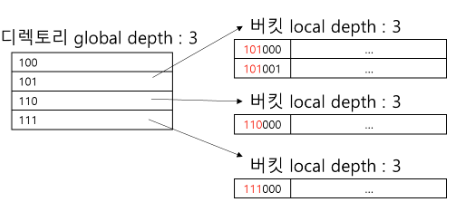
- i > ij
Deletion
삭제 후에 버킷이 빈 공간이 되면 buddy(버디) 버킷과 병합 가능
버킷 주소 테이블의 크기가 축소됨
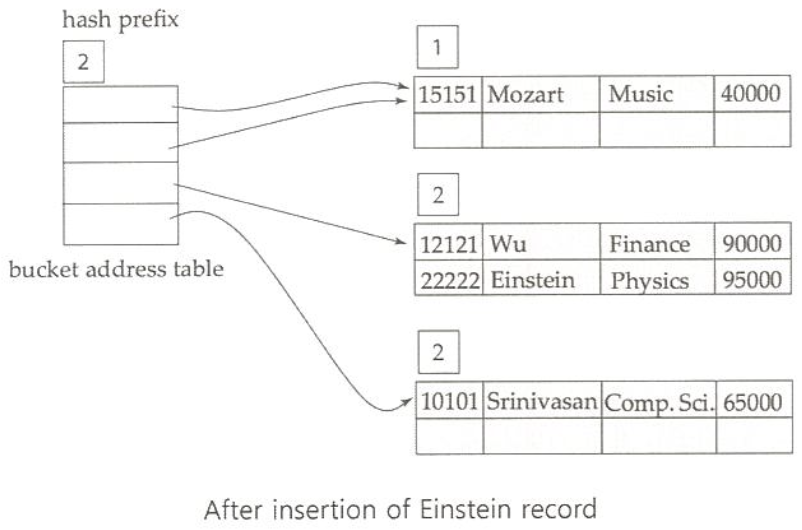
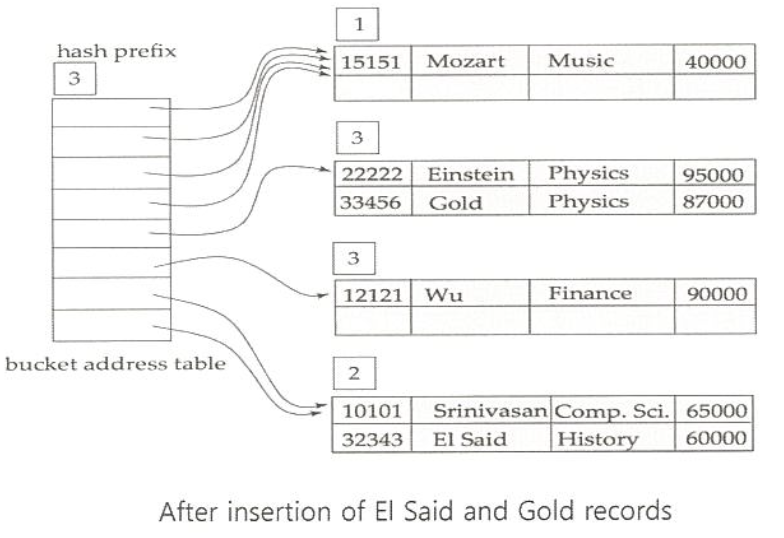
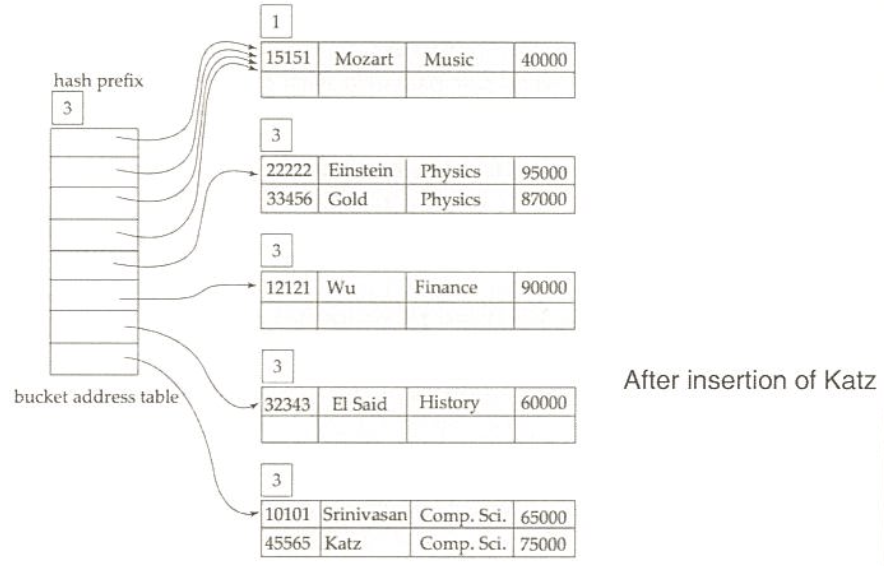
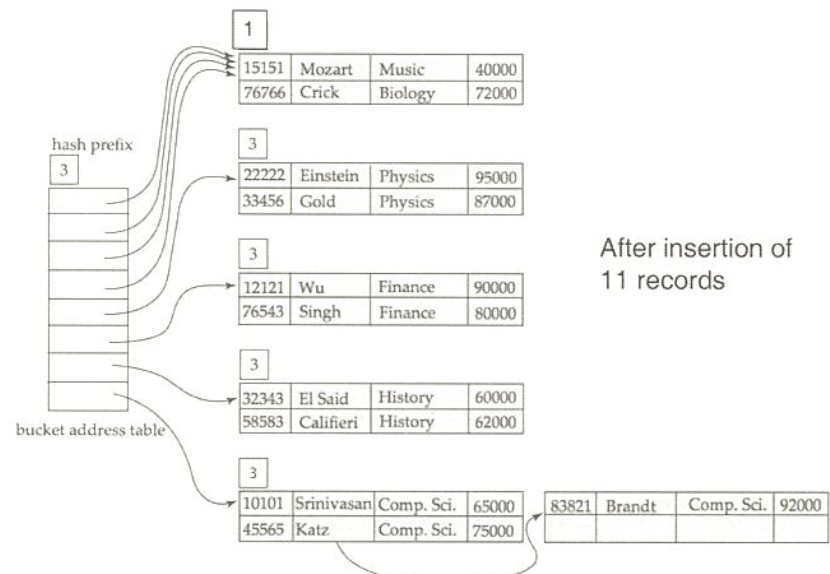
extendable hashing 예제
exact match 질의는 해쉬 또는 정렬 색인을 사용하여 빠른 질의 응답 가능
범위 질의에는 정렬 색인만이 도움됨
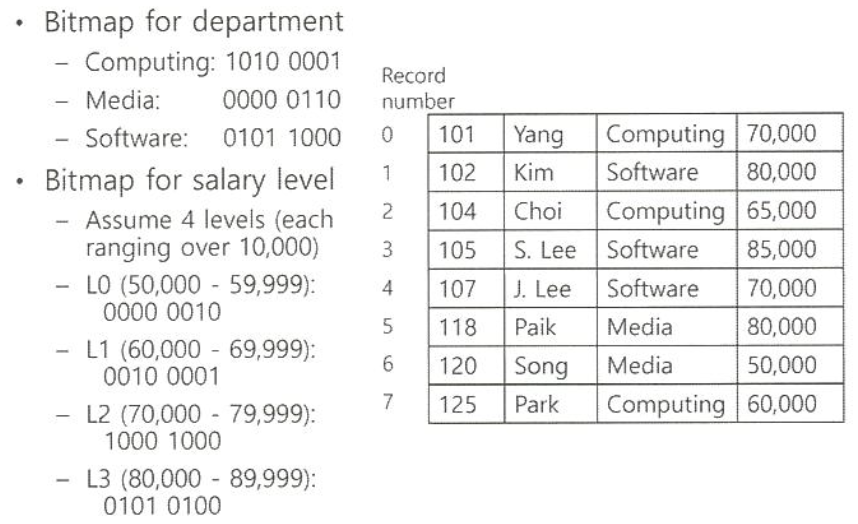
5.6 비트맵 색인
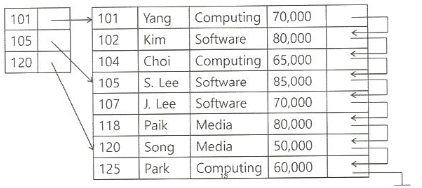
Bitmap Indices
- 다중 키 질의에 효율적
- 탐색키가 많지 않은 값에 적합 (남/여, 1-4학년)
- record 번호를 이용한 record 탐색이 가능하고 용이하여야 함
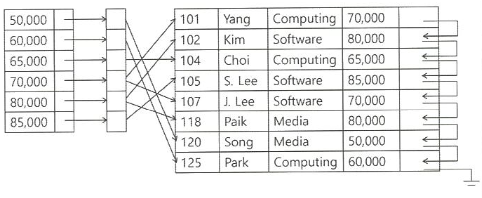
ex) bitmap for gender / 수입 level
비트연산을 통해 다중 속성에 대한 질의를 효율적으로 처리할 수 있음
- intersection (and)
- union (or)
- complementation (not)
공간 오버헤드
색인에 의한 공간 오버헤드가 1% 일 정도로 효율적이고 연산이 빠름
ex) 32bit 컴퓨터 기계
- 1,000,000 bits = 125 Kbytes
- 125 Kbyte / 4 byte = 32,000 instructions
Deletion & Null 값
삭제된 빈 공간을 채우지 않음
-> 기존 터플에 할당된 번호에 변화가 생기는 비효율성
-> 존재비트맵을 통해 존재비트맵의 i가 0이면 record가 존재하지 않는 것
-> 질의 결과에서 존재비트맵과 중간 결과 비트맵과 and 연산하여 수행
NULL값이 허용된다면 이를 구분하기 위해 NULL값 비트맵을 유지
(NULL의 bit값은 1)
-> 질의 결과에서 NULL값 비트맵과 중간 결과 비트맵을 complement와 and 연산하여 수행
SQL 색인 선언
- 표준 SQL은 색인 선언에 대한 규약이 없음
- 상용 DB 시스템은 자체적으로 색인 생성/삭제를 지원