99클럽 코테 스터디 11일차 DFS(깊이 우선 탐색)

Seongbin·2024년 11월 8일

99클럽 DFS TIL 개발자취업 깊이 우선 탐색 코딩테스트준비 항해99

99클럽 코테 스터디

목록 보기

11/24

오늘의 학습 키워드

DFS, Depth-First Search(깊이 우선 탐색)

그래프 탐색이란?

하나의 정점으로부터 시작하여 차례대로 모든 정점들을 한 번씩 방문하는 것

Ex) 특정 도시에서 다른 도시로 갈 수 있는지 없는지, 전자 회로에서 특정 단자와 단자가 서로 연결되어 있는지

그러면 DFS란?
루트 노드(혹은 다른 임의의 노드)에서 시작해서 다음 분기(branch)로 넘어가기 전에 해당 분기를 완벽하게 탐색하는 방법

미로를 탐색할 때 한 방향으로 갈 수 있을 때까지 계속 가다가 더 이상 갈 수 없게 되면 다시 가장 가까운 갈림길로 돌아와서 이곳으로부터 다른 방향으로 다시 탐색을 진행하는 방법과 유사하다.
즉, 넓게(wide) 탐색하기 전에 깊게(deep) 탐색하는 것이다.
사용하는 경우: 모든 노드를 방문 하고자 하는 경우에 이 방법을 선택한다.
깊이 우선 탐색(DFS)이 너비 우선 탐색(BFS)보다 좀 더 간단하다.
단순 검색 속도 자체는 너비 우선 탐색(BFS)에 비해서 느리다.

깊이 우선 탐색(DFS)의 특징

자기 자신을 호출하는 순환 알고리즘의 형태 를 가지고 있다.
이 알고리즘을 구현할 때 가장 큰 차이점은, 그래프 탐색의 경우 어떤 노드를 방문했었는지 여부를 반드시 검사 해야 한다는 것이다.이를 검사하지 않으면 무한 루프에 빠질 수도 있다.
찾고자하는 답이 트리에서부터 멀어질 수록 DFS가 유리하다. (BFS에 비해)

오늘의 문제

백준 25195번

https://www.acmicpc.net/problem/25195

문제 설명

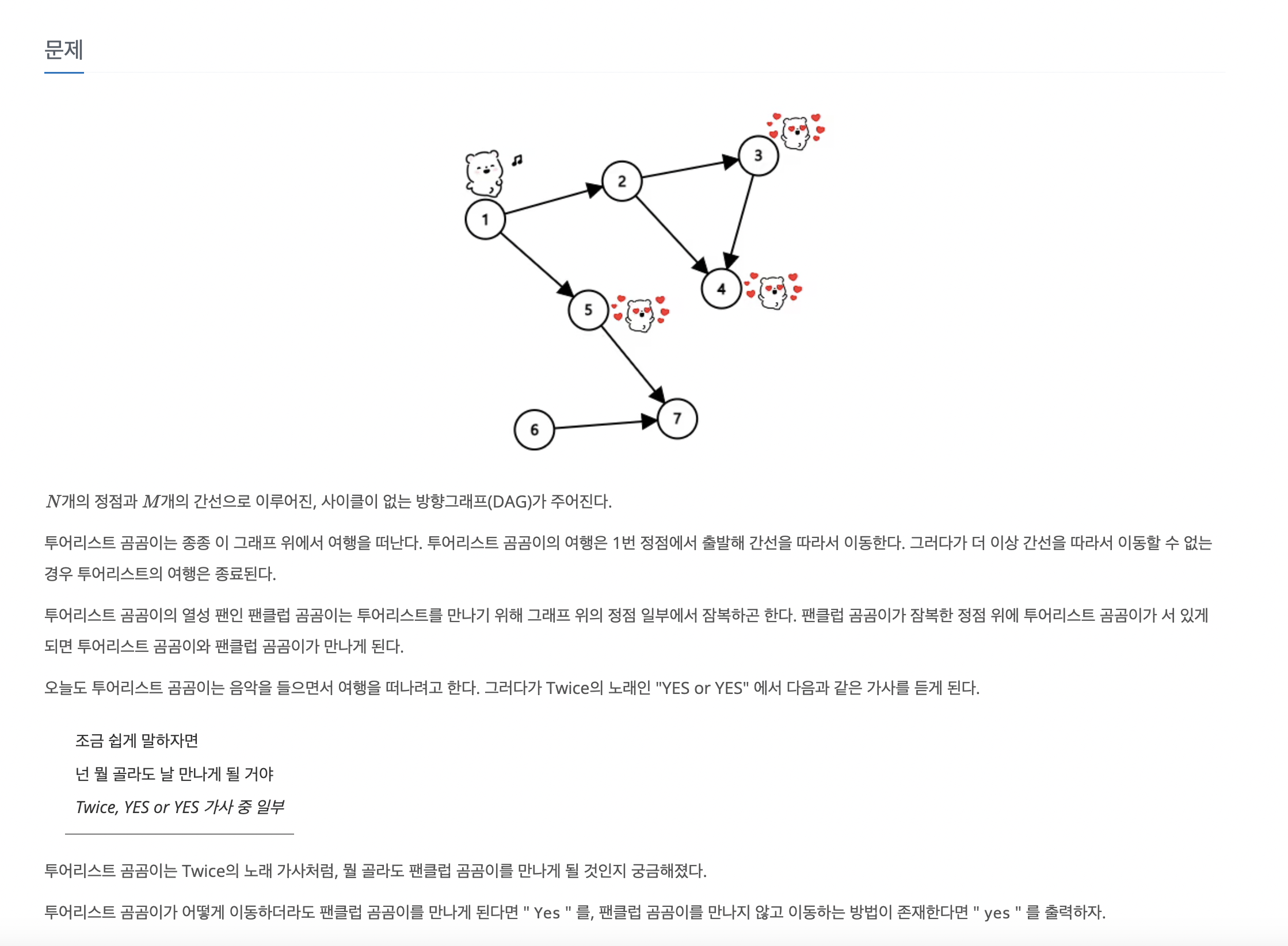
입출력 예

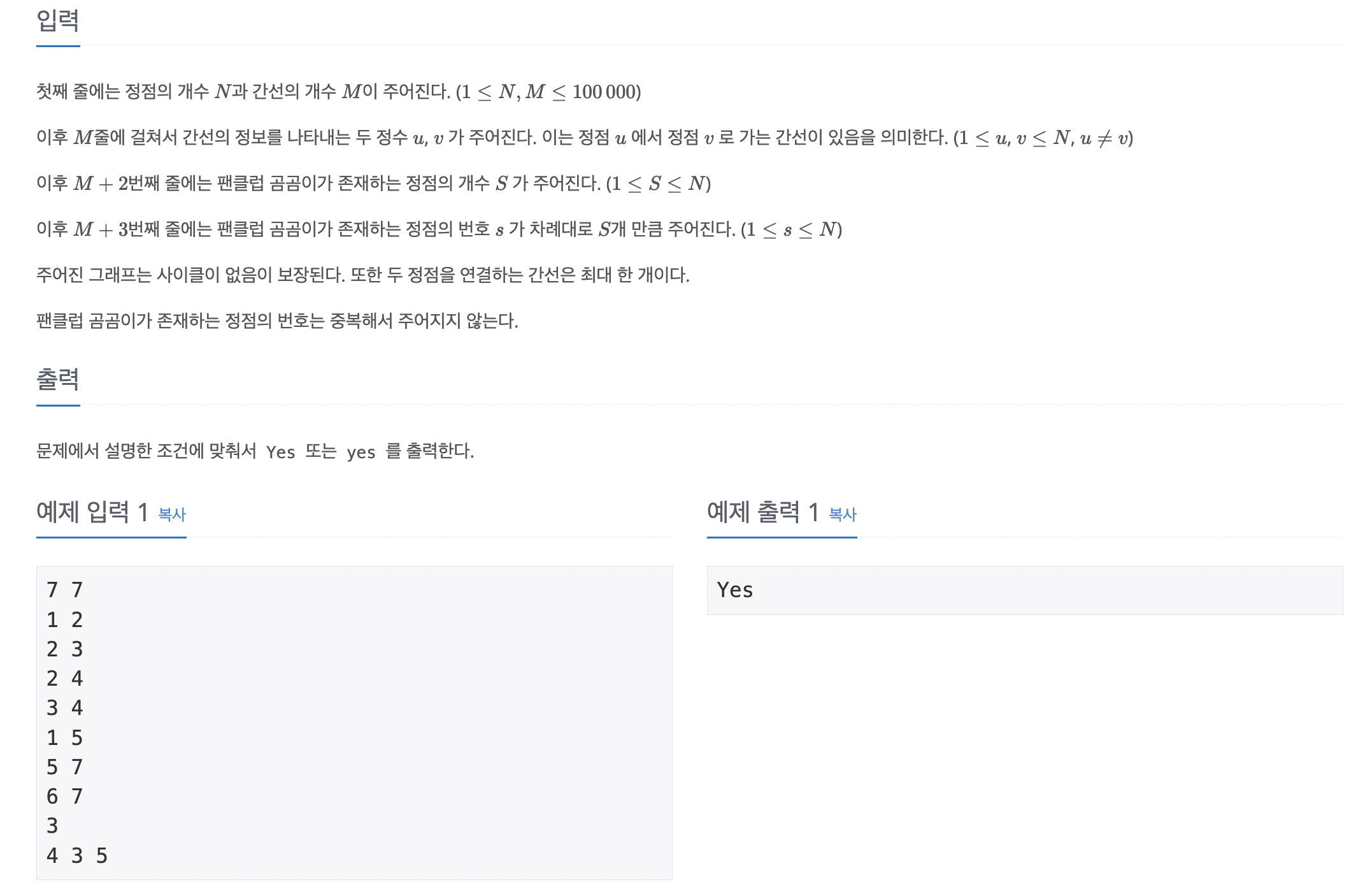
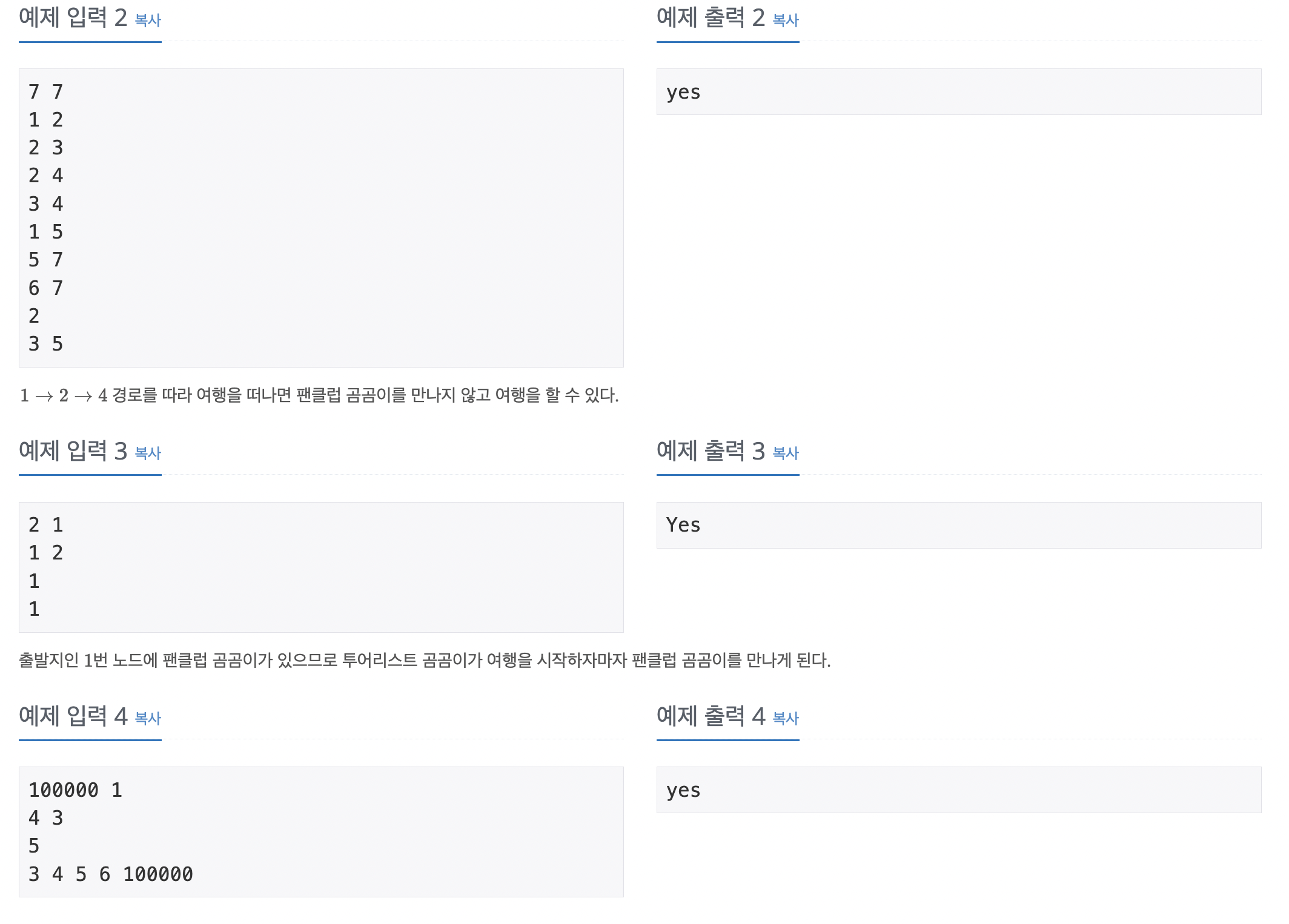
문제 생각해보기

곰곰이는 팬들이 있다.

그리고 곰곰이는 간선(양방향 아님)을 통해 팬미팅?을 하는데 투어를 하면서 곰곰이 팬들을 만나지 못하면 yes를

팬들과 만난다면 Yes를 출력하면 된다.
Yes인 상황은 예시 그림에서 잘 설명해주었고
yes인 상황은 다음과 같다.

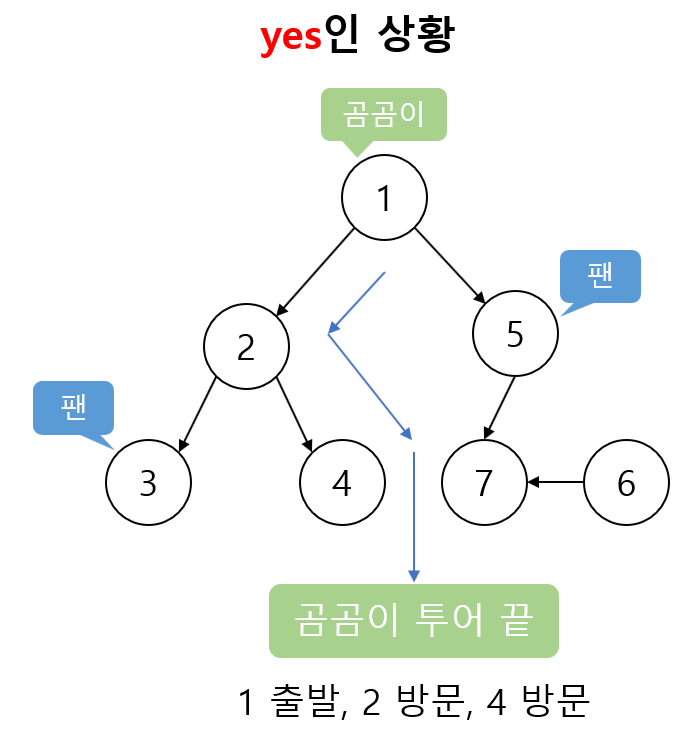
출처:https://9hyuk9.tistory.com/51

DFS 탐색 순서 (입출력 예시 1 적용)

시작 도시: 출발 도시 1에서 DFS 탐색을 시작한다. 출발 도시를 방문 처리하며, 방문 여부를 기록한다.
첫 번째 단계: 도시 1에서 갈 수 있는 모든 인접 도시를 탐색한다. 도시 1은 도시 2와 5로 연결되어 있다. DFS는 먼저 도시 2로 이동하여 탐색을 진행한다.
두 번째 단계: 도시 2에서 인접한 도시들을 탐색한다. 도시 2는 도시 3과 4로 연결되어 있다. DFS는 도시 3으로 이동한다.
세 번째 단계: 도시 3에서 인접한 도시인 4로 이동한다. 이때, 도시 4에 팬클럽 곰곰이가 존재하므로 방문 처리가 된다.
다시 도시 2로 백트래킹: 도시 2에서 아직 방문하지 않은 도시 4로 이동하지만, 이미 방문한 상태이므로 더 이상 진행하지 않는다. 이후 도시 1로 백트래킹한다.
도시 5 탐색: 도시 1에서 아직 방문하지 않은 도시 5로 이동한다. 도시 5에는 팬클럽 곰곰이가 존재하므로 방문 처리가 된다. 이후 도시 7로 이동하며, 방문을 완료한다.

따라서 DFS 탐색 순서는 1 -> 2 -> 3 -> 4 -> 5 -> 7이며, 모든 경로에서 팬클럽 곰곰이를 만나게 된다. 결과는 "Yes"이다.

1. 기본 설정 및 입력 처리

import sys
input = sys.stdin.readline
sys.setrecursionlimit(10**7)

n, m = map(int, input().split())
graph = [[] for _ in range(n+1)]

import sys와 sys.setrecursionlimit(10**7) : 파이썬의 재귀 한도를 늘리기 위해 사용한다. DFS의 깊이가 매우 깊어질 수 있으므로 설정한다.
n, m = map(int, input().split()) : 정점의 개수 n과 간선의 개수 m을 입력받는다.
graph = [[] for _ in range(n+1)] : 각 정점 간의 단방향 간선을 인접 리스트로 표현하기 위한 그래프를 초기화한다.

2. 그래프 구성

for _ in range(m):
    u, v = map(int, input().split())
    graph[u].append(v)

for _ in range(m) : m개의 간선 정보를 입력받아 그래프를 구성한다.
u, v = map(int, input().split()) : 정점 u에서 정점 v로 가는 단방향 간선이 존재한다는 의미이다.
graph[u].append(v) : 정점 u의 인접 리스트에 정점 v를 추가하여 단방향 간선을 표현한다.

3. 팬클럽 곰곰이 위치 설정

visited = [False for _ in range(n+1)]
s = int(input())

for x in list(map(int, input().split())):
    visited[x] = True

visited = [False for _ in range(n+1)] : 각 도시의 방문 여부를 기록하는 리스트를 초기화한다.
s = int(input()) : 팬클럽 곰곰이가 존재하는 정점의 개수를 입력받는다.
for x in list(map(int, input().split())) : 팬클럽 곰곰이가 존재하는 정점의 번호를 입력받아 해당 정점을 방문 처리한다.

4. DFS 탐색 정의 및 초기화

def dfs(s):
    visited[s] = True
    is_meet = not bool(graph[s])
    for u in graph[s]:
        if not visited[u] and dfs(u):
            return True
    return is_meet

def dfs(s) : 시작 정점 s에서 DFS 탐색을 수행하는 함수이다.
visited[s] = True : 현재 정점을 방문 처리한다.
is_meet = not bool(graph[s]) : 현재 정점에서 더 이상 갈 수 있는 경로가 없는지를 확인하여 팬클럽을 만났는지 여부를 기록한다.
for u in graph[s] : 현재 정점과 연결된 모든 인접 정점을 탐색한다.
if not visited[u] and dfs(u) : 아직 방문하지 않은 인접 정점에 대해 재귀적으로 DFS를 수행하며 팬클럽을 만났는지 확인한다.
return is_meet : 팬클럽을 만났다면 True를 반환한다.

5. 결과 출력

print("Yes" if visited[1] or not dfs(1) else "yes")

출발지인 1번 정점에서 시작하여 팬클럽을 만나는 모든 경우를 확인한 후, 조건에 따라 "Yes" 또는 "yes"를 출력한다.

전체 풀이

import sys
input = sys.stdin.readline
sys.setrecursionlimit(10**7)

n, m = map(int, input().split())
graph = [[] for _ in range(n+1)]
for _ in range(m):
    u, v = map(int, input().split())
    graph[u].append(v)
visited = [False for _ in range(n+1)]
s = int(input())

for x in list(map(int, input().split())):
    visited[x] = True

def dfs(s):
    visited[s] = True
    is_meet = not bool(graph[s])
    for u in graph[s]:
        if not visited[u] and dfs(u):
            return True
    return is_meet
    
print("Yes" if visited[1] or not dfs(1) else "yes")