
오늘의 학습 키워드
GREEDY 욕심쟁이!
그리디란?
- 최적의 값을 구해야 하는 상황에서 사용되는 근시안적인 방법론으로 ‘각 단계에서 최적이라고 생각되는 것을 선택’ 해 나가는 방식으로 진행하여 최종적인 해답에 도달하는 알고리즘이다.
- 이때, 항상 최적의 값을 보장하는것이 아니라 최적의 값의 ‘근사한 값’을 목표로 하고 있다.
- 주로 문제를 분할 가능한 문제들로 분할한 뒤, 각 문제들에 대한 최적해를 구한 뒤 이를 결합하여 전체 문제의 최적해를 구하는 경우에 주로 사용된다.
오늘의 문제
백준 2847번
https://www.acmicpc.net/problem/2847

입출력
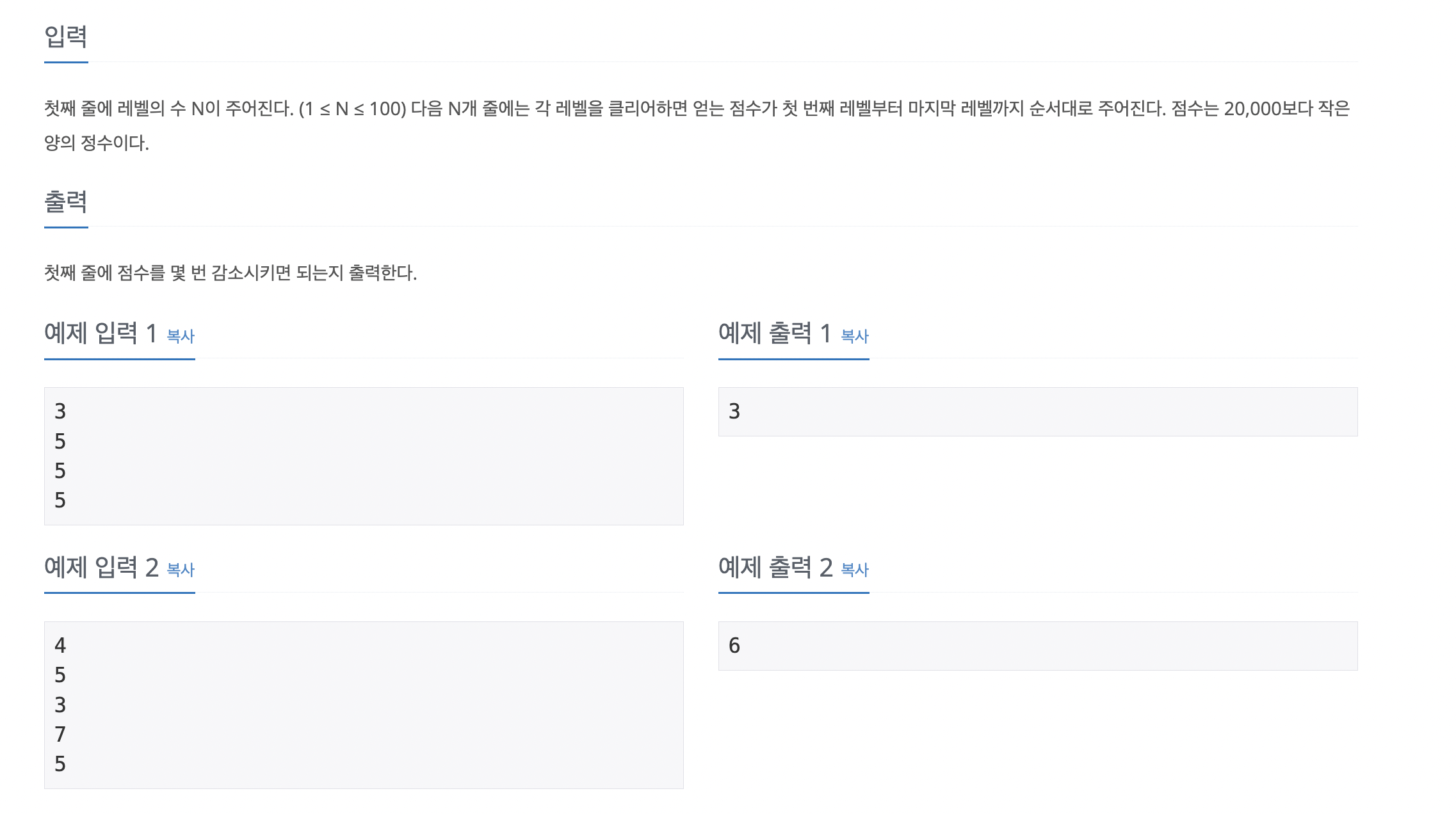
문제 접근해보기
이 문제는 각 레벨의 점수가 난이도 순으로 증가하도록 만들어야 한다. 즉, 높은 레벨일수록 더 높은 점수를 가져야 하므로, 만약 다음 레벨의 점수가 현재 레벨의 점수보다 작거나 같다면, 그 점수를 줄여야 한다. 이때, 점수를 줄이는 횟수를 최소화하는 것이 목표이다.
그리디 알고리즘은 매 순간 최적의 선택을 반복하여 전체 문제를 해결하는 방식이다. 이 문제에서는 점수를 뒤에서부터 탐색하면서, 현재 레벨의 점수가 다음 레벨의 점수보다 작도록 점수를 조정하는 방식으로 문제를 해결한다.
1. 기본 설정 및 입력 처리
n = int(input())
score = []
cnt = 0
for _ in range(n):
score.append(int(input()))-
n = int(input()): 레벨의 수를 입력받는다. -
score = []: 각 레벨의 점수를 저장할 리스트를 초기화한다. -
cnt = 0: 점수를 줄인 횟수를 저장할 변수를 초기화한다. -
for _ in range(n): 각 레벨의 점수를 입력받아 score 리스트에 추가한다.
2. 점수 조정 반복문
for i in range(n - 1, 0, -1):
if score[i] <= score[i - 1]:
cnt += (score[i - 1] - score[i] + 1)
score[i - 1] = score[i] - 1-
for i in range(n - 1, 0, -1): 뒤에서부터 두 번째 레벨부터 첫 번째 레벨까지 탐색. -
if score[i] <= score[i - 1]: 현재 레벨의 점수가 다음 레벨의 점수보다 크거나 같은 경우 점수를 조정. -
cnt += (score[i - 1] - score[i] + 1): 점수를 줄이는 횟수를 계산하여 cnt에 더해준다. -
score[i - 1] = score[i] - 1: 다음 레벨의 점수가 현재 레벨보다 작도록 설정.
3. 결과 출력
print(cnt): 점수를 줄인 총 횟수를 출력
그리디 적용해보기 (입력 예제1 적용)
-
초기 상태: score = [5, 5, 5]
-
첫 번째 반복 (i = 2): score2가 score1보다 작거나 같으므로, score[1]을 4로 줄이고 cnt += 1 (현재 cnt = 1)
-
두 번째 반복 (i = 1): score1가 score0보다 작거나 같으므로, score[0]을 3으로 줄이고 cnt += 2 (현재 cnt = 3)
-
최종 결과: cnt = 3
왜 그리디로 풀까?
-
매 순간 현재 레벨의 점수가 다음 레벨보다 높거나 같은 경우 최소한으로 줄이는 선택을 반복하여, 전체적으로 점수가 증가하는 순서로 만들기 위해 그리디 접근을 사용한다.
-
각 레벨을 뒤에서부터 탐색하면서 필요한 최소한의 조정을 하는 것이 전체적으로 가장 적은 조정 횟수를 보장하기 때문에 그리디 방법이 적합하다.
전체 풀이
n = int(input())
score = []
cnt = 0
for _ in range(n):
score.append(int(input()))
for i in range(n - 1, 0, -1):
if score[i] <= score[i - 1]:
cnt += (score[i - 1] - score[i] + 1)
score[i - 1] = score[i] - 1
print(cnt)오늘의 회고
🔥 뒤 점수에 -1을 적용하는 방법은 생각했지만 코드에 적용을 하지 못해서 찾아보고 풀 수 있었다.
