
오늘의 학습 키워드
GREEDY 욕심쟁이!
그리디란?
- 최적의 값을 구해야 하는 상황에서 사용되는 근시안적인 방법론으로 ‘각 단계에서 최적이라고 생각되는 것을 선택’ 해 나가는 방식으로 진행하여 최종적인 해답에 도달하는 알고리즘이다.
- 이때, 항상 최적의 값을 보장하는것이 아니라 최적의 값의 ‘근사한 값’을 목표로 하고 있다.
- 주로 문제를 분할 가능한 문제들로 분할한 뒤, 각 문제들에 대한 최적해를 구한 뒤 이를 결합하여 전체 문제의 최적해를 구하는 경우에 주로 사용된다.
오늘의 문제
백준 2212번
https://www.acmicpc.net/problem/2212

입출력
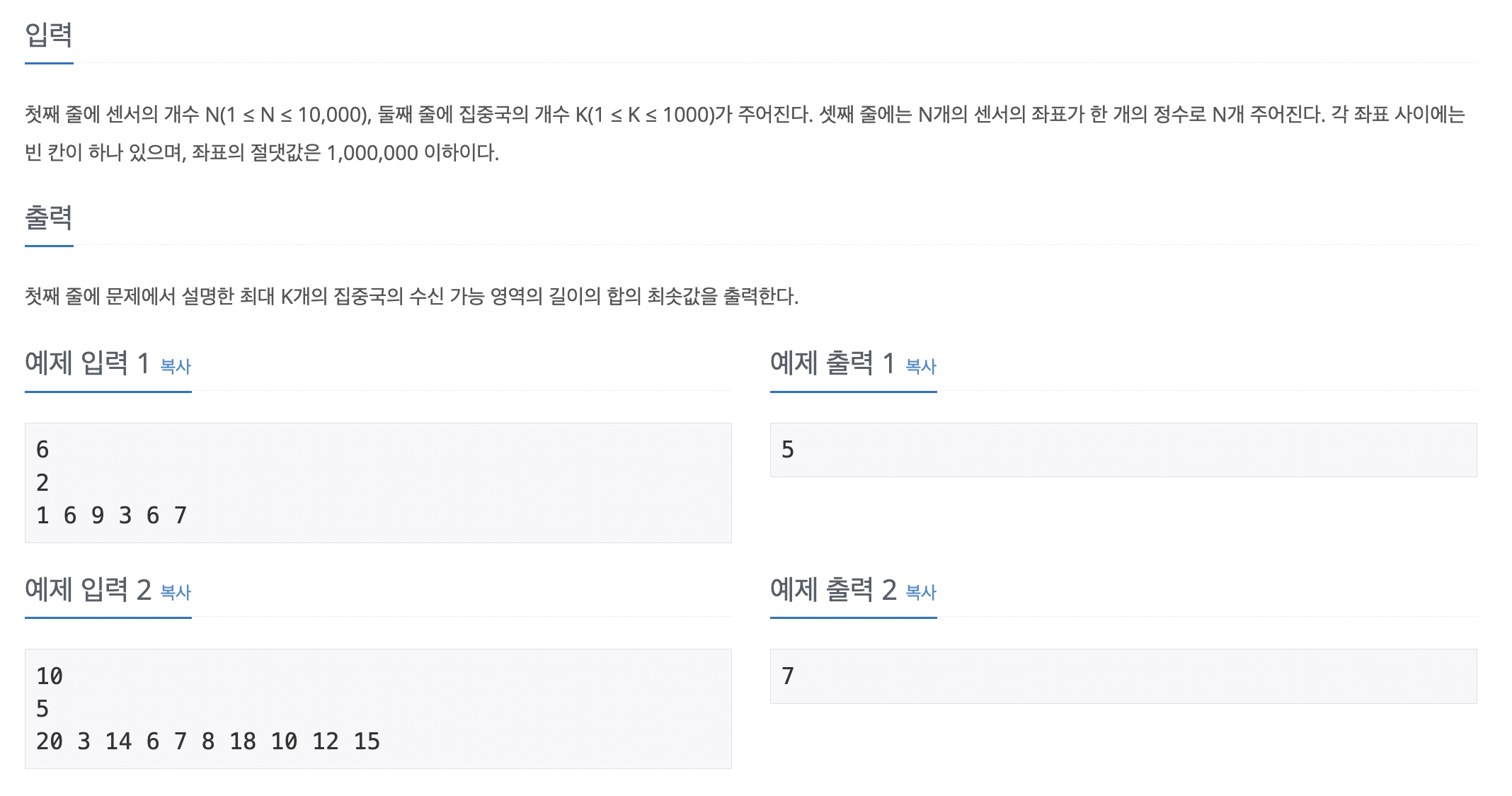
문제 접근해보기
- 이 문제는 고속도로 위에 설치된 N개의 센서를 통해 수집된 자료를 몇 개의 집중국을 통해 분석하고자 하는 문제이다. K개의 집중국을 설치할 수 있으며, 모든 센서들이 적어도 하나의 집중국과 연결되어야 한다. 이때, 집중국의 수신 가능 영역의 길이의 합을 최소화하는 것이 목표이다.
- 고속도로는 직선으로 간주되며, 각 센서의 위치는 정수로 표현된다. 이 문제는 그리디 알고리즘을 사용하여 집중국의 수신 가능 영역의 길이의 최소합을 구하는 문제이다.
- 이 문제는 정렬과 그리디 알고리즘을 사용하여 센서 간의 거리를 최소화하는 문제이다.
- 센서 간의 거리를 계산한 후, 가장 긴 거리부터 차례로 끊어내어 집중국을 배치하는 것이 최적의 해법이다.
1. 기본 설정 및 정렬
n = int(input())
k = int(input())
sensor = list(map(int,input().split()))
sensor.sort()- n은 센서의 개수, k는 집중국의 개수를 입력는다.
- sensor 리스트에 센서의 좌표를 입력받은 후, 오름차순으로 정렬한다. 정렬하는 이유는 거리 계산을 위해 센서들이 직선 상에 순서대로 놓여있어야 하기 때문이다.
2. 센서 간 거리 계산
array = []
for i in range(0,n-1):
array.append(sensor[i+1] - sensor[i])array.append(sensor[i + 1] - sensor[i]): 각 센서 간의 거리 계산하여 리스트에 저장하고 array 리스트에 저장- 예를 들어, 정렬된 센서의 좌표가 [1, 3, 6, 7, 9]라면 센서 간의 거리는 [2, 3, 1, 2]가 됩니다.
- 이 거리들은 집중국 설치 시 고려해야 할 간격들이다.
3. 거리 정렬 및 최소 거리 계산:
array.sort()
print(sum(array[:n-k]))- 센서 간 거리 리스트 array를 오름차순으로 정렬. 이 작업은 가장 긴 거리를 끊어내어 집중국이 연결되지 않아도 되는 곳으로 만들기 위해 필요.
- 집중국의 개수가 k개이기 때문에, k개의 집중국이 있을 경우 k-1개의 거리를 끊어내면 됨.
- 최종적으로 최소 거리를 계산하기 위해 sum(array[:n - k])를 계산. 이는 n - k개의 거리를 더하는 작업으로, 집중국을 최대한 효율적으로 배치한 후의 총 거리의 합을 구하는 것.
그리디 적용해보기 (입력 예제1 적용)
- 입력 처리 및 정렬:
- 센서 개수 n = 6, 집중국 개수 k = 2.
- 센서 좌표 [1, 6, 9, 3, 6, 7]을 입력받고 정렬하여 [1, 3, 6, 6, 7, 9]로 변환.
- 센서 간 거리 계산:
- 정렬된 센서들 간의 거리 계산:
3 - 1 = 2
6 - 3 = 3
6 - 6 = 0
7 - 6 = 1
9 - 7 = 2 - 거리 리스트 array = [2, 3, 0, 1, 2].
- 거리 정렬 및 최소 거리 계산:
- 거리 리스트를 정렬하여 array = [0, 1, 2, 2, 3].
- n - k = 6 - 2 = 4. 즉, 거리 리스트에서 최소합을 구할 때 4개의 거리를 더함.
- sum(array[:4]) = 0 + 1 + 2 + 2 = 5.
왜 그리디로 풀까?
-
이 문제는 그리디 알고리즘을 통해 해결할 수 있다. 그리디 알고리즘은 각 단계에서 가장 최적의 선택을 반복하여 전체 문제의 최적의 해를 찾는 방법.
-
이 문제에서는 각 센서 간의 거리를 오름차순으로 정렬하고, 가장 긴 거리를 끊어내는 방식으로 집중국을 배치하는 것이 최적의 선택.
-
집중국이 많을수록 센서 간의 거리 합이 줄어들기 때문에, 가장 큰 거리를 끊어내어 집중국을 배치하는 것이 전체 거리의 합을 최소화하는 방법.
전체 풀이
import sys
input = sys.stdin.readline
n = int(input())
k = int(input())
sensor = list(map(int,input().split()))
sensor.sort()
array = []
for i in range(0,n-1):
array.append(sensor[i+1] - sensor[i])
array.sort()
print(sum(array[:n-k]))오늘의 회고
🔥 그리디로 푸는 것은 여전히 헷갈린다 복습해봐야겠다.
