99클럽 코테 스터디 2일차 이분 탐색/ 이진 탐색 with. 등차수열

오늘의 학습 키워드

이분 탐색/이진 탐색(Binary Search) with 등차수열

이분 탐색(이진 탐색)이란?

• 정렬되어 있는 리스트에서 탐색 범위를 타노스처럼 절반씩 좁혀가며 데이터를 탐색하는 방법이다.
• 탐색 기법중 하나로, 탐색하고 싶은 범위를 두 부분으로 분할해서 찾는 방법이다.
• 두 부분으로 계속 분할해서 조건에 맞는지 찾아가기 때문에, 시간 복잡도가 O(log n)으로 매우 빠른편
  

등차 수열이란?

• 연속된 두 항의 차이가 일정한 수열이다.( 두 항의 차이: 공차(d) )
• ex)
  • 수열 A: 5, 7, 9, 11, . . . -> 공차(d)는 2
  • 수열 B: 6, 1,-4, 9, . . . -> 공차(d)는 -5

버블티 좀 땡긴다..? 등갈비도..
공차~ 등차~ 영차~ 내 목표는 좋은 집, 차~

---

오늘의 문제

백준 11561번

https://www.acmicpc.net/problem/11561
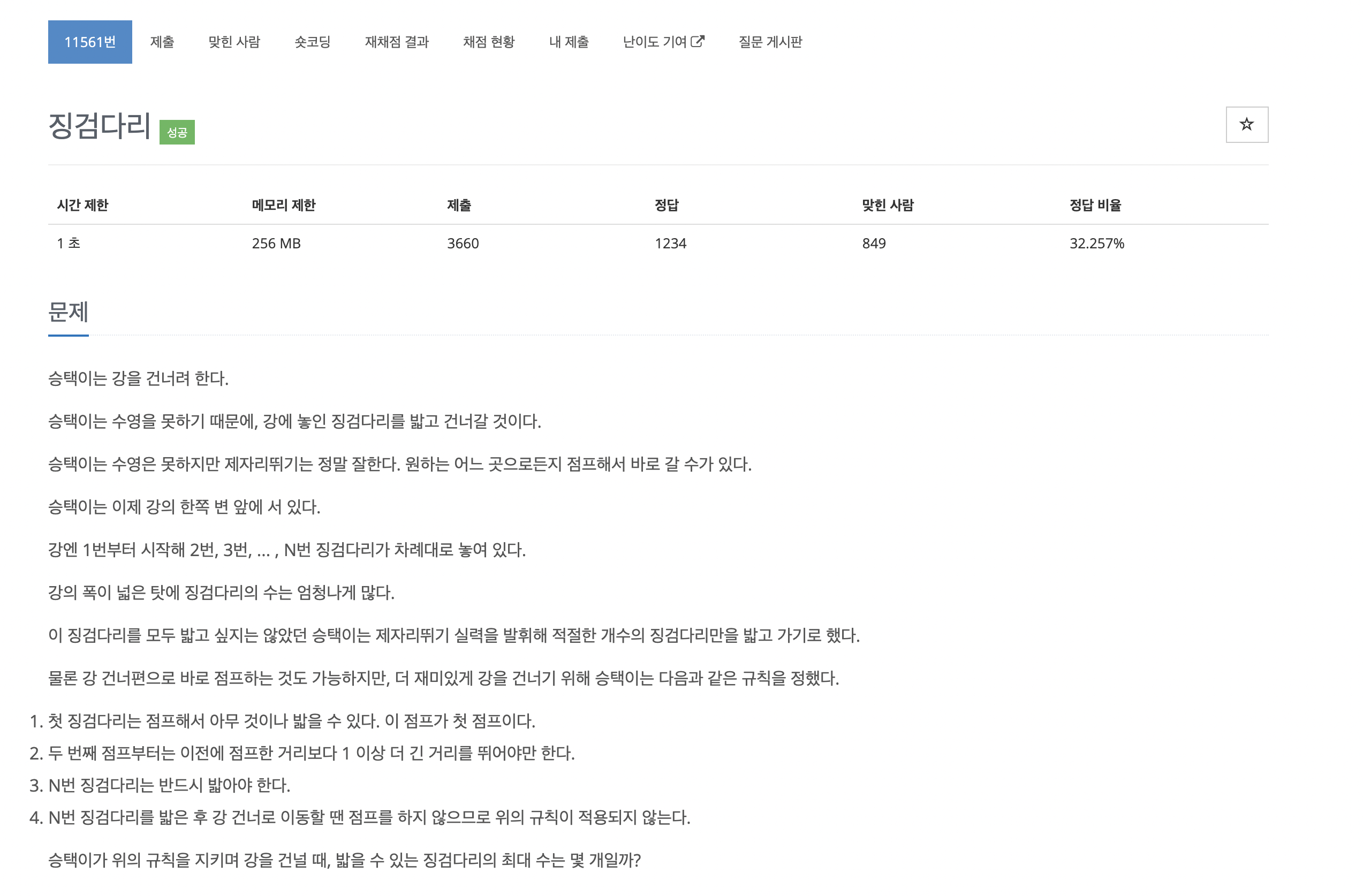
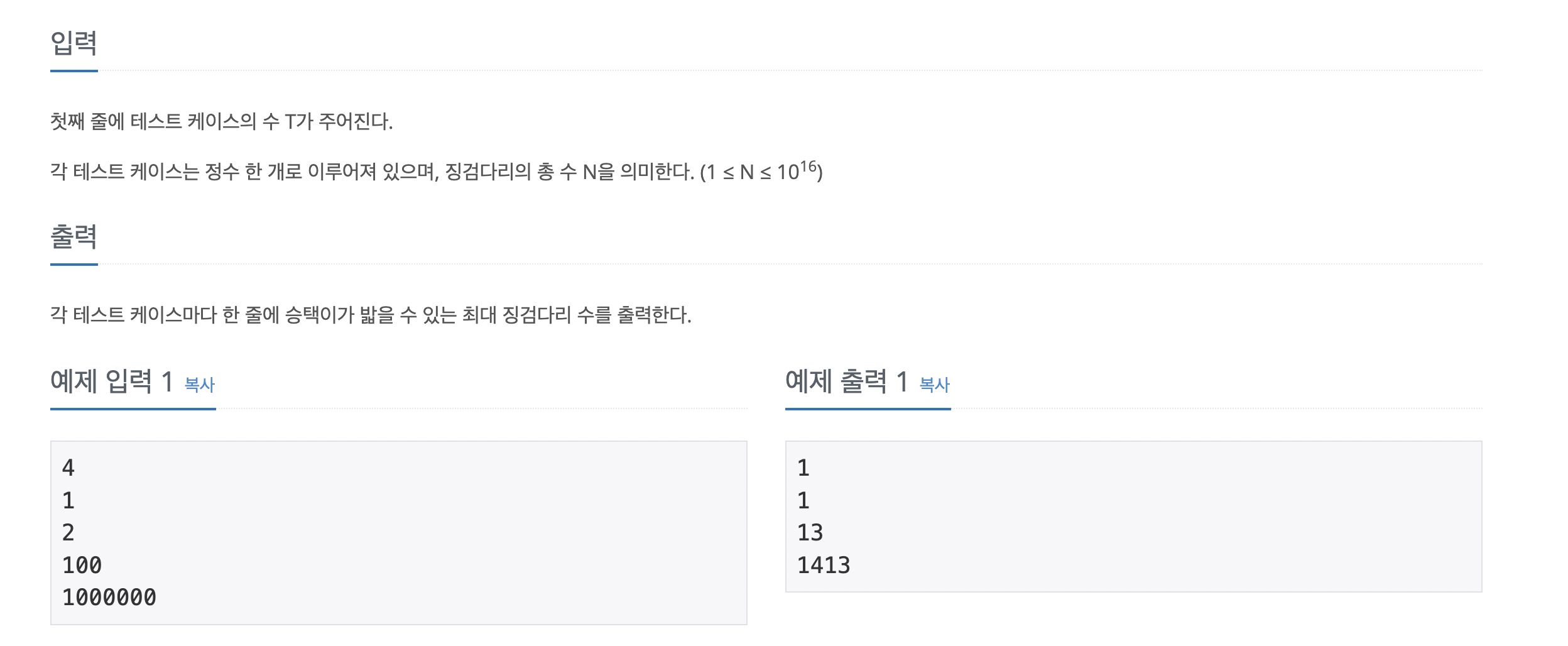
내 이름 오승택!

1. 테스트케이스 T를 입력받고 징검다리의 총 수 n을 T만큼 입력받기

t = int(input())

for _ in range(t):
	n = int(input())

---

2. 이분 탐색 범위 정하기

start = 1
end = n
result = 0 

---

3. 이분 탐색을 통해 밟을 수 있는 최대 징검다리의 총 수 구하기

while start <= end:
		mid = (start + end) // 2
		if ((mid + 1) * mid) // 2 <= n :
			start = mid + 1
			result = mid
		else:
			end = mid - 1

• mid = (start + end) // 2 : 탐색 범위를 계속해서 반으로 줄이면서, 승택이가 밟을 수 있는 징검다리의 최대 수를 찾음.
• if ((mid + 1) * mid) // 2 <= n:
  • 등차수열의 합 공식을 사용. 1부터 mid까지의 합은 (mid * (mid + 1)) // 2로 계산
  • mid 개의 징검다리를 밟기 위해 필요한 최소 거리의 합
  • n보다 작거나 같다면, 이는 mid개의 징검다리를 밟을 수 있다는 뜻.
    -> 더 많은 징검다리를 밟을 수 있는지 확인하기 위해 start를 mid + 1로 설정해 탐색 범위를 오른쪽으로 이동.
    -> 만약 밟을 수 있다면, 더 많은 징검다리를 밟을 수 있는지 확인하기 위해 start를 증가시키고, 현재 mid 값을 result로 저장
  • n보다 크다면, 이는 mid개의 징검다리를 밟을 수 없다는 뜻.
    -> 탐색 범위를 줄여야 한다. 이 경우, end를 mid - 1로 설정하여 왼쪽 부분을 탐색
    

---

전체 풀이

t = int(input())

for _ in range(t):
	n = int(input())
	start = 1
	end = n
	result = 0 
	
	while start <= end:
		mid = (start + end) // 2
		if ((mid + 1) * mid) // 2 <= n :
			start = mid + 1
			result = mid
		else:
			end = mid - 1
	print(result)

---

오늘의 회고

🔥 어제 진행한 이분 탐색을 적용할 수 있는 문제가 나왔지만 등차 수열의 합 공식을 적용하는 생각을 하지 못해 다른 사람의 풀이를 보고 해결할 수 있었다.
🔥 등차 수열에 관한 기본 문제를 진행하고 이분 탐색에 대해 더 공부를 하자!