99클럽 코테 스터디 6일차 이분 탐색/ 이진 탐색

Seongbin·2024년 11월 2일

99클럽 코테 스터디

목록 보기

6/24

오늘의 학습 키워드

이분 탐색/이진 탐색(Binary Search)

이분 탐색(이진 탐색)이란?

정렬되어 있는 리스트에서 탐색 범위를 타노스처럼 절반씩 좁혀가며 데이터를 탐색하는 방법이다.

탐색 기법중 하나로, 탐색하고 싶은 범위를 두 부분으로 분할해서 찾는 방법이다.

두 부분으로 계속 분할해서 조건에 맞는지 찾아가기 때문에, 시간 복잡도가 O(log n)으로 매우 빠른편

무조건 정렬되어 있는 상태에서 이분 탐색을 해야 한다!

오늘의 문제

백준 2805번

https://www.acmicpc.net/problem/2805

입출력

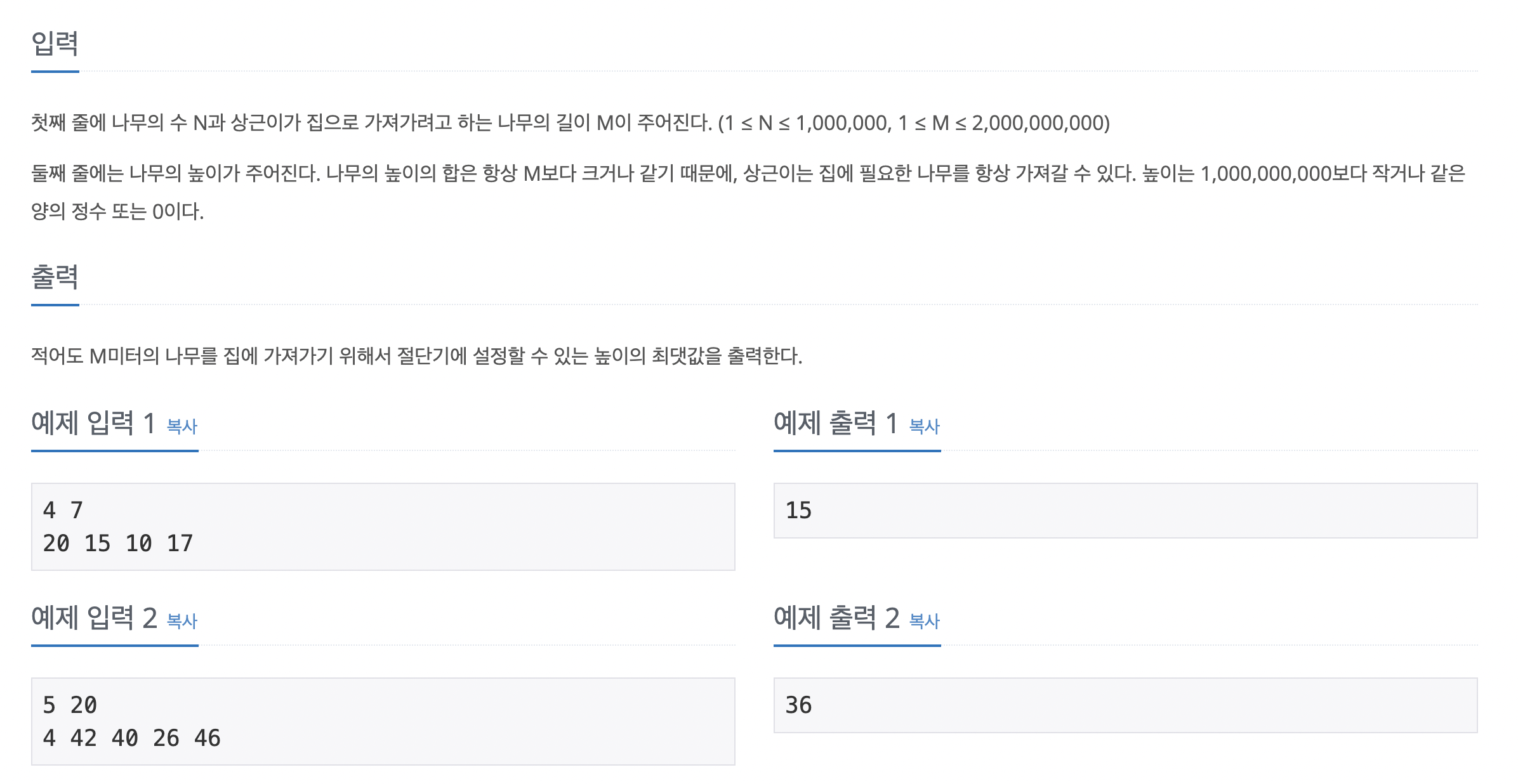
~~상근이 그립다🥲~~

문제 생각해보기

예제 입력에 따르면 20, 15, 10, 17의 길이를 가진 나무들을 높이 15에서 절단하면 5, 0, 0, 2 로 총 7의 길이의 나무를 가져갈 수 있다.

그래서 이걸 왜 이분 탐색으로 푸냐?
탐색 범위를 효율적으로 줄여 나가기 위해서!

절단기의 높이를 설정할 수 있는 값은 0부터 max(trees)까지의 범위인데, 이 범위는 매우 클 수 있다.
예를 들어 나무의 수 N이 최대 1,000,000이고, 나무의 높이가 최대 1,000,000,000이라면, 단순히 모든 높이를 하나씩 탐색하는 방법은 비효율적
이분 탐색은 탐색 범위를 절반씩 줄여 나가는 방식으로, 시간 복잡도가 O(log(max(trees)))

1. 이분 탐색 범위 정하기

n, m = map(int, input().split())
trees = list(map(int, input().split()))

# 이진 탐색을 위한 시작점, 끝점
start = 0
end = max(trees)

start와 end 설정: 절단기의 높이는 최소 0부터 시작하여 최대 나무의 높이(max(trees))까지 설정할 수 있다.

2. 이분 탐색을 통한 최적 높이 찾기

result = 0
while(start <= end):
    total = 0 # 가져갈 나무의 길이
    mid = (start + end) // 2 # 절단기 높이

mid 계산: mid는 현재 탐색 범위의 중간값으로, 절단기의 높이로 설정할 값.
나무 자르기: 각 나무의 높이를 확인하며, mid보다 큰 나무는 잘라서 그 길이를 total에 더하기.

    for i in trees:
        if i > mid: # 절단기보다 주어진 나무가 길면 자른 나머지를 total에 추가
            total += i - mid

예를 들어 mid = 15일 때, 나무가 20인 경우 20 - 15 = 5를 total에 더한다.

3. 탐색 범위 조정:

    if total < m: # 가져가야 하는 길이 m보다 작은 길이이면
        end = mid - 1 # mid 기준 왼쪽 부분 탐색
        
    else: # 가져가야 하는 길이 m보다 크거나 같으면
        result = mid # 절단기 높이를 mid로 설정
        start = mid + 1 # mid 기준 오른쪽 부분 탐색

만약 total이 m보다 작다면, 절단기 높이를 낮춰서 더 많은 나무를 가져가야 하므로 end를 mid - 1로 설정하여 왼쪽 부분을 탐색.
반대로 total이 m 이상이라면, 현재 높이로도 충분히 나무를 가져갈 수 있기 때문에 더 높은 높이에서도 가능한지 확인하기 위해 start를 mid + 1로 설정하여 오른쪽 부분을 탐색. 이때 result를 현재의 mid로 업데이트.

입출력 예시 적용시

입력: n = 4, m = 7, 나무의 높이 [20, 15, 10, 17]
초기 설정: start = 0, end = 20

첫 번째 반복: mid = 10
잘린 나무의 총 길이 = (20 - 10) + (15 - 10) + (17 - 10) = 10 + 5 + 7 = 22 (필요한 길이 7 이상)
result = 10, start = 11

두 번째 반복: mid = 15
잘린 나무의 총 길이 = (20 - 15) + (17 - 15) = 5 + 2 = 7 (필요한 길이 7)
result = 15, start = 16

세 번째 반복: mid = 18

잘린 나무의 총 길이 = (20 - 18) + (17 - 18) = 2 (필요한 길이 7 미만)
end = 17

탐색 종료
반복이 종료되면 result = 15가 최종 답

전체 풀이

n, m = map(int, input().split())
trees = list(map(int, input().split()))

# 이진 탐색을 위한 시작점, 끝점
start = 0
end = max(trees)

result = 0
while(start <= end):
    total = 0 # 가져갈 나무의 길이
    mid = (start + end) // 2 # 절단기 높이
    for i in trees:
        if i > mid: # 절단기보다 주어진 나무가 길면 자른 나머지를 total에 추가
            total += i - mid
            
    # 이분 탐색        
    if total < m: # 가져가야 하는 길이 m보다 작은 길이이면
        end = mid - 1 # mid 기준 왼쪽 부분 탐색
    else: # 가져가야 하는 길이 m보다 크거나 같으면
        result = mid # 절단기 높이를 mid로 설정
        start = mid + 1 # mid 기준 오른쪽 부분 탐색

print(result)

Javascript 풀이

const fs = require('fs');
const input = fs.readFileSync('/dev/stdin').toString().split('\n');

const [n, m] = input[0].split(' ').map(Number);
const trees = input[1].split(' ').map(Number);

// 이진 탐색을 위한 시작점, 끝점
let start = 0;
let end = Math.max(...trees);

let result = 0;
while (start <= end) {
    let total = 0; // 가져갈 나무의 길이
    const mid = Math.floor((start + end) / 2); // 절단기 높이
    
    for (let i = 0; i < trees.length; i++) {
        if (trees[i] > mid) { // 절단기보다 주어진 나무가 길면 자른 나머지를 total에 추가
            total += trees[i] - mid;
        }
    }
    
    // 이분 탐색
    if (total < m) { // 가져가야 하는 길이 m보다 작은 길이이면
        end = mid - 1; // mid 기준 왼쪽 부분 탐색
    } else { // 가져가야 하는 길이 m보다 크거나 같으면
        result = mid; // 절단기 높이를 mid로 설정
        start = mid + 1; // mid 기준 오른쪽 부분 탐색
    }
}

console.log(result);

const fs = require('fs');
const input = fs.readFileSync('/dev/stdin').toString().split('\n');

const fs = require('fs');: Node.js에서 파일 시스템 모듈(fs)을 가져오는 코드. fs는 파일을 읽고 쓰는 작업을 도와줌.
fs.readFileSync('/dev/stdin').toString().split('\n');: 표준 입력(stdin)에서 데이터를 읽음.
readFileSync()는 파일을 동기적으로 읽는 함수.
'/dev/stdin'은 리눅스 시스템에서 표준 입력을 가리키며, 터미널에서 데이터를 읽을 때 사용.
.toString()은 읽은 데이터를 문자열로 변환.
.split('\n')은 읽은 문자열을 줄바꿈(\n)을 기준으로 나누어 배열로 만듦.
예를 들어, 입력이 여러 줄로 이루어져 있다면 각 줄을 개별 요소로 배열에 저장.

const [n, m] = input[0].split(' ').map(Number);
const trees = input[1].split(' ').map(Number);

const [n, m] = input[0].split(' ').map(Number); :
첫 번째 줄의 입력을 가져와서 공백(' ')을 기준으로 나누고, n과 m으로 나눔.
map(Number)는 각 문자열 요소를 숫자로 변환.
const trees = input[1].split(' ').map(Number);: 두 번째 줄의 입력을 가져와서 각 나무의 높이를 배열로 저장.

let start = 0;
let end = Math.max(...trees);

let result = 0;
while (start <= end) {
    let total = 0; // 가져갈 나무의 길이
  	const mid = Math.floor((start + end) / 2); // 절단기 높이

Math.max(...trees); :전달된 숫자들 중에서 가장 큰 값을 반환
...는 스프레드 연산자, 배열의 각 요소를 개별 인수로 확장. 예를 들어, trees가 [20, 15, 10, 17]이라면, Math.max(...trees)는 Math.max(20, 15, 10, 17)와 같은 의미
Math.floor() :내림 연산을 수행, 즉, 주어진 숫자를 가장 가까운 작거나 같은 정수로 반올림.
예를 들어 (start + end) / 2가 5.5라면, Math.floor(5.5)는 5를 반환