99클럽 코테 스터디 8일차 DFS(깊이 우선 탐색)

Seongbin·2024년 11월 4일

99클럽 DFS TIL 개발자취업 깊이 우선 탐색 코딩테스트준비 항해99

99클럽 코테 스터디

목록 보기

8/24

오늘의 학습 키워드

DFS, Depth-First Search(깊이 우선 탐색)

그래프 탐색이란?

하나의 정점으로부터 시작하여 차례대로 모든 정점들을 한 번씩 방문하는 것

Ex) 특정 도시에서 다른 도시로 갈 수 있는지 없는지, 전자 회로에서 특정 단자와 단자가 서로 연결되어 있는지

그러면 DFS란?
루트 노드(혹은 다른 임의의 노드)에서 시작해서 다음 분기(branch)로 넘어가기 전에 해당 분기를 완벽하게 탐색하는 방법

미로를 탐색할 때 한 방향으로 갈 수 있을 때까지 계속 가다가 더 이상 갈 수 없게 되면 다시 가장 가까운 갈림길로 돌아와서 이곳으로부터 다른 방향으로 다시 탐색을 진행하는 방법과 유사하다.
즉, 넓게(wide) 탐색하기 전에 깊게(deep) 탐색하는 것이다.
사용하는 경우: 모든 노드를 방문 하고자 하는 경우에 이 방법을 선택한다.
깊이 우선 탐색(DFS)이 너비 우선 탐색(BFS)보다 좀 더 간단하다.
단순 검색 속도 자체는 너비 우선 탐색(BFS)에 비해서 느리다.

깊이 우선 탐색(DFS)의 특징

자기 자신을 호출하는 순환 알고리즘의 형태 를 가지고 있다.
이 알고리즘을 구현할 때 가장 큰 차이점은, 그래프 탐색의 경우 어떤 노드를 방문했었는지 여부를 반드시 검사 해야 한다는 것이다.이를 검사하지 않으면 무한 루프에 빠질 수도 있다.
찾고자하는 답이 트리에서부터 멀어질 수록 DFS가 유리하다. (BFS에 비해)

오늘의 문제

백준 2644번

https://www.acmicpc.net/problem/2644

문제 설명

입출력 예

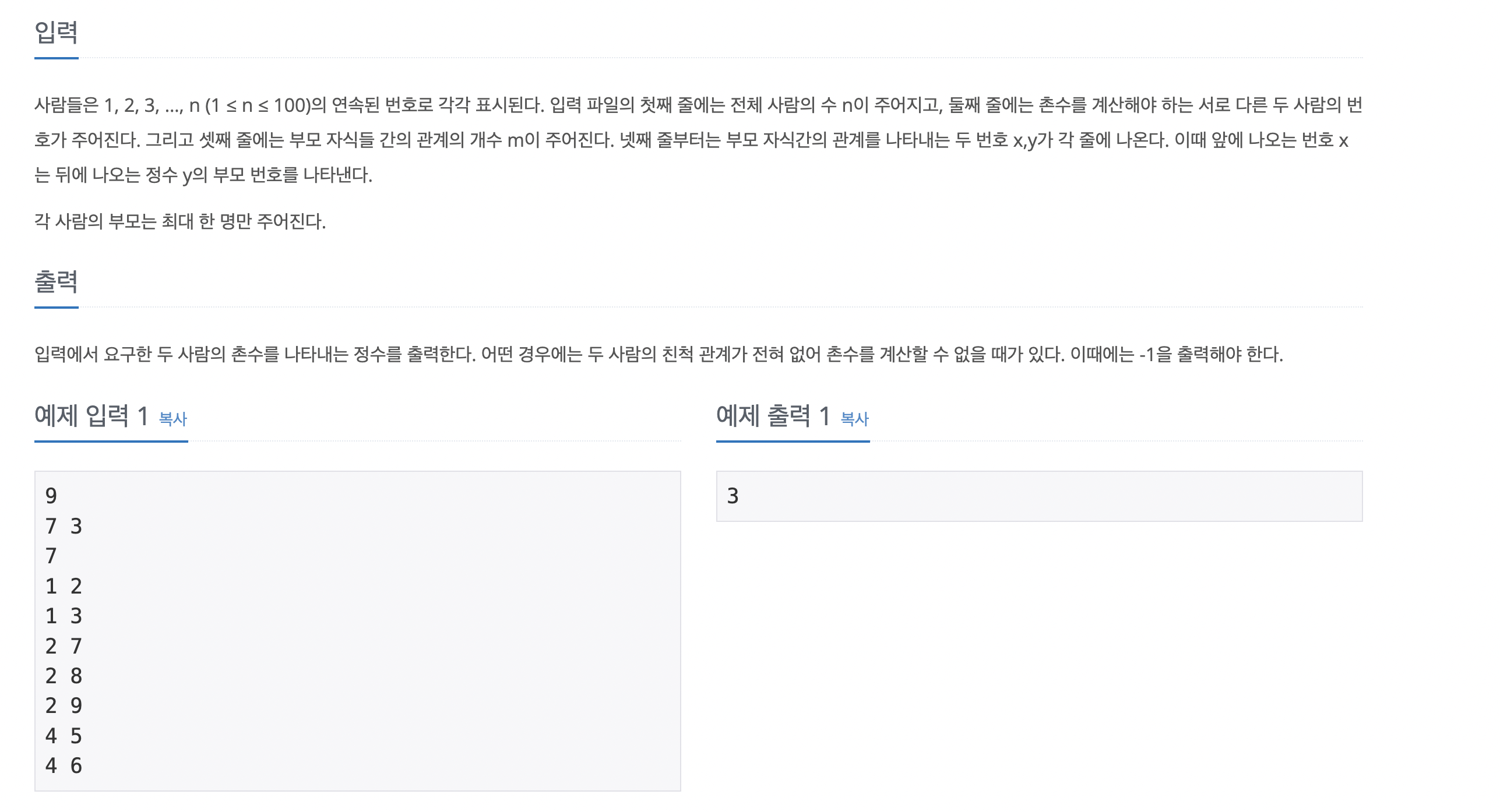
문제 생각해보기

위 입출력 예시1에 따르면 그래프의 그림은 이렇게 된다.

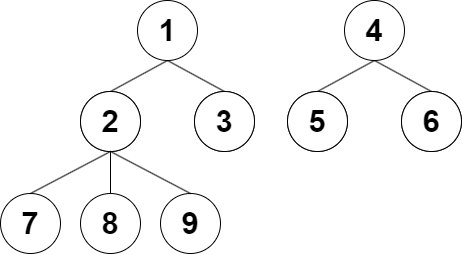
DFS 탐색 순서

오름차순 방문: DFS 탐색 시 인접 정점들을 오름차순으로 방문.

시작 노드는 start이다. 시작 노드에서부터 탐색을 시작하며, 첫 번째로 start를 방문했음을 기록하고 깊이를 증가시킨다.
현재 노드가 목표 노드 end와 일치하는지 확인한다. 만약 일치한다면, 탐색은 종료되고 relation_depth 리스트에 해당 깊이를 기록한다.
방문하지 않은 인접 노드를 모두 확인하고, 오름차순으로 탐색을 진행한다. 각 인접 노드에 대해 재귀적으로 DFS를 호출하여 촌수를 계속 계산한다.
인접 노드를 모두 방문하거나 목표 노드를 찾을 때까지 탐색을 계속한다. 목표 노드를 찾으면 결과를 relation_depth 리스트에 저장한다.
만약 목표 노드에 도달하지 못하면, 이는 두 노드 사이에 친척 관계가 없다는 의미이므로 -1을 출력한다.

1. 입력 처리

n = int(input())  # 전체 사람의 수
start, end = map(int, input().split())  # 촌수를 계산해야 하는 두 사람의 번호
m = int(input())  # 부모 자식 관계의 개수

n = int(input()) : 전체 사람의 수를 입력받는다.
start, end = map(int, input().split()): 촌수를 계산하고자 하는 두 사람의 번호를 입력받는다.
m = int(input()) : 부모 자식 관계의 개수를 입력받는다.
이 단계에서는 전체 사람 수, 촌수를 계산할 두 사람, 그리고 관계의 개수를 입력받아 문제를 해결하기 위한 기본 정보를 수집한다.

2. 그래프와 방문 기록 초기화

# 그래프와 방문 기록 초기화
graph = [[] for _ in range(n + 1)]  # 각 사람의 관계를 나타내는 인접 리스트
visited = [False] * (n + 1)  # 방문 여부를 기록하는 리스트
relation_depth = []  # 결과 촌수 저장 리스트

graph = [[] for _ in range(n + 1)] : 각 사람 간의 관계를 나타내는 인접 리스트를 초기화한다. 사람들의 번호가 1부터 시작하므로 인덱스 0은 사용하지 않기 위해 n + 1 크기로 생성한다.
visited = [False] * (n + 1) : 각 사람이 방문되었는지 여부를 기록하는 리스트이다. 초기에는 모두 False로 설정되어 방문되지 않았음을 의미한다.
relation_depth = []: 두 사람 간의 촌수를 저장하기 위한 리스트이다. 목표 노드에 도달했을 때만 값을 추가한다.
이 단계에서는 그래프 구조와 각 노드의 방문 여부를 추적하기 위한 초기화를 진행한다.

3. 부모 자식 관계 입력 및 그래프 구성

# 부모 자식 관계 입력 및 그래프 구성
for _ in range(m):
    x, y = map(int, input().split())
    graph[x].append(y)
    graph[y].append(x)

for _ in range(m): : 부모 자식 관계의 개수만큼 반복하여 관계를 입력받는다.
x, y = map(int, input().split()) : 각 부모 자식 관계를 입력받아 x와 y로 저장한다.
graph[x].append(y)와 graph[y].append(x) : 입력된 관계를 양방향으로 저장하여 두 사람 간의 연결을 표현한다. 이렇게 함으로써 무방향 그래프 형태로 관계를 나타낸다.
이 단계에서는 그래프에 부모 자식 관계를 저장하여, 각 노드 간의 연결 정보를 구성한다.

4. 깊이 우선 탐색(DFS) 함수 정의

# 깊이 우선 탐색 (DFS) 정의
def dfs(current, depth):
    depth += 1
    visited[current] = True

    if current == end:
        relation_depth.append(depth)
        return

    for neighbor in graph[current]:
        if not visited[neighbor]:
            dfs(neighbor, depth)

def dfs(current, depth) : 현재 방문 중인 노드와 현재까지의 깊이를 인자로 받는 DFS 함수이다.
depth += 1 : 현재 노드의 깊이를 1 증가시킨다. 이는 촌수를 의미한다.
visited[current] = True : 현재 노드를 방문 처리하여 다시 방문하지 않도록 한다.
if current == end : 만약 현재 노드가 목표 노드와 일치한다면, relation_depth에 현재 깊이를 저장하고 탐색을 종료한다. 즉, 목표 노드에 도달했음을 의미한다.
for neighbor in graph[current] : 현재 노드와 연결된 모든 이웃 노드를 순회한다.
if not visited[neighbor] : 방문하지 않은 이웃 노드에 대해 재귀적으로 DFS를 호출하여 촌수를 계산한다.
이 단계에서는 DFS를 사용하여 모든 경로를 탐색하고 목표 노드에 도달하는 경우 그 깊이를 기록한다.

5. DFS 실행 및 결과 출력

# DFS 실행 및 결과 출력
dfs(start, 0)

# 촌수 계산 결과 출력
if len(relation_depth) == 0:
    print(-1)  # 친척 관계가 없는 경우
else:
    print(relation_depth[0] - 1)  # 촌수 출력 (depth에서 1을 뺌)

dfs(start, 0) : 시작 노드와 깊이 0으로 DFS 탐색을 시작한다. 시작 노드에서부터 목표 노드까지의 촌수를 계산한다.
if len(relation_depth) == 0 : 만약 목표 노드에 도달하지 못한 경우, 두 사람 간의 친척 관계가 없음을 의미하므로 -1을 출력한다.
else: print(relation_depth[0] - 1) : 목표 노드에 도달한 경우, 저장된 깊이에서 1을 빼서 최종 촌수를 출력한다. 깊이는 탐색 중 증가하기 때문에, 실제 촌수는 depth - 1이 된다.
이 단계에서는 DFS를 실행하고 결과를 출력하여 최종적으로 두 사람 간의 촌수를 계산한다.

전체 풀이

n = int(input())  # 전체 사람의 수
start, end = map(int, input().split())  # 촌수를 계산해야 하는 두 사람의 번호
m = int(input())  # 부모 자식 관계의 개수

# 그래프와 방문 기록 초기화
graph = [[] for _ in range(n + 1)]  # 각 사람의 관계를 나타내는 인접 리스트
visited = [False] * (n + 1)  # 방문 여부를 기록하는 리스트
relation_depth = []  # 결과 촌수 저장 리스트

# 부모 자식 관계 입력 및 그래프 구성
for _ in range(m):
    x, y = map(int, input().split())
    graph[x].append(y)
    graph[y].append(x)

# 깊이 우선 탐색 (DFS) 정의
def dfs(current, depth):
    depth += 1
    visited[current] = True

    if current == end:
        relation_depth.append(depth)
        return

    for neighbor in graph[current]:
        if not visited[neighbor]:
            dfs(neighbor, depth)

# DFS 실행 및 결과 출력
dfs(start, 0)

# 촌수 계산 결과 출력
if len(relation_depth) == 0:
    print(-1)  # 친척 관계가 없는 경우
else:
    print(relation_depth[0] - 1)  # 촌수 출력 (depth에서 1을 뺌)