
다익스트라(Dijkstra)
지난 시간에 우선순위 큐를 단독으로 구현하는 문제는 없고, 이를 이용하여 코테에 종종 나오는 다익스트라 문제에 쓸 수 있다고 하였다.
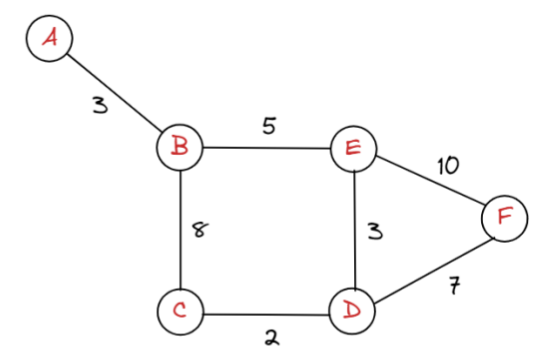
위의 그림에서 만약에 간선에 가중치가 없다고 하면, A에서 D까지 가는 최단 경로는
A->B->E->D 또는 A->B->C->D 2가지 경로가 존재할 것이다.
그러나, 다익스트라 알고리즘은 간선에 비용(가중치)가 있기 때문에 위 그림의 최적의 경로는 3+5+3=11 비용이 드는 A->B->E->D이다.
👉이와 같이, 다익스트라 알고리즘은 가중치 그래프에서 시작점과 도착점이 주어졌을 때, 최소 비용을 return하는 알고리즘을 말한다.
- 가중치가 없으면(또는 모든 가중치가 1), BFS 알고리즘을 사용하면 된다.
📜다익스트라 알고리즘 진행 과정과정
📢다익스트라 알고리즘은 BFS + Priority queue를 합친 알고리즘이라고 보면 된다. 즉, 큐를 이용해서 인접 노드를 순회하면서 탐색하는 과정은 BFS와 비슷한데, 간선에 가중치가 있다보니 Priority queue를 사용해서(가중치가 우선순위인 min heap) 최단 경로를 찾는 알고리즘이라 할 수 있다.
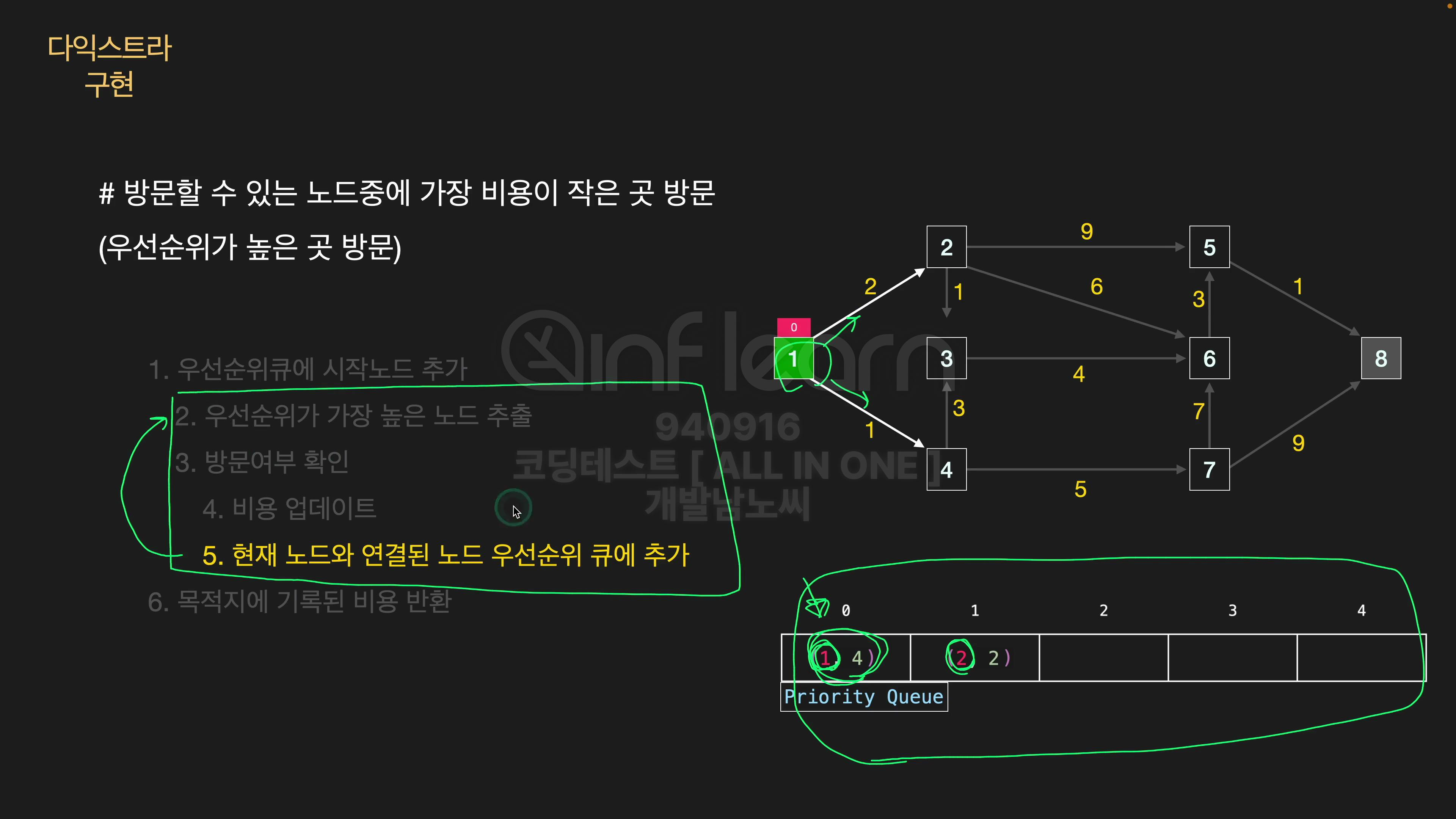
우선순위 큐가 비어있을 때까지 2번 과정을 계속해서 반복한다.(BFS와 비슷한듯...?)
- 비용 업데이트 단계에서, 해당하는 노드까지의 비용과 노드번호를 우선순위 큐에 삽입한다.
⚙코드 설계
위의 알고리즘 진행 과정을 하나씩 코드로 구현해보자. (단, graph와 시작점 및 도착점은 주어졌다고 가정한다.)
1. 우선순위 큐에 시작노드 추가
def dijkstra(graph, start, final):
costs = {} # 비용 업데이트를 위한 딕셔너리
pq = [] # 우선순위 큐는 리스트로 구현
heapq.heappush(pq, (0, start)) # 시작점의 비용은 0이므로, 우선순위 큐에 추가 - 📢튜플 앞 원소를 기준으로 비교하기 때문에
heappush()를 할 때는 비용을 앞에 놓는다. - 이 과정은 BFS의 사전 세팅을 하는 것과 비슷한데, BFS에서는
visited = [start_v]와q = deque(start_v)를 했다.
즉, visited가 costs로, q가 priority queue로 대체됬다고 보면 된다.
2. 우선순위가 가장 높은 노드 추출
📢여기에서 BFS와 비슷한 알고리즘이 나온다.(결국 큐는 인접 노드를 탐색하는 자료구조)
while q:
cur_cost, cur_v = heappop(pq)
# if cur_v == final: # 현재노드가 도착점이면
# return cur_cost # 도착점까지의 비용을 리턴- 💡원래 코드에는
if cur_v == final:가 없었는데, 불필요한 탐색(모든 노드를 라벨링)을 실행하지 않기 위해 추가하였다.
->(수정) Network Delay time 문제를 풀면, 모든 노드를 라벨링해야 하기 때문에 이 코드는 필요가 없음 (심지어 최적화를 하지 않아도 Worst Case는O(ElogV)이기 때문에 괜춘)
3. 방문여부 확인(4. 비용 업데이트, 5. 현재 노드와 연결된 노드 우선순위 큐에 추가)
if cur_v not in costs: # 현재 노드가 costs에 방문하지 않았으면
costs[cur_v] = cur_cost # key: cur_v, value: cur_cost로 저장
for next_v, cost in graph[cur_v]: # 인접 노드(딕셔너리의 value)들을 순회하면서 탐색
next_cost = cur_cost + cost # 비용 업데이트(현재노드까지의 비용 + 간선 비용)
heapq.heappush((pq, (next_cost, next_v)) 🤔왜 강의 코드는 for cost, next_v in graph[cur_v]: 인데 for next_v, cost in graph[cur_v]:로 고쳤나요?
우리가 자료구조를 공부해보면 G=(V,E)와 같이 그래프를 수식으로 표현하는데, 이것에 맞춰서 표현하기 위해서다.
6. (우선순위 큐가 비어있으면) 목적지에 기록된 비용 반환
return costs[final] # 최소 비용을 리턴💻코드 구현
def dijkstra(graph, start, final):
costs = {} # 방문 여부
pq = [] # 우선순위 큐
heapq.heappush(pq, (0, start)) # 시작 노드 추가
while pq:
cur_cost, cur_v = heapq.heappop(pq)
# if cur_v == final:
# return cur_cost
if cur_v not in costs: # 방문여부 확인
costs[cur_v] = cur_cost
# 인접 노드 탐색하면서 비용 업데이트
for next_v, cost in graph[cur_v]: # 현재노드와 연결된 인접노드와 그 비용
next_cost = cur_cost + cost
heapq.heappush(pq, (next_cost, next_v))
return costs[final]📢명심하자! 우선순위 큐는 비용을 기준으로 하니까 (E,V)와 같이 Edge의 비용을 튜플 앞에 두고, 방문했는지 확인하기 위한 costs 딕셔너리는 G=(V,E)의 수식을 따라서 costs[cur_v] = cur_cost로 저장할 것!!
