지난 시간에는 대부분의 비선형구조인 트리, 그래프, 힙에 많이 사용되는 재귀를 학습했는데 이번 시간에는 비선형구조 중 하나인 트리를 배워보겠습니다.
🔎먼저 트리의 정의와 용어를 알아보겠습니다.
🔖트리: 서로 연결된 Node의 계층형 자료구조로서, root와 부모-자식 관계의 subtree로 구성되어 있는 구조를 말한다.
💡선형 자료구조란 하나의 자료 뒤에 하나의 자료가 존재하는 것을 말하며, 비선형 자료구조는 하나의 자료 뒤에 여러 개의 자료가 존재하는 것을 말합니다.
- 링크드 리스트는 물리적으로는 연속해서 연결되어 있지 않지만, 포인터를 사용해서 논리적으로 연속성이 있기 때문에 선형구조로 분류됩니다.
트리 관련 용어
- 정점(Vertex): 노드로 표현되며, value를 갖는다.
- 간선(Edge): 정점 간에 연결된 선
- 부모(Parent)-자식(Child) 노드: root로 보면 아래 계층의 노드들이 Child 노드가 되고, Child 노드가 subtree에서 부모 역할을 하면 부모 노드가 되고 Child의 subChild는 자식 노드가 된다.
👉그래서 재귀 함수를 활용하면 전체적인 트리 구조에 subtree가 여러 개 있다는 의미가 된다. - 리프(Leaf) 노드: 자식 노드가 없는 마지막 노드를 말한다.
- 차수(degree): 각 노드가 갖는 자식 노드의 수를 말함
- 모든 노드의 차수가 n개 이하이면 n진 트리라고 한다.
- 조상(Ancestor): 위쪽으로 간선을 따라가면 만나는 모든 노드
- 자손(Descendant): 아래쪽으로 간선을 따라가면 만나는 모든 노드
- 높이(Height): root 노드에서 가장 멀리 떨어진 리프 노드까지의 거리
- 레벨(Level): root 노드에서 떨어진 거리
트리를 만드는 방법은 간단하다. Node 클래스를 이용해서 left와 right에 새 노드를 가리키게만 해주면 된다.
public class Main {
public static void main(String[] args) {
Node root = new Node(1);
root.left = new Node(2);
root.right = new Node(3);
root.left.left = new Node(4);
root.left.right = new Node(5);
root.right.right = new Node(6);
}
public static class Node {
int value;
Node left;
Node right;
public Node(int value) {
this.value = value;
this.left = null;
this.right = null;
}
}
}트리 순회
선형 자료구조인 배열과 링크드 리스트의 경우, for문 안에서 인덱스를 기반으로 탐색을 쉽게 할 수 있기 때문에 순회 방법을 따로 배우지 않았습니다.
그러나, 트리는 비선형 자료구조이기 때문에 level order traversal, preorder traversal, inorder traversal, 그리고 postorder traversal과 같이 여러가지 방법이 있습니다.
이번 시간에는 그래프의 bfs(breadth-first-search)와 비슷한 level order traversal을 배워보겠습니다.
level order traversal
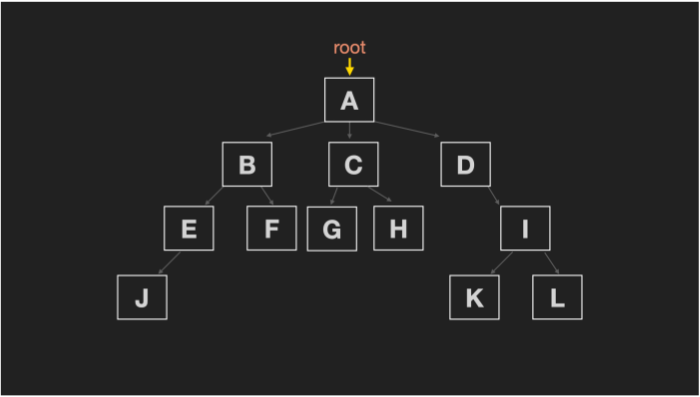
위와 같이 root로부터 시작되는 트리가 있다고 가정하겠습니다. 앞선 용어 정리에서 level은 "root 노드로부터 떨어진 거리"라고 했는데요, level order traversal은 level 별로 노드를 방문하는 방법을 말하기 때문에 노드 방문 순서는 다음과 같습니다:
level 0: A
level 1: B -> C -> D
level 2: E -> F -> G -> H -> I
level 3: J -> K -> L
⚙️코드 설계
강사님께서는 levelorder 코드 템플릿을 그냥 손이 자동으로 칠 정도로 암기하라고 하셨지만, 저는 맹목적인 암기는 지양하는 편이기 때문에 순서대로 알고리즘을 작성해보겠습니다.
📢노드의 방문과 접근을 다르게 보기 위해 방문은 visited라는 배열을, 노드에 접근해서 인접 노드가 있는지 확인하기 위한 자료구조는 FIFO(First-In-First-Out)의 Deque를 사용합니다.
- (base condition): 만약 root가 null이면 0을 리턴
- visited 리스트를 생성하고, 처음에 root 노드에 하위 레벨의 노드가 있는지 탐색하기 위해 덱에 삽입
- 덱에 현재 노드를 삭제 후, 방문에 추가
3.1. 만약 현재 노드의 왼쪽에 노드가 있으면 덱에 추가
3.2. 만약 현재 노드의 오른쪽에 노드가 있으면 덱에 추가 - 덱이 비었으면 방문 배열을 리턴
💻코드 구현
package src.recursion.tree;
import java.util.*;
class Node {
int value;
Node left;
Node right;
public Node(int value) {
this.value = value;
this.left = null;
this.right = null;
}
}
public class LevelOrderTraversal {
public List<Integer> levelOrder(Node root) {
// base condition
if (root == null) {
return new ArrayList<>(); // null 대신 빈 리스트를 반환해야 안전
}
// 사전 세팅
List<Integer> visited = new ArrayList<>();
Queue<Node> q = new LinkedList<>();
// Enqueue Root
q.offer(root);
// 인접 노드 탐색
while (!q.isEmpty()) {
// Dequeue a front node in the queue
Node curNode = q.poll();
visited.add(curNode.value);
if (curNode.left != null) {
q.offer(curNode.left);
}
if (curNode.right != null) {
q.offer(curNode.right);
}
}
return visited;
}
}- base condition에서 null을 리턴하면 NullPointerException이 터질 수 있으므로 빈 ArrayList를 반환하였다.
💡파이썬에서는 collections 라이브러리를 사용해서 deque 자료구조를 사용했지만, 자바에서는 런타임 실행 중에 예외가 터지면 프로그램이 종료되기 때문에 다음과 같은 이유로 add -> offer, remove -> poll 메서드를 사용한다. add()는 큐에 요소를 추가할 때, 큐가 꽉 차면 IllegalStateException 예외를 발생offer()는 큐가 꽉 차면 false를 반환
remove()는 큐가 비어 있을 때 NoSuchElementException 예외를 발생poll()은 큐가 비어 있으면 null을 반환
🔖polling: 네트워크나 컴퓨터 과학에서는 상태를 주기적으로 감시하거나 확인하는 행위를 의미하는데, 큐에서는 큐의 상태(맨 앞 요소)를 확인하고 꺼내는 동작을 말한다.
