데이터 저장-자료구조-종류

Array vs Linked List

Array

특징

• 논리적 저장 순서와 물리적 저장 순서가 일치.

• 따라서 인덱스(index)로 해당 원소(element)에 접근 가능. 그렇기 때문에 찾고자 하는 원소의 인덱스 값을 알고 있으면 Big-O(1)에 해당 원소로 접근.

• random access 가 가능.

• 문제는 삭제 또는 삽입의 과정에서는 해당 원소에 접근하여 작업을 완료한 뒤(O(1)), 또 한 가지의 작업을 추가적으로 해줘야 하기 때문에, 시간이 더 걸림.

• 만약 배열의 원소 중 어느 원소를 삭제했다고 했을 때, 배열의 연속적인 특징이 깨지게 된서 빈 공간이 생김. 따라서 삭제한 원소보다 큰 인덱스를 갖는 원소들을 shift해줘야 하는 비용(cost)이 발생하고 이 경우의 시간 복잡도는 O(n)됨. 그렇기 때문에 Array 자료구조에서 삭제 기능에 대한 time complexity 의 worst case 는 O(n).

• 삽입의 경우도 만약 첫번째 자리에 새로운 원소를 추가하고자 한다면 모든 원소들의 인덱스를 1 씩 shift 해줘야 하므로 이 경우도 O(n).

Linked List

특징

• ArrayList의 문제점을 해결하기 위한 자료구조. 각각의 원소들은 자기 자신 다음에 어떤 원소인지만을 기억.

• 따라서 이 부분만 다른 값으로 바꿔주면 삭제와 삽입을 O(1) 만에 해결할 수 있음.

• 문제는 원하는 위치에 삽입을 하고자 하면 원하는 위치를 Search 과정에 있어서 첫번째 원소부터 다 확인해야함.

• Array 와는 달리 논리적 저장 순서와 물리적 저장 순서가 일치하지 않다. 삽입하고 정렬하는 것과 마찬가지. 이 과정 때문에, 어떠한 원소를 삭제 또는 추가하고자 했을 때, 그 원소를 찾기 위해서 O(n)의 시간이 추가적으로 발생.

• 결국 linked list는 search 에도 O(n)의 time complexity 를 갖고, 삽입, 삭제에 대해서도 O(n)의 time complexity. 그렇다고 해서 아주 쓸모없는 자료구조는 아니고 Tree 구조의 근간이 되는 자료구조이며, Tree 에서 사용되었을 때 유용함.

구현 추천

Array 를 기반으로한 Linked List 구현
ArrayList 를 기반으로한 Linked List 구현

구현 예제 JS

var LinkedList = function () {
  var list = {};
  list.head = null;
  list.tail = null;

  list.addToTail = function (value) {
    let node = new Node(value);

    if (!this.head) {
      this.head = node;
      this.tail = node;
    } else {
      this.tail.next = node;
      this.tail = node;
    }
  };

  list.removeHead = function () {
    let removeNode = this.head;
    if (TimeRanges.head !== null) {
      this.head = removeNode.next;
      return removeNode.value;
    }
  };

  list.contains = function (target) {
    let accNode = this.head;
    while (accNode) {
      if (accNode.value === target) {
        return true;
      }
      accNode = accNode.next;
    }
    return false;
  };

  return list;
};



var Node = function (value) {
  var node = {};

  node.value = value;
  node.next = null;

  return node;
};

Stack and Queue

Stack

특징

• 선형 자료구조의 일종으로 Last In First Out (LIFO). 즉, 나중에 들어간 원소가 먼저 나옴.

Queue

특징

• 선형 자료구조의 일종으로 First In First Out (FIFO). 즉, 먼저 들어간 놈이 먼저 나옴.
• Java Collection 에서 Queue 는 인터페이스. 이를 구현하고 있는 Priority queue등을 사용할 수 있음.

Personal Recommendation
Stack 을 사용하여 미로찾기 구현하기
Queue 를 사용하여 Heap 자료구조 구현하기
Stack 두 개로 Queue 자료구조 구현하기
Stack 으로 괄호 유효성 체크 코드 구현하기
뒤로/위로

Tree

특징

• 트리는 스택이나 큐와 같은 선형 구조가 아닌 비선형 자료구조.
• 트리는 계층적 관계(Hierarchical Relationship)을 표현. 이 트리라는 자료구조는 표현에 집중. 무엇인가를 저장하고 꺼내야 한다는 사고에서 벗어나 트리라는 자료구조를 바라보자.

트리를 구성하고 있는 구성요소들(용어)
Node (노드) : 트리를 구성하고 있는 각각의 요소를 의미한다.
Edge (간선) : 트리를 구성하기 위해 노드와 노드를 연결하는 선을 의미한다.
Root Node (루트 노드) : 트리 구조에서 최상위에 있는 노드를 의미한다.
Terminal Node ( = leaf Node, 단말 노드) : 하위에 다른 노드가 연결되어 있지 않은 노드를 의미한다.
Internal Node (내부노드, 비단말 노드) : 단말 노드를 제외한 모든 노드로 루트 노드를 포함한다.

Binary Tree (이진 트리)

루트 노드를 중심으로 두 개의 서브 트리(큰 트리에 속하는 작은 트리)로 나뉘어 진다. 또한 나뉘어진 두 서브 트리도 모두 이진 트리어야 한다. 재귀적인 정의라 맞는듯 하면서도 이해가 쉽지 않을 듯하다. 한 가지 덧붙이자면 공집합도 이진 트리로 포함시켜야 한다. 그래야 재귀적으로 조건을 확인해갔을 때, leaf node 에 다다랐을 때, 정의가 만족되기 때문이다. 자연스럽게 노드가 하나 뿐인 것도 이진 트리 정의에 만족하게 된다.

트리에서는 각 층별로 숫자를 매겨서 이를 트리의 Level(레벨)이라고 한다. 레벨의 값은 0 부터 시작하고 따라서 루트 노드의 레벨은 0 이다. 그리고 트리의 최고 레벨을 가리켜 해당 트리의 height(높이)라고 한다.

Perfect Binary Tree (포화 이진 트리), Complete Binary Tree (완전 이진 트리), Full Binary Tree (정 이진 트리)
모든 레벨이 꽉 찬 이진 트리를 가리켜 포화 이진 트리라고 한다. 위에서 아래로, 왼쪽에서 오른쪽으로 순서대로 차곡차곡 채워진 이진 트리를 가리켜 완전 이진 트리라고 한다. 모든 노드가 0개 혹은 2개의 자식 노드만을 갖는 이진 트리를 가리켜 정 이진 트리라고 한다. 배열로 구성된 Binary Tree는 노드의 개수가 n 개이고 root가 0이 아닌 1에서 시작할 때, i 번째 노드에 대해서 parent(i) = i/2 , left_child(i) = 2i , right_child(i) = 2i + 1 의 index 값을 갖는다.

BST (Binary Search Tree)

효율적인 탐색을 위해서는 어떻게 찾을까만 고민해서는 안된다. 그보다는 효율적인 탐색을 위한 저장방법이 무엇일까를 고민해야 한다. 이진 탐색 트리는 이진 트리의 일종이다. 단 이진 탐색 트리에는 데이터를 저장하는 규칙이 있다. 그리고 그 규칙은 특정 데이터의 위치를 찾는데 사용할 수 있다.

규칙 1. 이진 탐색 트리의 노드에 저장된 키는 유일하다.
규칙 2. 부모의 키가 왼쪽 자식 노드의 키보다 크다.
규칙 3. 부모의 키가 오른쪽 자식 노드의 키보다 작다.
규칙 4. 왼쪽과 오른쪽 서브트리도 이진 탐색 트리이다.
이진 탐색 트리의 탐색 연산은 O(log n)의 시간 복잡도를 갖는다. 사실 정확히 말하면 O(h)라고 표현하는 것이 맞다. 트리의 높이를 하나씩 더해갈수록 추가할 수 있는 노드의 수가 두 배씩 증가하기 때문이다. 하지만 이러한 이진 탐색 트리는 Skewed Tree(편향 트리)가 될 수 있다. 저장 순서에 따라 계속 한 쪽으로만 노드가 추가되는 경우가 발생하기 때문이다. 이럴 경우 성능에 영향을 미치게 되며, 탐색의 Worst Case 가 되고 시간 복잡도는 O(n)이 된다.

배열보다 많은 메모리를 사용하며 데이터를 저장했지만 탐색에 필요한 시간 복잡도가 같게 되는 비효율적인 상황이 발생한다. 이를 해결하기 위해 Rebalancing 기법이 등장하였다. 균형을 잡기 위한 트리 구조의 재조정을 Rebalancing이라 한다. 이 기법을 구현한 트리에는 여러 종류가 존재하는데 그 중에서 하나가 뒤에서 살펴볼 Red-Black Tree이다.

Personal Recommendation
Binary Search Tree 구현하기
주어진 트리가 Binary 트리인지 확인하는 알고리즘 구현하기

Tree-Heap

Binary Heap

자료구조의 일종으로 Tree 의 형식을 하고 있으며, Tree 중에서도 배열에 기반한 Complete Binary Tree이다. 배열에 트리의 값들을 넣어줄 때, 0 번째는 건너뛰고 1 번 index 부터 루트노드가 시작된다. 이는 노드의 고유번호 값과 배열의 index 를 일치시켜 혼동을 줄이기 위함이다. 힙(Heap)에는 최대힙(max heap), 최소힙(min heap) 두 종류가 있다.

Max Heap

각 노드의 값이 해당 children 의 값보다 크거나 같은 complete binary tree를 말한다. ( Min Heap 은 그 반대이다.)

Max Heap에서는 Root node 에 있는 값이 제일 크므로, 최대값을 찾는데 소요되는 연산의 time complexity 이 O(1)이다. 그리고 complete binary tree이기 때문에 배열을 사용하여 효율적으로 관리할 수 있다. (즉, random access 가 가능하다. Min heap 에서는 최소값을 찾는데 소요되는 연산의 time complexity 가 O(1)이다.) 하지만 heap 의 구조를 계속 유지하기 위해서는 제거된 루트 노드를 대체할 다른 노드가 필요하다. 여기서 heap 은 맨 마지막 노드를 루트 노드로 대체시킨 후, 다시 heapify 과정을 거쳐 heap 구조를 유지한다. 이런 경우에는 결국 O(log n)의 시간복잡도로 최대값 또는 최소값에 접근할 수 있게 된다.

Personal Recommendation
Heapify 구현하기

Red Black Tree

RBT(Red-Black Tree)는 BST 를 기반으로하는 트리 형식의 자료구조이다. 결론부터 말하자면 Red-Black Tree 에 데이터를 저장하게되면 Search, Insert, Delete 에 O(log n)의 시간 복잡도가 소요된다. 동일한 노드의 개수일 때, depth 를 최소화하여 시간 복잡도를 줄이는 것이 핵심 아이디어이다. 동일한 노드의 개수일 때, depth 가 최소가 되는 경우는 tree 가 complete binary tree 인 경우이다.

Red-Black Tree 의 정의
Red-Black Tree 는 다음의 성질들을 만족하는 BST 이다.

각 노드는 Red or Black이라는 색깔을 갖는다.
Root node 의 색깔은 Black이다.
각 leaf node 는 black이다.
어떤 노드의 색깔이 red라면 두 개의 children 의 색깔은 모두 black 이다.
각 노드에 대해서 노드로부터 descendant leaves 까지의 단순 경로는 모두 같은 수의 black nodes 들을 포함하고 있다. 이를 해당 노드의 Black-Height라고 한다. cf) Black-Height: 노드 x 로부터 노드 x 를 포함하지 않은 leaf node 까지의 simple path 상에 있는 black nodes 들의 개수
Red-Black Tree 의 특징
Binary Search Tree 이므로 BST 의 특징을 모두 갖는다.
Root node 부터 leaf node 까지의 모든 경로 중 최소 경로와 최대 경로의 크기 비율은 2 보다 크지 않다. 이러한 상태를 balanced 상태라고 한다.
노드의 child 가 없을 경우 child 를 가리키는 포인터는 NIL 값을 저장한다. 이러한 NIL 들을 leaf node 로 간주한다.
RBT 는 BST 의 삽입, 삭제 연산 과정에서 발생할 수 있는 문제점을 해결하기 위해 만들어진 자료구조이다. 이를 어떻게 해결한 것인가?

삽입

우선 BST 의 특성을 유지하면서 노드를 삽입을 한다. 그리고 삽입된 노드의 색깔을 RED 로 지정한다. Red 로 지정하는 이유는 Black-Height 변경을 최소화하기 위함이다. 삽입 결과 RBT 의 특성 위배(violation)시 노드의 색깔을 조정하고, Black-Height 가 위배되었다면 rotation 을 통해 height 를 조정한다. 이러한 과정을 통해 RBT 의 동일한 height 에 존재하는 internal node 들의 Black-height 가 같아지게 되고 최소 경로와 최대 경로의 크기 비율이 2 미만으로 유지된다.

삭제

삭제도 삽입과 마찬가지로 BST 의 특성을 유지하면서 해당 노드를 삭제한다. 삭제될 노드의 child 의 개수에 따라 rotation 방법이 달라지게 된다. 그리고 만약 지워진 노드의 색깔이 Black 이라면 Black-Height 가 1 감소한 경로에 black node 가 1 개 추가되도록 rotation 하고 노드의 색깔을 조정한다. 지워진 노드의 색깔이 red 라면 Violation 이 발생하지 않으므로 RBT 가 그대로 유지된다.

Java Collection 에서 ArrayList 도 내부적으로 RBT 로 이루어져 있고, HashMap 에서의 Separate Chaining에서도 사용된다. 그만큼 효율이 좋고 중요한 자료구조이다.

Hash Table

데이터저장-자료구조-종류-해시테이블-해시함수-고유key인덱스생성

• HASH는 내부적으로 배열로 데이터 저장 -> 빠른 검색 속도를 갖음.
• 특정 값 검색시 -> 데이터 고유의 인덱스로 접근해 average case는 Time Complexity 가 O(1)이 됨. (항상 O(1)이 아니고 average case O(1)인 collision 발생시)
• 문제 : 인덱스로 저장되는 key값이 불규칙해서 특별한 알고리즘(해시 함수) 을 이용하여 저장할 데이터와 연관된 고유한 숫자를 만들어 낸 뒤 이를 인덱스로 사용.
• 특징 : 특정 데이터가 저장되는 인덱스는 그 데이터만의 고유한 위치이기 때문에, 삽입 연산 시 다른 데이터의 사이에 끼어들거나, 삭제시 다른 데이터로 채울 필요가 없어 산에서 추가적인 비용이 없도록 만들어진 구조.

고유key인덱스생성-returns hashcode-problem-same key creation-collision

• 고유한 인덱스 값을 생성.
• 반환된 데이터의 고유 숫자 값을 hashcode라고 함.
• 저장되는 값들의 key 값을 hash function을 통해서 작은 범위의 값들로 바꿔준다.
• 단 어설픈 hash function을 통해서 key 값들을 결정한다면 동일한 값이 도출될 수 있다. 이렇게 되면 동일한 key 값에 복수 개의 데이터가 하나의 테이블에 존재하게 되는데 이곳에 저장하려 하면 Collision이 발생함.

same key creation-collision-예방조건-필요한 이유

• 일반적으로 좋은 해시 함수는 키의 일부분을 참조하여 해쉬 값을 만들지 않고 키 전체를 참조하여 해쉬 값을 만든다.
• 하지만 좋은 해쉬 함수는 키가 어떤 특성을 가지고 있느냐에 따라 달라지게 된다.
• 해시 함수는 무조건 1:1 로 만드는 것보다 Collision 을 최소화하는 방향으로 설계하고 발생하는 Collision 에 대비해 어떻게 대응할 것인가가 더 중요.
• 1:1 대응이 되도록 만드는 것이 거의 불가능하기도 하지만 그런 hash function를 만들어봤자 그건 array 와 다를바 없고 메모리를 너무 차지하게 된다.
• Collision 이 많아질 수록 Search 에 필요한 Time Complexity 가 O(1)에서 O(n)에 가까워진다.
• 어설픈 hash function는 hash 를 hash 답게 사용하지 못하도록 한다.
• 좋은 hash function를 선택하는 것은 hash table 의 성능 향상에 필수적인 것이다.
• 따라서 hashing 된 인덱스에 이미 다른 값이 들어 있다면 새 데이터를 저장할 다른 위치를 찾은 뒤에야 저장할 수 있는 것이다. 따라서 충돌 해결은 필수.

해시충돌(collision-해결방법)

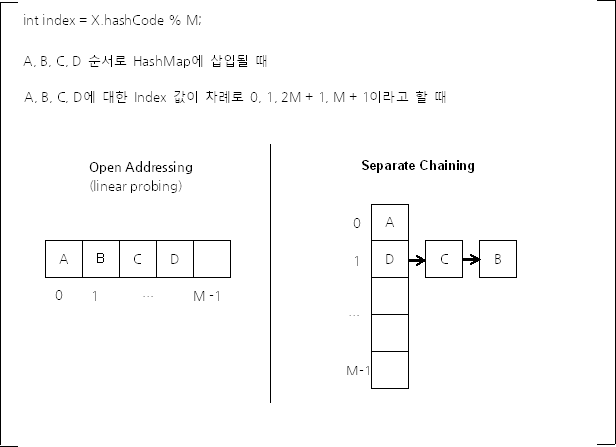
해시충돌-해결방법-Open Address방식(개방주소법)

• 해시 충돌이 발생하면, (즉 삽입하려는 해시 버킷이 이미 사용 중인 경우) 다른 해시 버킷에 해당 자료를 삽입하는 방식.
• 버킷이란 바구니와 같은 개념으로 데이터를 저장하기 위한 공간이라고 생각하면 된다. 다른 해시 버킷이란 어떤 해시 버킷을 말하는 것인가?
• 공개 주소 방식이라고도 불리는 이 알고리즘은 Collision 이 발생하면 데이터를 저장할 장소를 찾아 헤맨다.
• Worst Case 의 경우 비어있는 버킷을 찾지 못하고 탐색을 시작한 위치까지 되돌아 올 수 있다. 이 과정에서도 여러 방법들이 존재하는데, 다음 세 가지에 대해 알아보자.
• 1 Linear Probing 순차적으로 탐색하며 비어있는 버킷을 찾을 때까지 계속 진행된다.
• 2 Quadratic probing 2 차 함수를 이용해 탐색할 위치를 찾는다.
• 3 Double hashing probing 하나의 해쉬 함수에서 충돌이 발생하면 2 차 해쉬 함수를 이용해 새로운 주소를 할당한다. 위 두 가지 방법에 비해 많은 연산량을 요구하게 된다.

해시충돌-해결방법-Separate Chaining 방식(분리 연결법)

• 일반적으로 Open Addressing 은 Separate Chaining 보다 느리다.
• Open Addressing 의 경우 해시 버킷을 채운 밀도가 높아질수록 Worst Case 발생 빈도가 더 높아져서이다.
• 반면 Separate Chaining 방식의 경우 해시 충돌이 잘 발생하지 않도록 보조 해시 함수를 통해 조정할 수 있다면 Worst Case 에 가까워 지는 빈도를 줄일 수 있다.
• Java 7 에서는 Separate Chaining 방식을 사용하여 HashMap 을 구현하고 있다.
• Separate Chaining 방식으로는 두 가지 구현 방식이 존재한다.
• 연결 리스트를 사용하는 방식(Linked List)
• 각각의 버킷(bucket)들을 연결리스트(Linked List)로 만들어 Collision 이 발생하면 해당 bucket 의 list 에 추가하는 방식이다.
• 연결 리스트의 특징을 그대로 이어받아 삭제 또는 삽입이 간단하다.
• 하지만 단점도 그대로 물려받아 작은 데이터들을 저장할 때 연결 리스트 자체의 오버헤드가 부담이 된다.
• 또 다른 특징으로는, 버킷을 계속해서 사용하는 Open Address 방식에 비해 테이블의 확장을 늦출 수 있다.

해시충돌-해결방법-트리사용(Red-Black Tree)

• 기본적인 알고리즘은 Separate Chaining 방식과 동일하며 연결 리스트 대신 트리를 사용하는 방식이다.

• 연결 리스트를 사용할 것인가와 트리를 사용할 것인가에 대한 기준은 하나의 해시 버킷에 할당된 key-value 쌍의 개수이다.

• 데이터의 개수가 적다면 링크드 리스트를 사용하는 것이 맞다. 트리는 기본적으로 메모리 사용량이 많기 때문이다.

• 데이터 개수가 적을 때 Worst Case 를 살펴보면 트리와 링크드 리스트의 성능 상 차이가 거의 없다.

• 따라서 메모리 측면을 봤을 때 데이터 개수가 적을 때는 링크드 리스트를 사용한다.
  데- 이터가 적다는 것은 얼마나 적다는 것을 의미하는가?

• 앞에서 말했듯이 기준은 하나의 해시 버킷에 할당된 key-value 쌍의 개수이다.

• 이 키-값 쌍의 개수가 6 개, 8 개를 기준으로 결정한다. 기준이 두 개 인것이 이상하게 느껴질 수 있다. 7 은 어디로 갔는가?

• 링크드 리스트의 기준과 트리의 기준을 6 과 8 로 잡은 것은 변경하는데 소요되는 비용을 줄이기 위함이다.

• 한 가지 상황을 가정해보자. 해시 버킷에 6 개 의 key-value 쌍이 들어있었다. 그리고 하나의 값이 추가되었다.

• 만약 기준이 6 과 7 이라면 자료구조를 링크드 리스트에서 트리로 변경해야 한다. 그러다 바로 하나의 값이 삭제된다면 다시 트리에서 링크드 리스트로 자료구조를 변경해야 한다.

• 각각 자료구조로 넘어가는 기준이 1 이라면 Switching 비용이 너무 많이 필요하게 되는 것이다. 그래서 2 라는 여유를 남겨두고 기준을 잡아준 것이다.

• 따라서 데이터의 개수가 6 개에서 7 개로 증가했을 때는 링크드 리스트의 자료구조를 취하고 있을 것이고 8 개에서 7 개로 감소했을 때는 트리의 자료구조를 취하고 있을 것이다.

Open Address vs Separate Chaining

일단 두 방식 모두 Worst Case 에서 O(M)이다. 하지만 Open Address방식은 연속된 공간에 데이터를 저장하기 때문에 Separate Chaining에 비해 캐시 효율이 높다. 따라서 데이터의 개수가 충분히 적다면 Open Address방식이 Separate Chaining보다 더 성능이 좋다. 한 가지 차이점이 더 존재한다. Separate Chaining방식에 비해 Open Address방식은 버킷을 계속해서 사용한다. 따라서 Separate Chaining 방식은 테이블의 확장을 보다 늦출 수 있다.

보조 해시 함수
보조 해시 함수(supplement hash function)의 목적은 key의 해시 값을 변형하여 해시 충돌 가능성을 줄이는 것이다. Separate Chaining 방식을 사용할 때 함께 사용되며 보조 해시 함수로 Worst Case 에 가까워지는 경우를 줄일 수 있다.

해시 버킷 동적 확장(Resize)

해시 버킷의 개수가 적다면 메모리 사용을 아낄 수 있지만 해시 충돌로 인해 성능 상 손실이 발생한다. 그래서 HashMap 은 key-value 쌍 데이터 개수가 일정 개수 이상이 되면 해시 버킷의 개수를 두 배로 늘린다. 이렇게 늘리면 해시 충돌로 인한 성능 손실 문제를 어느 정도 해결할 수 있다. 또 애매모호한 '일정 개수 이상'이라는 표현이 등장했다. 해시 버킷 크기를 두 배로 확장하는 임계점은 현재 데이터 개수가 해시 버킷의 개수의 75%가 될 때이다. 0.75라는 숫자는 load factor 라고 불린다.

Reference
http://d2.naver.com/helloworld/831311

Graph

Graph-Types-Search

정점과 간선의 집합, Graph
cf) 트리 또한 그래프이며, 그 중 사이클이 허용되지 않는 그래프를 말한다.

그래프 관련 용어 정리
Undirected Graph 와 Directed Graph (Digraph)
말 그대로 정점과 간선의 연결관계에 있어서 방향성이 없는 그래프를 Undirected Graph 라 하고, 간선에 방향성이 포함되어 있는 그래프를 Directed Graph 라고 한다.

Directed Graph (Digraph)
V = {1, 2, 3, 4, 5, 6}
E = {(1, 4), (2,1), (3, 4), (3, 4), (5, 6)}
(u, v) = vertex u에서 vertex v로 가는 edge
Undirected Graph
V = {1, 2, 3, 4, 5, 6}
E = {(1, 4), (2,1), (3, 4), (3, 4), (5, 6)}
(u, v) = vertex u와 vertex v를 연결하는 edge

Degree

Undirected Graph 에서 각 정점(Vertex)에 연결된 Edge 의 개수를 Degree 라 한다. Directed Graph 에서는 간선에 방향성이 존재하기 때문에 Degree 가 두 개로 나뉘게 된다. 각 정점으로부터 나가는 간선의 개수를 Outdegree 라 하고, 들어오는 간선의 개수를 Indegree 라 한다.

가중치 그래프(Weight Graph)와 부분 그래프(Sub Graph)
가중치 그래프란 간선에 가중치 정보를 두어서 구성한 그래프를 말한다. 반대의 개념인 비가중치 그래프 즉, 모든 간선의 가중치가 동일한 그래프도 물론 존재한다. 부분 집합과 유사한 개념으로 부분 그래프라는 것이 있다. 부분 그래프는 본래의 그래프의 일부 정점 및 간선으로 이루어진 그래프를 말한다.

그래프를 구현하는 두 방법

인접 행렬 (adjacent matrix) : 정방 행렬을 사용하는 방법
해당하는 위치의 value 값을 통해서 vertex 간의 연결 관계를 O(1) 으로 파악할 수 있다. Edge 개수와는 무관하게 V^2 의 Space Complexity 를 갖는다. Dense graph 를 표현할 때 적절할 방법이다.

인접 리스트 (adjacent list) : 연결 리스트를 사용하는 방법
vertex 의 adjacent list 를 확인해봐야 하므로 vertex 간 연결되어있는지 확인하는데 오래 걸린다. Space Complexity 는 O(E + V)이다. Sparse graph 를 표현하는데 적당한 방법이다.

그래프 탐색

그래프는 정점의 구성 뿐만 아니라 간선의 연결에도 규칙이 존재하지 않기 때문에 탐색이 복잡하다. 따라서 그래프의 모든 정점을 탐색하기 위한 방법은 다음의 두 가지 알고리즘을 기반으로 한다.

깊이 우선 탐색 (Depth First Search: DFS)

그래프 상에 존재하는 임의의 한 정점으로부터 연결되어 있는 한 정점으로만 나아간다라는 방법을 우선으로 탐색한다. 일단 연결된 정점으로 탐색하는 것이다. 연결할 수 있는 정점이 있을 때까지 계속 연결하다가 더이상 연결되지 않은 정점이 없으면 바로 그 전 단계의 정점으로 돌아가서 연결할 수 있는 정점이 있는지 살펴봐야 할 것이다. 갔던 길을 되돌아 오는 상황이 존재하는 미로찾기처럼 구성하면 되는 것이다. 어떤 자료구조를 사용해야할까? 바로 Stack 이다. Time Complexity : O(V+E) … vertex 개수 + edge 개수

너비 우선 탐색 (Breadth First Search: BFS)

그래프 상에 존재하는 임의의 한 정점으로부터 연결되어 있는 모든 정점으로 나아간다. Tree 에서의 Level Order Traversal 형식으로 진행되는 것이다. BFS 에서는 자료구조로 Queue 를 사용한다. 연락을 취할 정점의 순서를 기록하기 위한 것이다. 우선, 탐색을 시작하는 정점을 Queue 에 넣는다.(enqueue) 그리고 dequeue 를 하면서 dequeue 하는 정점과 간선으로 연결되어 있는 정점들을 enqueue 한다. 즉 vertex 들을 방문한 순서대로 queue 에 저장하는 방법을 사용하는 것이다. Time Complexity : O(V+E) … vertex 개수 + edge 개수 ! BFS 로 구한 경로는 최단 경로이다.

Minimum Spanning Tree

그래프 G 의 spanning tree 중 edge weight 의 합이 최소인 spanning tree를 말한다. 여기서 말하는 spanning tree란 그래프 G 의 모든 vertex 가 cycle 이 없이 연결된 형태를 말한다.

Kruskal Algorithm

초기화 작업으로 edge 없이 vertex 들만으로 그래프를 구성한다. 그리고 weight 가 제일 작은 edge 부터 검토한다. 그러기 위해선 Edge Set 을 non-decreasing 으로 sorting 해야 한다. 그리고 가장 작은 weight 에 해당하는 edge 를 추가하는데 추가할 때 그래프에 cycle 이 생기지 않는 경우에만 추가한다. spanning tree 가 완성되면 모든 vertex 들이 연결된 상태로 종료가 되고 완성될 수 없는 그래프에 대해서는 모든 edge 에 대해 판단이 이루어지면 종료된다. Kruskal Algorithm의 세부 동작과정 Kruskal Algorithm 관련 Code

어떻게 cycle 생성 여부를 판단하는가?

Graph 의 각 vertex 에 set-id라는 것을 추가적으로 부여한다. 그리고 초기화 과정에서 모두 1~n 까지의 값으로 각각의 vertex 들을 초기화 한다. 여기서 0 은 어떠한 edge 와도 연결되지 않았음을 의미하게 된다. 그리고 연결할 때마다 set-id를 하나로 통일시키는데, 값이 동일한 set-id 개수가 많은 set-id 값으로 통일시킨다.

Time Complexity

Edge 의 weight 를 기준으로 sorting - O(E log E)
cycle 생성 여부를 검사하고 set-id 를 통일 - O(E + V log V) => 전체 시간 복잡도 : O(E log E)

Prim Algorithm

초기화 과정에서 한 개의 vertex 로 이루어진 초기 그래프 A 를 구성한다. 그리고나서 그래프 A 내부에 있는 vertex 로부터 외부에 있는 vertex 사이의 edge 를 연결하는데 그 중 가장 작은 weight 의 edge 를 통해 연결되는 vertex 를 추가한다. 어떤 vertex 건 간에 상관없이 edge 의 weight 를 기준으로 연결하는 것이다. 이렇게 연결된 vertex 는 그래프 A 에 포함된다. 위 과정을 반복하고 모든 vertex 들이 연결되면 종료한다.

Time Complexity
=> 전체 시간 복잡도 : O(E log V)

출처

https://github.com/JaeYeopHan/Interview_Question_for_Beginner
https://velog.io/@760kry/JS-Linked-List-vs-Array-List-data-structor