혼공학습단 2주차 미션을 준비하면서 일정표를 다시 확인해보았는데, 뭔가 이상하다.
챕터2개의 진도를 뺏던 지난주와는 다르게 챕터 1개만 되어있다.
다시 책을 확인해보니 책이 총 9챕터로, 뒤의 2개의 챕터는 딥러닝 심화 내용이라 혼공학습단 진도에서 빠진 것 같다. 그래도 혼공학습단 기간이 끝나도 끝까지 마무리 할 수 있도록 달려봐야겠다.(과연?)

제가 책을 보며 작업한 소스코드는 깃허브로 공유하겠습니다.
3장 깃허브

Chpater 03. 회귀 알고리즘과 모델 규제

03-1 k-최근접 이웃 회귀

k-최근접 이웃 분류 알고리즘 복습

• 예측하려는 샘플에 가장 가까운 샘플 k개를 선택
• 이 샘플들의 클래스를 확인하여 다수 클래스를 새로운 샘플의 클래스로 예측
• 다수결로 분류 결과가 정해지므로, k는 홀수로 선택

k-최근접 이웃 회귀

• 아이디어는 분류와 동일
• 예측하려는 샘플에 가장 가까운 샘플 k개를 선택
• 수치를 예측하기 위해 샘플 k개의 평균을 계산한 값을 도출
• 근데 회귀 알고리즘은 굳이 k가 홀수일 필요가 있을지 궁금
• 분류 알고리즘에서 k가 홀수인 이유는, 샘플들을 통해 다수결 투표로 클래스를 정할 때 동점 상황을 방지하기 위함이었음을 생각하면 회귀 알고리즘에서는 k가 꼭 홀수일 필요는 없을 것 같다(개인적 생각)

결정계수($R^2$;R-squared)

• 회귀 모델의 성능을 평가하기 위한 지표
• $\displaystyle R^2 = 1 - \frac{\sum(y_i - \hat{y_i})^2}{\sum(y_i - \bar{y})^2}$
• $y_i$ : 타깃값,   $\hat{y_i}$ : 예측값  , $\bar{y}$ : 평균값
• 타깃이 평균 정도를 예측하는 수준이라면(즉, 분자와 분모가 비슷해진다면) $R^2$는 0에 가까워지고, 예측이 타깃에 가까워지면(분자가 0에 가까워지면) 1에 가까운 값이 됨
• 즉, 1에 가까울수록 회귀 모델의 성능이 좋다고 할 수 있다

MAE(Mean Absolute Error)

• 회귀 모델의 성능을 평가하기 위한 지표
• $\displaystyle MAE = \frac{1}{n} \sum|y_i - \hat{y_i}|$
• $y_i$ : 타깃값,   $\hat{y_i}$ : 예측값 (용어 통일을 위해 위와 맞춰서 작성했는데, 확인중)
• 타깃과 예측의 절댓값 오차를 평균한 값이므로 값이 작을 수록 회귀 모델의 성능이 좋다고 할 수 있다

과소적합 vs 과대적합

• 과대적합 : 훈련 세트에서 점수가 좋았는데 테스트 세트에서 점수가 나쁜 경우
• 과소적합 : 훈련 세트보다 테스트 세트의 점수가 높거나 두 점수가 모두 너무 낮은 경우

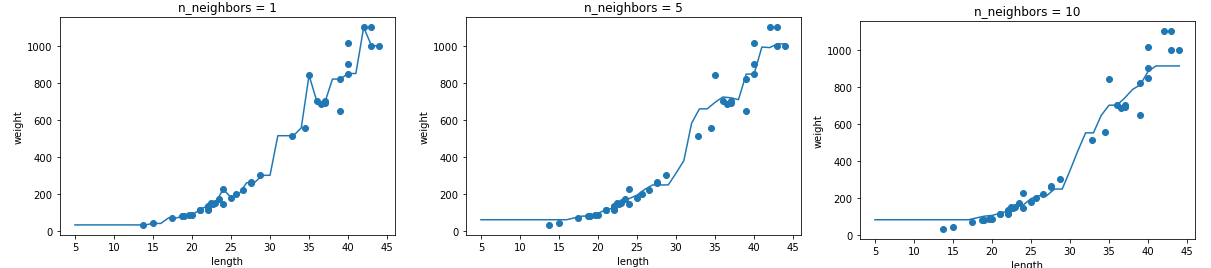
[2주차 기본미션에 대해 풀고 가겠습니다.]

3장 깃허브의 기본미션 부분의 소스코드가 있습니다.

03-2 선형 회귀

선형 회귀

• 회귀 알고리즘으로 데이터를 잘 대변할 수 있는 최적의 선을 찾는 모델
• sklearn.linear_model 패키지 아래의 LinearRegrssion 클래스로 구현되어 있음
  • 다항회귀 : 다항식을 사용한 선형회귀

모델 기반 학습 vs 사례 기반 학습

• 선형 회귀 알고리즘의 경우 coef(계수)와 intercept(절편) 값, 즉 모델 파라미터를 찾아내는 과정이지만, KNN 알고리즘의 경우 모델 파라미터 없이 훈련 세트를 저장하는 것이 훈련의 전부임
• 전자를 모델 기반 학습이라하고, 후자를 사례 기반 ㅎ학습이라고 함

[2주차 선택미션에 대해 풀고 가겠습니다.]

• 모델 파라미터란?
• 선형 회귀가 찾은 가중치처럼 머신러닝 모델이 특성에서 학습한 파라미터

03-2 특성 공학과 규제

다중 회귀

• 여러 개의 특성을 사용한 선형 회귀
• 특성이 많은 고차원에서 선형 회귀가 복잡한 모델 표현 가능

특성 공학(feature engineering)

• 특성 공학하면 뭔가 이상하다..피처 엔지니어링이라 하자....
• 기존의 특성을 사용해 새로운 특성을 뽑아내는 작업

규제(Regularization)

• 머신러닝 모델이 훈련 세트를 너무 과도하게 학습하지 못하도록 제한하는 것
• 모델이 훈련 세트에 과대적합되지 않도록 하는 것
• 선형 회귀 모델의 경우 특성에 곱해지는 계수(또는 기울기)의 크기를 작게 만드는 것

릿지 회귀(Ridge)

• sklearn.linear_model의 Ridge 클래스 구현되어 있음
• 릿지는 규제의 양을 조절할 때 alpha 매개변수를 통해 강도를 조절
• alpha가 크면 규제의 강도가 세지므로 계수 값을 더 줄이고, 과소적합되도록 유도
• alpha가 작으면 계수를 줄이는 역할로 과대적합 가능성 증가

라쏘 회귀(Lasso)

• sklearn.linear_model의 Lasso 클래스 구현되어 있음
• 릿지는 규제의 양을 조절할 때 alpha 매개변수를 통해 강도를 조절
• alpha가 크면 규제의 강도가 세지므로 계수 값을 더 줄이고, 과소적합되도록 유도
• alpha가 작으면 계수를 줄이는 역할로 과대적합 가능성 증가

하이퍼파라미터란?

• 머신러닝 알고리즘이 학습하지 않는 파라미터로, 사람이 사전에 지정해야 한다.
• 릿지와 라쏘 회귀의 alpha와 같은 값이 하이퍼파라미터이다