https://jurogrammer.tistory.com/133?category=959000 를 공부하고 참조하여 작성함.

Lambda Calculus

• formal system, computation 표현하기 위한 mathmetical logic.
• function의 추상화 형태.
• variable을 연결/치환함으로써 함수에 적용.

Notation

• lambda calculus에서 유효한 표기법

Lambda terms

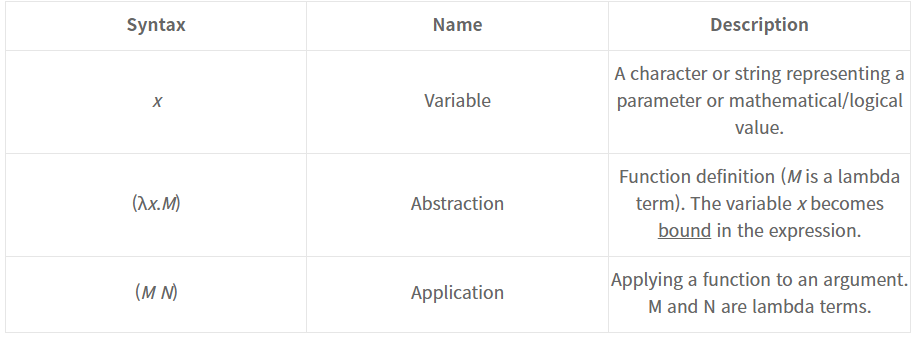
1. Value: 변수. parameter 혹은 수학,논리적 value를 의미. (수학: 1,2,3 / 논리학: 참,거짓)
2. Abstraction: 함수를 정의 한 것.

• (λx.M)표기 : 함수(λ)인데, x를 집어넣으면 M을 반환(또는 치환, 변환)
  (ex) f(x) = x^2 + 2를 Abstraction 표기법? -> x는 fx(x)의 x에 해당. M은 x^2+2에 해당.

3. Application

• function에 Lambda를 집어넣는 것.
  (ex) f(x) = x^2 + 2에 2를 대입 -> (λx.x^2+2) (2)

# x=2 대입
function (x):
	return x^2+2	

• lambda calculus에는 변수 선언이 존재 X-> λx.x+y : input인 x를 집어넣으면 x에 아직 알려지지 않은 y를 더한다

Operation

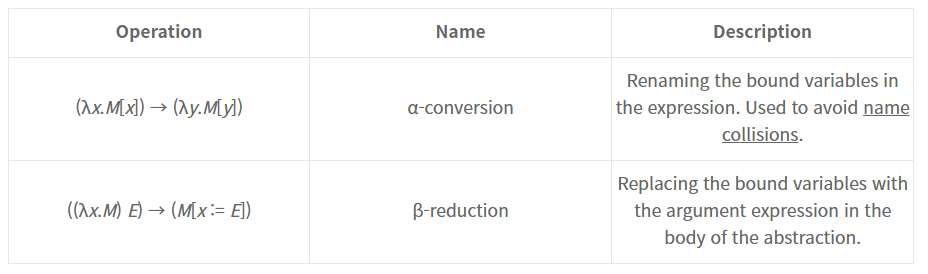
1. α-conversion

• 단순히 변수 명만 바꿔 주는 것. 의미는 동일
• f(x) = x^2 + 2로 표기하나 f(t) = t^2 + 2로 표기하나 함수의 동작방식면에선 차이가 없음.
• λx.x^2+2의 x와 λx.x+2의 x는 서로 다른 x인데, operation할 때 혼동 가능성이 존재. 따라서 name collision을 피하기 위해 다른 변수로 치환 (α-conversion)

2. β-reduction

• 쉽게 말해서, f(x) = x^2 + 2 함수에서 2를 대입한 식 f(2) = 2^2 + 2를 β-reduction 이라고 함.
• ((λx.M) E)이렇게 적으면, (M[x := E])로 됨. 즉 M에 E를 대입한 것
• (λx.x^2+2) (2) 라는 2개의 lambda terms가 λx.x^2+2[x:=2]또는 6이라고 1개의 lambda terms로 줄어든다. (β-reduction)

• 추가로 알아야 할 사항

Free variables

• λx.x^2+2 ->x는 x^2 + 2에 관해 binding 됐다고 할 수 있음. 이와 반대로 free variables도 존재.
• Free variables의 정의

  1. lambda terms인 variable x만 본다면, x 그 자체가 free variable\
  2. λx.t의 free variable 집합은 t의 free variables 집합. but x는 제외
  3. ts의 free variable 집합은 t의 free variable 집합과 s의 free variable 집합의 합집합입니다.

ex 1) λx.x
1. λx.x에서 우측 x는 정의 1번에 의해 free variable
2. lambda terms인 λx.x를 체크. 정이 2번을 적용한다면 t에 해당하는 x의 free variable은 x. 그리고 좌측 람다 옆의 변수 x를 제외. 따라서 {x} - {x} 해서 free variable은 없다! 라고 말할 수 있음.

ex 2) λx.yx
-> y가 free variables

Capture-avoiding substitutions

• 서로 다른 의미가 동일한 의미로 capturing되는 것을 피하기 위해 치환 (α-conversion과 관련)

brancket 사용(소괄호)

• 애매함을 제거하기 위해 사용

functions that operate on functions

• lambda calculus에서 함수는 first class values로 취급. 따라서 function이 input이 될수도, output이 될수도 있음.