https://www.youtube.com/watch?v=3VQ382QG-y4 강의와 https://jurogrammer.tistory.com/139?category=959000를 보고 작성한 글.

lambda calculus-> boolean으로 표현하기

β-reduction

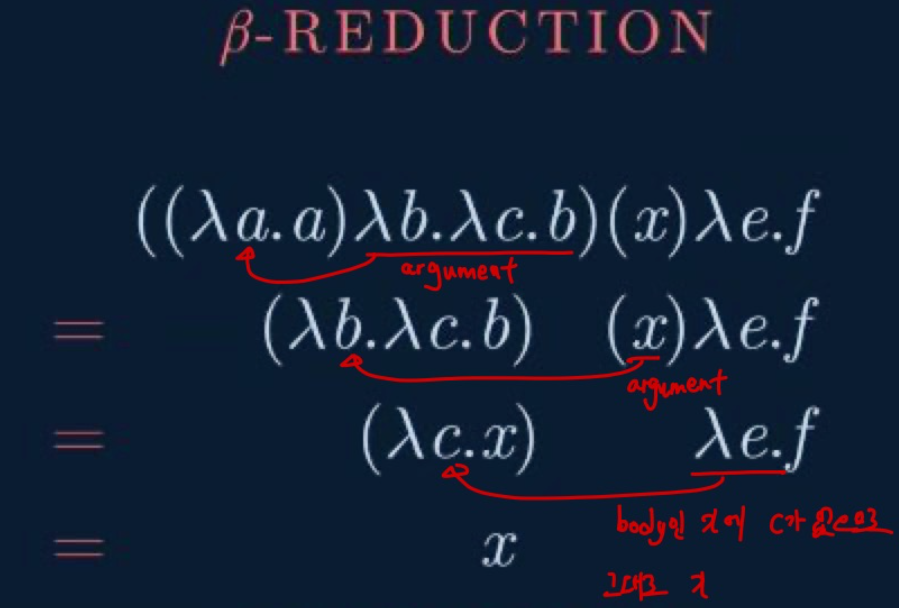
• 첫번째 reduction에서는 a를 인수로 받으면 그대로 a가 반환되는 abstraction. 그대로 λb.λc.b가 반환
• λb.λc.b는 b를 인수로 받아 λc.b를 반환하고, c인수를 받아 b를 반환하는 abstraction. x하나만 application을 한다면 λc.x가 반환.
• 인수 c를 받아 x를 반환하기 때문에 어떤 값을 넣어도 x를 반환함. body에 c에 관한 variable이 없기 때문 (bounded variable 존재X ). 따라서 λe.f를 λc.x에 applicatoin한다면 x가 반환됨.

함수의 종류

1. Idiot (I)

• a를 대입하면 a가 나옴.

I := λa.a

2. Mockingbird (M, ω, omegra)

• f를 입력하면, f에 f를 application하는 함수를 반환

M := λf.ff

M => f => f(f)

• M(I) => I(I) =>I
• M(M) =>M(M)..... 자기 자신을 무한히 application 함 (stack overflow 발생)

3. Kestrel (K)

• a,b 인수를 순차적으로 application하면 a를 반환하는 함수. 파라미터의 앞 부분만 반환 시킴.

K := λab.a
   = λa.λb.a

• K(I)(M) => I (앞의 것을 반환)
• K(K)(M) => K

4. Kite (K*)

K* := λab.b

• 위의 combinators 4가지로 boolean (True,False, And, or, Xor, not) 표현 가능.

Booleans 연산