자료구조: ch2) 자료구조 & 알고리즘의 시간복잡도/ Big O 표기법

시간복잡도란?

• 계산 복잡도 이론에서 시간 복잡도는 문제를 해결하는데 걸리는 시간과 입력의 함수 관계를 가리킨다. (https://ko.wikipedia.org/wiki/%EC%8B%9C%EA%B0%84_%EB%B3%B5%EC%9E%A1%EB%8F%84)

• 시간복잡도란 알고리즘이 문제를 해결하기 위한 시간(연산)의 횟수

• 알고리즘은 유한한 자원을 가진 환경에서 주어진 문제를 푸는 동작의 모임. 이때, 적은 시간과 적은 자원(공간)을 이용해 문제 해결하는 알고리즘이 좋은 알고리즘이라 할 수 있다.

• 연산 횟수를 줄여서 시간 복잡도를 줄이는 것이 이상적인 알고리즘

->알고리즘 수행시간= 최악의 입력에 대한 기본 연산 횟수

시간복잡도 Counting 방법

1. 전역 변수를 이용하여 Elmentary Operation(기본 연산)을 카운팅

2. 각 실행문 별로 Step수와 실행 횟수를 분석하고 계산한다.

Big O?

• T(n)으로 표현한 함수의 최고차항의 차수가 빅오가 된다. 보통 O(n^2) 이상의 복잡도를 가지는 알고리즘은 좋지 않다고 평가된다.

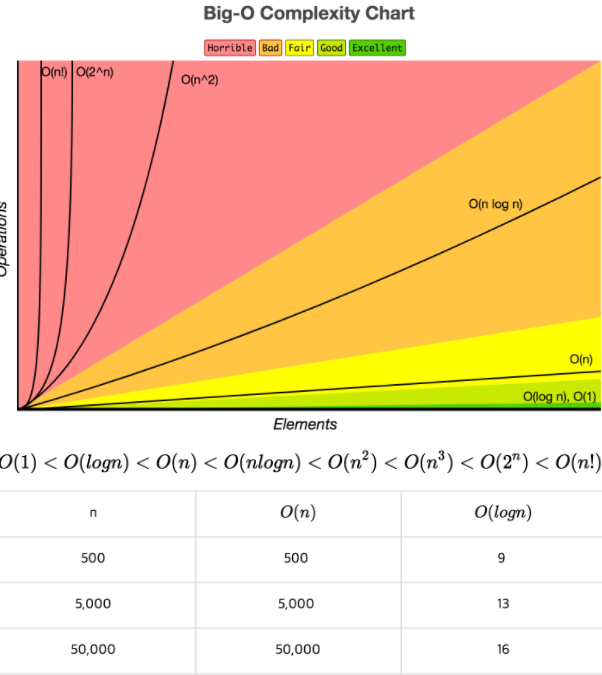
오른쪽으로 갈수록 난리가 나는 시간복잡도를 볼 수 있다.

def numberof-bits(n) 함수를 주목해서 공부하면 좋을 듯 해서 캡쳐해두었다.