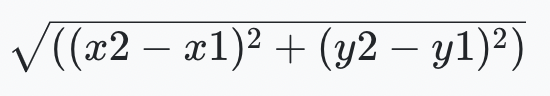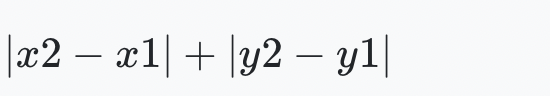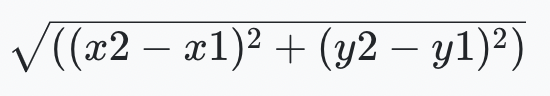키패드 누르기 [level 1] (두 점 사이의 거리 구하기)

# 1. 맨 처음 왼손 엄지 * 오른손 엄지 #
# 2. 엄지 손가락은 상하좌우 1칸씩 이동 가능
#3. 1,4,7은 왼손 엄지 (V)
#4. 3,6,9는 오른손 엄지 (V)
#5. 2,5,8,0 입력은 두 엄지 손가락 중 가까운 것 사용 (V)`
#5-1. 엄지 손가락 거리 같으면 오른손잡이->오른손 /왼손잡이->왼손
# 문제되는 부분은 2,5,8,0 입력시

def distance(dot1,dot2):
    distance=abs(dot1[0]-dot2[0])+abs(dot1[1]-dot2[1])
    return distance

def solution(numbers, hand):
    answer = ''
    hand_list=[]
    user_hand=hand

    #dic로 좌표 나타내기
    number_dic={1:(0, 0), 2:(0, 1), 3:(0, 2),
                4:(1, 0), 5:(1, 1), 6:(1, 2),
                7:(2, 0), 8:(2, 1), 9:(2, 2),
                '*':(3, 0), 0:(3, 1), '#':(3, 2)}


    left, right = set([1,4,7]), set([3,6,9]) # 왼쪽 숫자, 오른쪽 숫자
    middle=set([2,5,8,0]) # 중간 숫자
    now_l, now_r = '*', '#' # 손 위치 초기화

    for num in numbers:
        if num in left: # 왼쪽 키라인
            answer += 'L'
            now_l = num
        elif num in right: # 오른쪽 키라인
            answer += 'R'
            now_r = num
        else: # 미들 키 라인
            ld=distance(number_dic[num],number_dic[now_l])
            rd=distance(number_dic[num],number_dic[now_r])

            if ld>rd:
                answer+='R'
                now_r=num
            elif ld<rd:
                answer+='L'
                now_l=num
            elif ld==rd:
                if user_hand=='right':
                    answer+='R'
                    now_r=num

                else:
                    answer+='L'
                    now_l=num

    return answer

• 위치를 좌표로 나타내서 풀기
• 리스트 대신 문자열로 풀기
• [1,2,3,4] 대신 set([1,2,3,4]) = {1,2,3,4} (집합)
• distance=(dot1[0]-dot2[0])**2+(dot1[1]-dot2[1])**2
  대신
  distance=abs(dot1[0]-dot2[0])+abs(dot1[1]-dot2[1])
  사용하니 풀림. 이유는 모르겟음
  -> 이유는 https://velog.io/@jinyongp/Algorithm-%ED%94%84%EB%A1%9C%EA%B7%B8%EB%9E%98%EB%A8%B8%EC%8A%A4-%ED%82%A4%ED%8C%A8%EB%93%9C-%EB%88%84%EB%A5%B4%EA%B8%B0 있음

거리 공식

• 맨해튼 거리: 대각선이 아닌 상하좌우로 이동할 때 거리구하는 공식

  

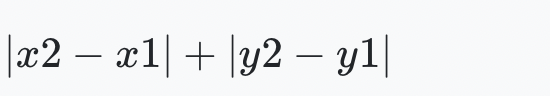
• 유클리드 거리: 유클리드 거리는 피타고라스 정리를 이용한 방법이다. (x1,y1) 위치의 점과 (x2,y2) 위치의 점 사이의 대각선 거리를 구할 때 사용